Sample Algebra I Final Exam Questions and Solutions
A printable Sample Final Exam (pdf document) for this entire Algebra I course is available here:
Sample Final Exam Questions: Algebra I
This web page contains written-out solutions to each of the questions.
Question 1: Renaming Expressions
Rename $\displaystyle\,\frac{1}{\sqrt 2}\,$ as a fraction with no radical in the denominator:
$$ \begin{align} \frac1{\sqrt 2} &= \frac1{\sqrt 2}\cdot \frac{\sqrt 2}{\sqrt 2}\cr\cr &= \frac{\sqrt 2}2 \end{align} $$Key concept: multiplying by $\,1\,$ changes the name of a number, but not where it ‘lives’ on a number line! Also, by definition of square roots, $\,\sqrt 2\cdot\sqrt 2 = 2\,.$
Lesson: Practice with Radicals
Rename $\,7\,$ as a quotient of integers, where the numerator is greater than $\,10\,$:
$$ \begin{align} 7 &= 7\cdot \frac 22\cr\cr &= \frac 71\cdot\frac 22\cr\cr &= \frac{14}2 \end{align} $$Many other answers are possible.
Rename $\,23{,}000{,}000\,$ in scientific notation:
$$ \begin{align} 23{,}000{,}000 &= 23{,}000{,}000\times \overbrace{10^{-7}\times 10^7}^{=\, 10^0\, =\, 1}\cr\cr &= (23{,}000{,}000 \times 10^{-7})\times 10^7\cr\cr &= 2.3 \times 10^7 \end{align} $$Rename $\,7\,$ in the form $\,x - y\,,$ where $\,x\,$ and $\,y\,$ are not integers:
$$ \begin{align} 7 &= 7 + \overbrace{(\frac 12 - \frac 12)}^{\text{add zero}}\cr\cr &= (7 + \frac 12) - \frac 12\cr\cr &= \frac{15}2 - \frac 12 \end{align} $$Many other answers are possible.
Key concept: adding $\,0\,$ changes the name of a number, but not where it ‘lives’ on a number line!
Rename $\,7\,$ in the form $\,\frac 12 x\,$:
$$ \begin{align} 7 &= \overbrace{\frac12 \cdot 2}^{=\,1}\,\cdot 7 \cr &\qquad \text{(bring $\,\frac 12\,$ into the picture)}\cr\cr &= \frac 12(14) \end{align} $$Rename $\,(x-2)(x+3)\,$ as a sum (i.e., multiply out):
$$ \begin{align} (x-2)(x+3) &= x\cdot x + 3x - 2x - 6\cr &\qquad \text{(using FOIL)}\cr\cr &= x^2 + x - 6 \end{align} $$FOIL stands for Firsts, Outers, Inners, Lasts.
Rename $\,x^2 - y^2\,$ as a product (i.e., factor):
$$ x^2 - y^2 = (x-y)(x+y) $$Rename $\displaystyle\,\frac 12\,$ in the form $\displaystyle\,\frac 3x\,$:
Approach #1: Multiply by $\,1\,$ in a form that brings $\,3\,$ into the picture:
$$ \frac 12 = \frac 12\cdot\frac 33 = \frac 36 $$Approach #2: Solve an equation:
$$ \begin{gather} \frac 12 = \frac 3x\cr\cr (2x)(\frac 12) = (2x)(\frac 3x)\cr\cr x = 6 \end{gather} $$So, $\,\frac 12 = \frac 36\,.$
Rename $\displaystyle\,\frac 1x - \frac 2{x+3}\,$ as a single fraction:
$$ \begin{align} &\frac 1x - \frac 2{x+3}\cr\cr &\quad = \frac 1x\cdot\frac{x+3}{x+3} - \frac 2{x+3}\cdot\frac{x}x\cr\cr &\quad = \frac{x+3}{x(x+3)} - \frac{2x}{x(x+3)}\cr\cr &\quad = \frac{x+3 - 2x}{x(x+3)}\cr\cr &\quad = \frac{-x + 3}{x(x+3)} = \frac{3-x}{x(x+3)} \end{align} $$Either of these final names is equally good!
Rename $\,0.25\,$ as a percent:
$$ \begin{align} 0.25 &= \frac{25}{100}\cr &= 25\cdot \frac 1{100}\cr &= 25\% \end{align} $$Lesson: Changing Decimals to Percent
Rename $\displaystyle\,\frac{x^4x^{-1}}{(x^2)^3 x}\,$ in the form $\,x^k\,$:
$$ \begin{align} \frac{x^4x^{-1}}{(x^2)^3 x} &= \frac{x^{4+(-1)}}{x^6x^1}\cr\cr &= \frac{x^3}{x^7}\cr\cr &= x^{3-7}\cr\cr &= x^{-4} \end{align} $$There are many other ways that this could be done.
Lesson: Multi-Step Exponent Law Practice
Rename $\,300\text{ ft/sec}\,$ in the form $\,x\,\text{ mph}\,.$ Here, ‘mph’ is ‘miles per hour’, and there are $\,5{,}280\,$ feet in one mile.
$$ \begin{align} 300\text{ ft/sec} &= \frac{300\text{ ft}}{\text{sec}}\cr\cr &= \frac{300 \text{ ft}}{\text{sec}}\cdot \frac{1\text{ mile}}{5280\text{ ft}}\cdot \frac{60\text{ sec}}{1\text{ min}}\cdot \frac{60\text{ min}}{1\text{ hr}}\cr\cr &= \frac{300(60)(60)\text{ miles}}{5280 \text{ hr}}\cr\cr &\approx 204.5 \text{ mph} \end{align} $$Lesson: Rate Problems
Question 2: Solving Mathematical Sentences (Equations, Inequalities, Compound Sentences)
Solve each equation/inequality in one variable. Write a list of equivalent sentences, ending with one that can be solved by inspection. Get exact answer(s), not decimal approximations. Graph each solution set on a number line.
Solve: $\,3x(1-5x)(x^2-16) = 0$
$$ \begin{gather} 3x(1-5x)(x^2-16) = 0\cr\cr 3x = 0\ \ \text{or}\ \ 1-5x = 0\ \ \text{or}\ \ x^2-16 = 0\cr\cr x = 0\ \ \text{or}\ \ 1 = 5x\ \ \text{or}\ \ x^2 = 16\cr\cr x = 0\ \ \ \text{or}\ \ \ x = \frac15\ \ \ \text{or}\ \ \ x = \pm 4 \end{gather} $$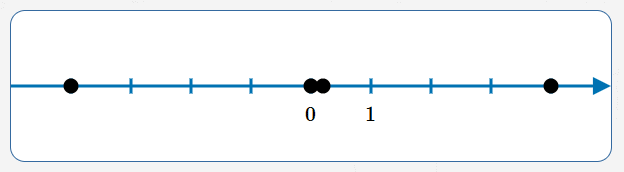
Key idea: recognize that a product equals zero, and use the Zero Factor Law. Recall that ‘$\,x=\pm 4\,$’ means ‘$\,x = 4\ \ \text{or}\ \ x = -4\,$’.
Solve: $\displaystyle\,\frac 12x - 7 = 3x + \frac x5$
$$ \begin{gather} \frac 12x - 7 = 3x + \frac x5\cr\cr 10(\frac 12x - 7) = 10(3x + \frac x5)\cr \text{(clear fractions)}\cr\cr 5x - 70 = 30x + 2x\cr\cr -27x = 70\cr\cr x = -\frac{70}{27} \approx -2.6 \end{gather} $$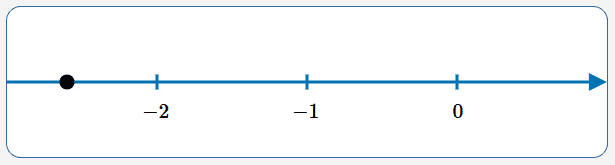
Solve: $\,|x-3|\gt 1$
$$ \begin{gather} |x-3|\gt 1\cr\cr x-3\gt 1\ \ \ \text{or}\ \ \ x-3 \lt -1\cr\cr x\gt 4\ \ \ \text{or}\ \ \ x\lt 2 \end{gather} $$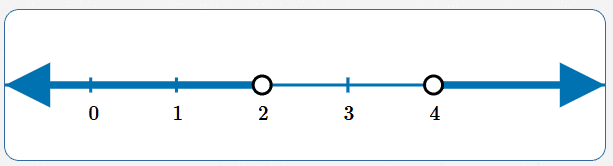
Lesson: Solving Absolute Value Inequalities Involving ‘Greater Than’
Advanced solution: if you've already learned that $\,|x-y|\,$ gives the distance between $\,x\,$ and $\,y\,,$ then this can be solved by inspection: we want all numbers $\,x\,$ whose distance from $\,3\,$ is greater than $\,1\,.$
Solve: $\,2\lt |x|\lt 3$
We want all numbers $\,x\,$ whose distance from $\,0\,$ is between $\,2\,$ and $\,3\,.$
$$ \begin{gather} 2\lt |x|\lt 3\cr\cr 2 \lt |x|\ \ \ \text{and}\ \ \ |x|\lt 3\cr\cr |x| \gt 2\ \ \ \text{and}\ \ \ |x|\lt 3 \end{gather} $$In other words, we want all numbers $\,x\,$ whose distance from $\,0\,$ is greater than $\,2\,$ and less than $\,3\,.$
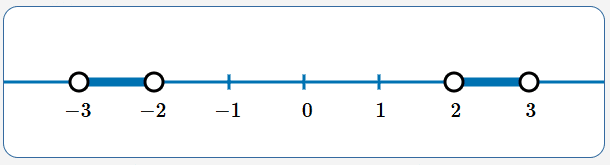
Lessons:
Simplifying Basic Absolute Value Expressions
Solving Absolute Value Inequalities Involving
‘Greater Than’
Solving Absolute Value Inequalities Involving ‘Less Than’
Solve: $\,1-2x\lt 3$
$$ \begin{gather} 1-2x\lt 3\cr\cr -2x\lt 2\cr\cr x\gt -1 \end{gather} $$Remember: when you multiply/divide both sides of an inequality by a negative number, you must change the direction of the inequality symbol!
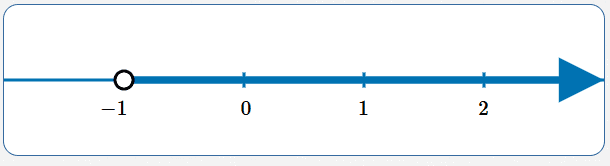
Lesson: Solving Simple Linear Inequalities with Integer Coefficients
Solve: $\,x^2 = x + 2$
$$ \begin{gather} x^2 = x + 2\cr\cr x^2 - x - 2 = 0\cr\cr (x-2)(x+1) = 0\cr\cr x = 2\ \ \ \text{or}\ \ \ x=-1 \end{gather} $$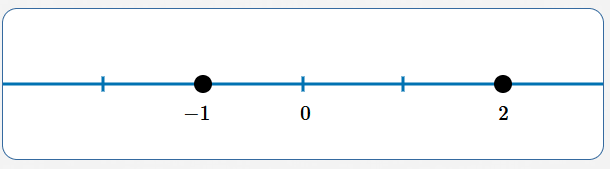
Solve: $\,1\lt x\ \ \ \text{or}\ \ \ x\le -1\,$
$$ \begin{gather} 1\lt x\ \ \ \text{or}\ \ \ x\le -1\cr\cr x\gt 1\ \ \ \text{or}\ \ \ x\le -1 \end{gather} $$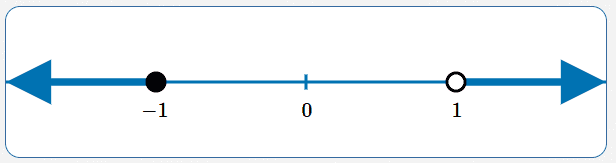
Lesson: Practice With the Mathematical Words ‘and’, ‘or’, ‘is equivalent to’
Solve: $\,0.005(x - 0.01) = 0.003 + 0.4x$
$$ \begin{gather} 0.005(x - 0.01) = 0.003 + 0.4x\cr\cr (1000)\bigl(0.005(x - 0.01)\bigr) = (1000)\bigl(0.003 + 0.4x\bigr)\cr\cr 5(x-0.01) = 3 + 400x\cr\cr 5x - 0.05 = 3 + 400x\cr\cr -395x = 3.05\cr\cr x = \frac{3.05}{-395} = -\frac{305}{39500} = -\frac{61}{7900} \approx -0.0077 \end{gather} $$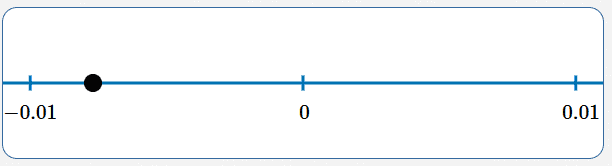
Question 3: Graphing Equations/
Graph each of the following equations/inequalities, where each sentence is viewed as a sentence in two variables. (That is, $\,x = 3\,$ should be viewed as $\,x + 0y = 3\,.$)
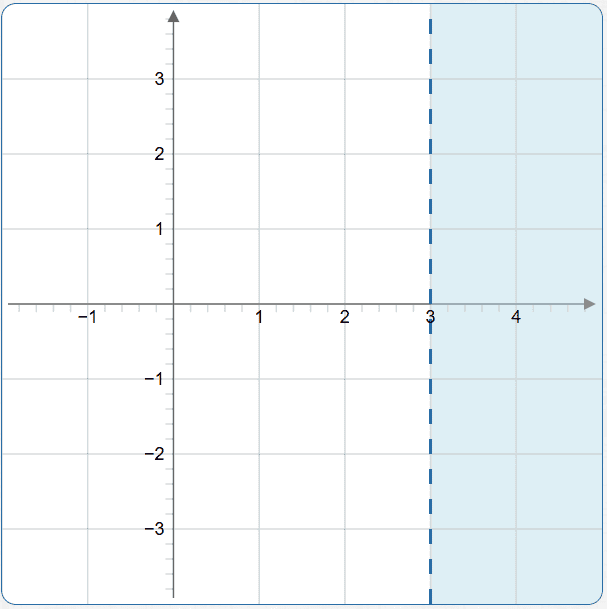
Graph $\,x\gt 3\,,$ viewed as an inequality in two variables.
We are viewing this as: $\,x + 0y \gt 3$
We want the set of all points $\,(x,y)\,,$ where $\,x\gt 3\,$ and $\,y\,$ is any real number. To show this set:
- Dash the vertical line $\,x = 3\,$ (to show that it is not included)
- Shade everything to the right
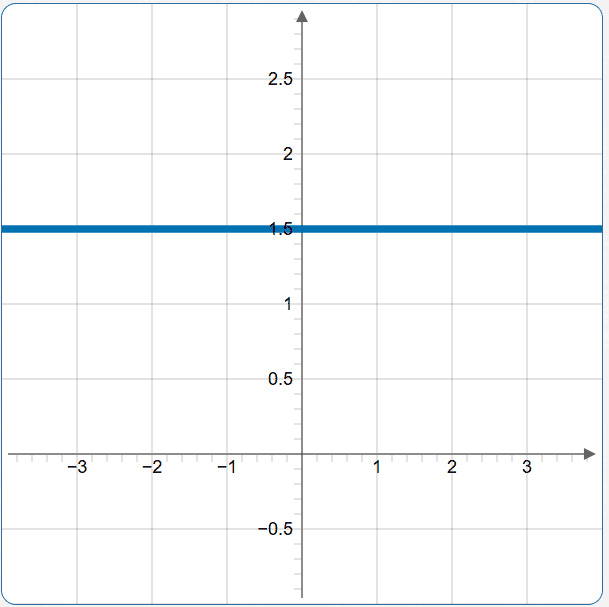
Graph $\,2y - 3 = 0\,,$ viewed as an equation in two variables.
We are viewing this as: $\,0x + 2y - 3 = 0$
$$ \begin{gather} 2y - 3 = 0\cr\cr 2y = 3\cr\cr y = \frac 32 \end{gather} $$We want the set of all points $\,(x,y)\,$ where $\,y = \frac 32\,$ and $\,x\,$ is any real number. This is the horizontal line that crosses the $y$-axis at $\,\frac 32\,$:
Lesson: Horizontal and Vertical Lines
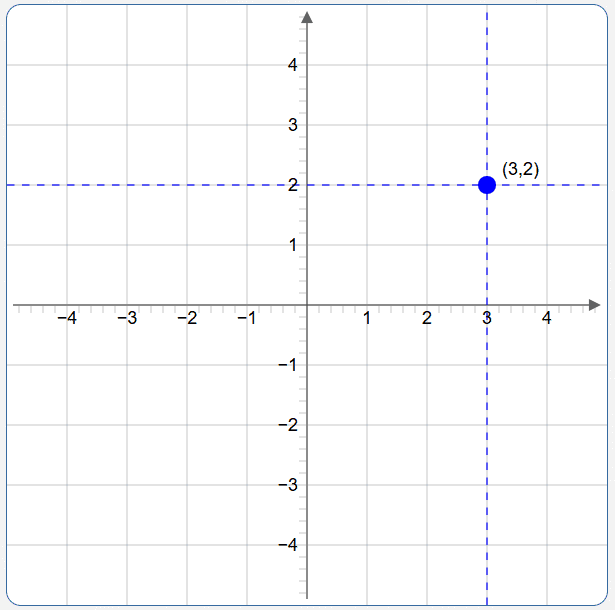
Graph the compound sentence: $\,x = 3\ \ \text{and}\ \ y = 2$
This is the mathematical word ‘and’.
It is the intersection of the vertical line $\,x = 3\,$ and the horizontal line $\,y = 2\,,$ which is the single point $\,(3,2)\,.$
Lessons:
Horizontal and Vertical Lines
Practice With the Mathematical Words
‘and’, ‘or’, ‘is equivalent to’
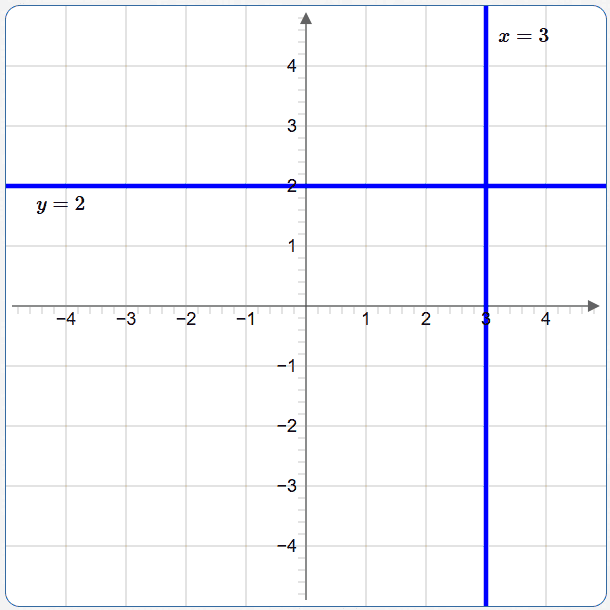
Graph the compound sentence: $\,x = 3\ \ \text{or}\ \ y = 2$
This is the mathematical word ‘or’.
It is the union of the vertical line $\,x = 3\,$ and the horizontal line $\,y = 2\,.$
Lessons:
Horizontal and Vertical Lines
Practice With the Mathematical Words
‘and’, ‘or’, ‘is equivalent to’
Graph the equation in two variables: $\,y = 2x - 1$
This is the line with slope $\,2\,$ that crosses the $y$-axis at $\,-1\,.$
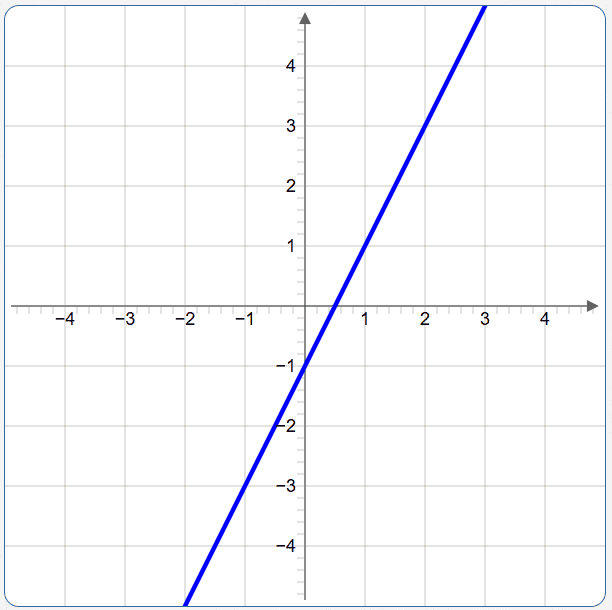
Lesson: Graphing Lines
Graph the equation in two variables: $\,y = \sqrt{x}$
Eventually, this will be one of the ‘basic models’ that you should have on your fingertips! For a first time, though, plot a few easy points, and see the shape that emerges:
| $x$ | $y$ |
| $0$ | $\sqrt{0} = 0$ |
| $1$ | $\sqrt{1} = 1$ |
| $4$ | $\sqrt{4} = 2$ |
| $9$ | $\sqrt{9} = 3$ |
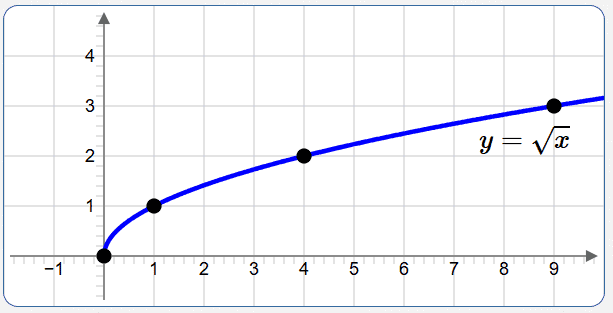
Lesson: Introduction to Equations and Inequalities in Two Variables
Graph the equation in two variables: $\,|x| = 2$
We are viewing this as: $\,|x| + 0y = 2$
Note that:
$$ \begin{gather} |x| = 2\cr \text{is equivalent to}\cr x = 2\ \ \text{or}\ \ x = -2 \end{gather} $$We need the set of all points $\,(x,y)\,$ for which $\,x = 2\,$ or $\,x = -2\,.$ Here, $\,y\,$ can be any real number. This is the union of two vertical lines:
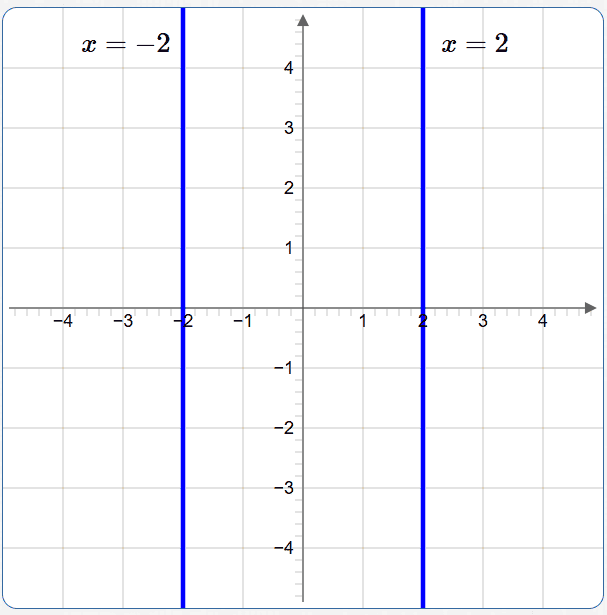
Graph the inequality in two variables: $\,y \le 2$
We are viewing this as: $\,0x + y \le 2$
We need the set of all points $\,(x,y)\,$ for which $\,y \le 2\,.$ Here, $\,x\,$ can be any real number. First, graph the horizontal line $\,y = 2\,,$ solid (showing that it is included in the solution set). Then, shade everything beneath this line:

Graph the equation in two variables: $\displaystyle\,\frac{y-2}3 = 2x - 1$
$$ \begin{gather} \frac{y-2}3 = 2x - 1\cr\cr y - 2 = 3(2x-1)\cr\cr y - 2 = 6x - 3\cr\cr y = 6x - 1 \end{gather} $$This is the line with slope $\,6\,$ that crosses the $y$-axis at $\,-1\,.$
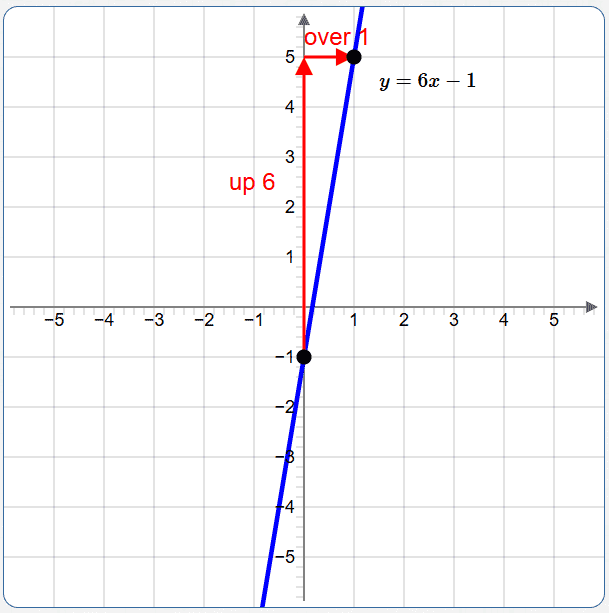
Question 4 (Order of Operation, Calculator Skills)
Estimate each of the following numbers on your calculator. For full credit, each answer must be correct to five decimal places.
Keystrokes differ depending on what type of calculator you are using.
Your aim should be to never key in an intermediate calculator result, since this can introduce computational error. Instead—as needed—store and recall results.
Evaluate $\,3x^2 - 5x + 1\,,$ where $\,x = -1.8\,$:
$$ 3(-1.8)^2 - 5(-1.8) + 1 = 19.72 $$Evaluate $|1 - 2x|\,,$ where $\,x = \sqrt 3\,$:
$$ |1-2(\sqrt 3)| \approx 2.46410 $$Questions 5, 6, and 7 assess understanding of the function concept, function notation, and graphing calculator skills.
Question 5
(a) What is the domain of the function $\displaystyle\,f(x) = \frac{1-3x}{x-2}\,$?
The domain of $\,f\,$ is the set of all real numbers $\,x\,$ for which the denominator is not zero. Therefore, only the number $\,2\,$ must be excluded from the domain.
Letting $\,\text{dom}(f)\,$ denote the domain of $\,f\,,$ using interval notation, and recalling that ‘$\,\cup\,$’ is the union operation, we have:
$$ \text{dom}(f) = (-\infty,2)\cup (2,\infty) $$(b) Use your graphing calculator to graph the function $\,f\,$ in the window $\,-1\lt x\lt 3\,$ and $\,-15\lt y\lt 10\,.$
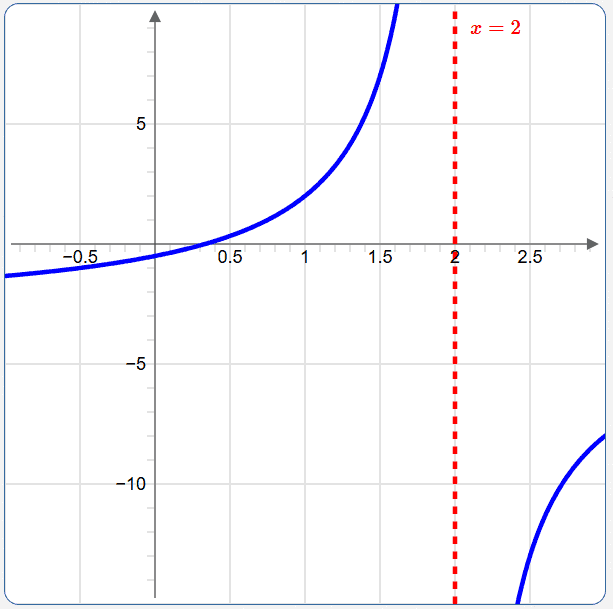
(c) Find the $x$-intercept of the graph.
For this problem, you could use your calculator (and get an estimate) or find the intercept algebraically, which is done here:
- An $x$-intercept is a point with $y$-value equal to $\,0\,.$ So, you need to set $\,\frac{1-3x}{x-2}\,$ equal to $\,0\,.$
- The only way a fraction can equal zero is when its numerator is zero: $$ \begin{gather} 1-3x = 0\cr 1 = 3x\cr x = \frac 13 \approx 0.33333 \end{gather} $$
- The only $x$-intercept is: $$ (\frac 13,0) \approx (0.33333,0) $$ (Note that this agrees with the graph.)
(d) Use your calculator to estimate a value of $\,x\,$ for which $\,f(x) = 5\,$. (Zoom, as necessary, to get $\,f(x)\,$ within $\,0.01\,$ of $\,5\,.$)
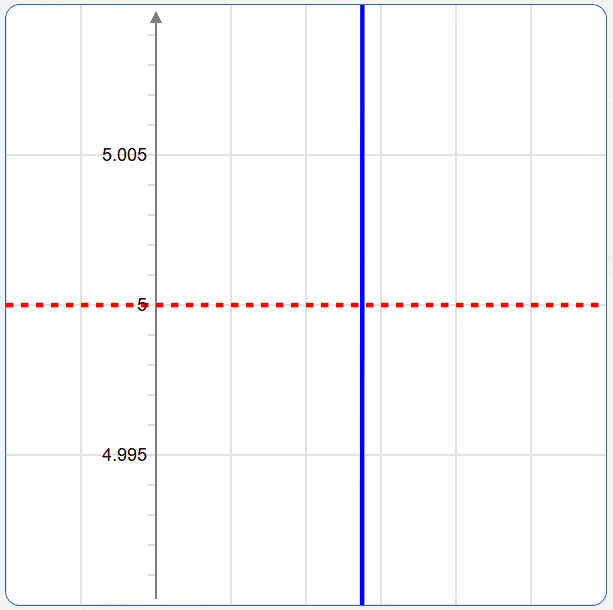
When you zoom in this close, the graph looks nearly vertical! From this graph, it looks like the $x$-value of the intersection of the line $\,y = 5\,$ and $\,y = \frac{1-3x}{x-2}\,$ is a bit less than $\,1.5\,$ (here, $\,x\,$ is still from $\,-1\,$ to $\,3\,.$) Your calculator can get much closer!
Finding it algebraically (which you don't need to do for this problem): $$ \begin{gather} \frac{1-3x}{x-2} = 5\cr\cr 1-3x = 5(x-2)\cr\cr 1-3x = 5x - 10\cr\cr 11 = 8x\cr\cr x = \frac{11}8 = 1.375 \end{gather} $$
Question 6
Write an expression (using the variable $\,x\,$) to represent each sequence of operations.
(a) Take a number, multiply by $\,2\,,$ then subtract $\,3\,.$
$2x - 3$
This expression is written in the most conventional way.
(b) Take a number, subtract $\,3\,,$ then multiply by $\,2\,.$
$2(x-3)$
This expression is written in the most conventional way.
(c) Take a number, multiply it by $\,2\,,$ cube the result, add $\,1\,,$ then divide by the original number.
$\displaystyle\frac{(2x)^3 + 1}x$
This expression is written in a conventional way.
Write the sequence of operations that is being described by each expression.
$3x-1$
Take a number, multiply by $\,3\,,$ then subtract $\,1\,.$
$2(x+1)^3 - 5$
Take a number, add $\,1\,,$ cube the result, multiply by $\,2\,,$ then subtract $\,5\,.$
$\displaystyle\frac{x-3}7 - 1$
Take a number, subtract $\,3\,,$ divide by $\,7\,,$ then subtract $\,1\,.$
Question 7
Let $\,f(x) = x^2 - 2x + 1\,.$ Evaluate each of the following expressions.
(a) $f(0)$
$$ \begin{align} f(0) &= 0^2 - 2\cdot 0 + 1\cr &= 1 \end{align} $$(b) $f(1) - 2$
$$ \begin{align} f(1) - 2 &= (1^2 - 2\cdot 1 + 1) - 2\cr &= 0 - 2\cr &= -2 \end{align} $$(c) $f(f(-1))$
$$ \begin{align} f(f(-1)) &=f\bigl( \overbrace{(-1)^2 - 2(-1) + 1}^{f(-1)}\bigr)\cr &= f(4)\cr &= 4^2 - 2\cdot 4 + 1\cr &= 16 - 8 + 1\cr &= 9 \end{align} $$Notice that we worked from the inside to the outside!
The last two questions assess achievement of the LINEAR FUNCTIONS/EQUATIONS/GRAPHS objectives.
Question 8
Write the equation of the line, in $\,y = mx + b\,$ form, that satisfies the given conditions.
(a) slope $\,3\,,$ passing through the point $\,(2,-1)\,$
This is a perfect candidate for point-slope form, which is then put into $\,y = mx+b\,$ form:
$$ \begin{gather} y - y_1 = m(x - x_1)\cr\cr y - (-1) = 3(x - 2)\cr\cr y + 1 = 3x - 6\cr\cr y = 3x - 7 \end{gather} $$(b) the horizontal line that crosses the $y$-axis at $\,2$
$y = 2$
(c) the line that is perpendicular to $\,x - 3y = 5\,$ and passes through the point $\,(0,3)$
- Find the slope of $\,x-3y = 5\,$: $$ \begin{gather} x - 3y = 5\cr\cr -3y = -x + 5\cr\cr y = \frac x3 - \frac 53 \end{gather} $$ The slope is $\,\frac 13\,.$
- The slope of a perpendicular line is the opposite reciprocal (‘flip’ and take the opposite). This gives $\,-3\,.$
- The line with slope $\,-3\,$ that passes through $\,(0,3)\,$ is: $ y = -3x + 3$
Question 9
A certain telephone company charges a $\,\$4.95\,$ monthly fee, for which the customer gets $\,100\,$ minutes of calls anywhere in the United States. Each additional minute costs $\,7\,$ cents. Carol always talks more than $\,100\,$ minutes. Let $\,x\gt 100\,$ denote the number of minutes that Carol talks in a month, and let $\,C(x)\,$ denote the dollar amount owed to the telephone company. Find a formula for $\,C(x)\,.$
- Fixed charge, with units of dollars: $\,4.95$
- Carol gets $\,100\,$ minutes ‘free’. The number of additional minutes is: $\,x - 100$
- Each additional minute costs $\,7\,$ cents, which is $\,0.07\,$ dollars.
- The dollar cost of the additional minutes is $\,0.07(x - 100)\,.$
- Thus: $\,C(x) = 4.95 + 0.07(x - 100)$
Of course, there are always ‘hidden’ charges (like taxes), but we're ignoring those!