 Solving Simple Linear Inequalities with Integer Coefficients
Solving Simple Linear Inequalities with Integer Coefficients
The only difference between a linear equation in one variable and a linear inequality in one variable is the ‘verb’. Instead of an ‘$\,=\,$’ sign, there is an inequality symbol:
- $\,\lt\,$ (less than)
- $\,\gt\,$ (greater than)
- $\,\le\,$ (less than or equal to)
- $\,\ge\,$ (greater than or equal to)
Only one new idea is needed to solve linear inequalities: if you multiply or divide by a negative number, then the direction of the inequality symbol must be changed. This idea is explored in the current section. We begin with a definition:
Here is a precise statement of the tools for solving linear inequalities. Try translating them yourself, before reading the discussion that follows. Think: “What do these facts tell me that I can do?”
Translating the Theorem
The first sentence,
$a\lt b\ \ \ \text{ is equivalent to }\ \ \ a+c \lt b+c\,,$
says that you can add (or subtract) the same number to (or from) both sides of an inequality, and it won't change the truth of the inequality.
Here's the idea: if $\,a\,$ lies to the left of $\,b\,$ on a number line, and both numbers are translated by the same amount $\,c\,,$ then $\,a+c\,$ still lies to the left of $\,b+c\,.$
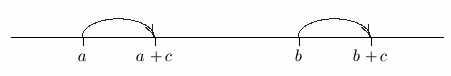
The second sentence,
$a\lt b \ \ \ \text{ is equivalent to }\ \ \ ac \lt bc\,,$
only holds for $\,c \gt 0\,.$ This says that you can multiply (or divide) both sides of an inequality by the same positive number, and it won't change the truth of the inequality.
Here's the idea. Think about the situation when $\,c = 2\,.$ If $\,a\,$ lies to the left of $\,b\,$ on a number line, and we double both number's distance from $\,0\,,$ then $\,2a\,$ still lies to the left of $\,2b\,.$
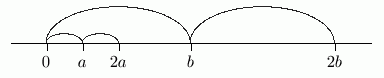
It's the third sentence where something really interesting is happening. The third sentence,
$a\lt b \ \ \ \text{ is equivalent to }\ \ \ ac \gt bc\,,$
holds for $\,c\lt 0\,.$ Notice the ‘$\,\lt\,$’ symbol in the sentence ‘$\,a\lt b\,$’, but the ‘$\,\gt\,$’ symbol in the sentence ‘$\,ac\gt bc\,$’.
This says that if you multiply (or divide) both sides of an inequality by the same negative number, then the direction of the inequality symbol must be changed in order to preserve the truth of the inequality.
Let's look at an example to understand this situation. In the sketch below, ‘$\,a\lt b\,$’ is true, because $\,a\,$ lies to the left of $\,b\,.$ Multiplying both sides by $\,-1\,$ sends $\,a\,$ to its opposite ($\,-a\,$) , and sends $\,b\,$ to its opposite ($\,-b\,$) . Now, the opposite of $\,a\,$ is to the right of the opposite of $\,b\,.$ That is, $\, -a\gt -b\,.$
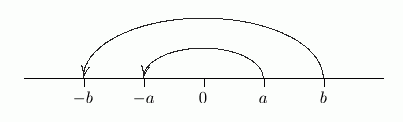
This simple idea is the reason why you must flip the inequality symbol when multiplying or dividing by a negative number.
So remember!
When you multiply or divide both sides of
an inequality by a negative number,
then you must change the direction
of the inequality symbol!
Here are a couple sketches to further help you understand this concept:
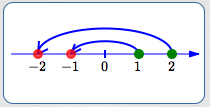
Green for initial inequality.
Red for positions after multiplying by $\,-1\,.$
$1 \lt 2$ $\ldots$
Multiply both sides by $\,-1\,$ to get $\ldots$
$-1 \gt -2$
$1\,$ lies to the left of $\,2\,$ $\ldots$
But $\ldots$
$\,-1\,$ lies to the right of $\,-2$
Put your left hand on $\,1\,.$
Put your right hand on $\,2\,.$
Let both hands follow the arrows.
Your hands cross over!
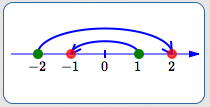
Green for initial inequality.
Red for positions after multiplying by $\,-1\,.$
$1 \gt -2$ $\ldots$
Multiply both sides by $\,-1\,$ to get $\ldots$
$-1 \lt 2$
$1\,$ lies to the right of $\,-2\,$
$\ldots$
But $\ldots$
$\,-1\,$ lies to the left of $\,2$
Put your right hand on $\,1\,.$
Put your left hand on $\,-2\,.$
Let both hands follow the arrows.
Your hands cross over!
Examples
| $-6 - 3x \ge 4$ | original sentence |
| $-3x \ge 10$ | add $\,6\,$ to both sides |
| $x \le -\frac{10}{3}$ | divide both sides by $\,-3\,$; change the direction of the inequality symbol |
Concept Practice
Solve the given inequality. Write the result in the most conventional way.
For more advanced students, a graph is available. For example, the inequality $\,-6 - 3x \ge 4\,$ is optionally accompanied by the graph of $\,y = -6 - 3x\,$ (the left side of the inequality, dashed green) and the graph of $\,y = 4\,$ (the right side of the inequality, solid purple). In this example, you are finding the values of $\,x\,$ where the green graph lies on or above the purple graph.
Click the ‘Show/Hide Graph’ button to toggle the graph.