 Parallel and Perpendicular Lines
Parallel and Perpendicular Lines
Want some other practice with lines?
- Introduction to the Slope of a Line
- Practice with Slope
- Graphing Lines
- Finding Equations of Lines
- Horizontal and Vertical Lines
If you know the slopes of two non-vertical lines, can you easily determine if they're parallel? Perpendicular? Yes!
Parallel lines have the same slope.
Perpendicular lines have slopes that are opposite reciprocals.
This section explores these concepts.
Slopes of Parallel Lines
Two lines in a plane are parallel if they never intersect; they have the same ‘slant’. (For a more rigorous study of parallel lines and related concepts, visit my Geometry course: Parallel Lines.) Slope (or lack of it!) can be used to decide if lines are parallel:
if and only if
(they are both vertical)
or
(they have the same slope)
This statement offers a good opportunity to review the mathematical words ‘if and only if’ and ‘or’. The statement has been visually presented to help you see the mathematical sentence structure more clearly.
- The basic set-up is two distinct lines lying in the same coordinate plane. This condition lurks in the background (is assumed to be true) for all that follows.
-
Two mathematical sentences are
being compared with the words if and only if:
- first sentence: the two lines are parallel
- second sentence: (they are both vertical) or (they have the same slope)
- If and only if is a variation of ‘is equivalent to’. Sentences that are equivalent always have the same truth values—they're true at the same time, and false at the same time. If one is true, so is the other. If one is false, so is the other.
- An ‘or’ sentence is true when at least one of the subsentences is true. The only time an ‘or’ sentence is false is when both subsentences are false.
-
The nice, compact statement above is actually saying a lot. Take a look, if you want, to increase your appreciation of the brevity of the mathematical language:
Slopes of Perpendicular Lines
Now, let's move on to perpendicular lines. Two lines are perpendicular if they intersect at a $\,90^{\circ}$ angle. For example, the $\,x$-axis and $\,y$-axis are perpendicular.
Suppose two non-vertical lines lie in the same coordinate plane. Let $\,m_1\,$ and $\,m_2\,$ denote the slopes of these lines.
The two lines are perpendicular if and only if their slopes are opposite reciprocals: $$\,\cssId{s54}{m_1 = -\frac{1}{m_2}}\,$$
Equivalently, the two lines are perpendicular if and only if their slopes multiply to $\,-1\,$: $$\,\cssId{s59}{m_1m_2 = -1}\,$$
Make sure you understand the opposite reciprocal equation:
$$ \cssId{s61}{m_1 = -\frac{1}{m_2}} $$| one of the slopes | is | the opposite of | the reciprocal of the other slope |
| $\displaystyle \cssId{s63}{m_1}$ | $\displaystyle \cssId{s65}{=}$ | $\displaystyle \cssId{s67}{-}$ | $\displaystyle \cssId{s69}{\frac{1}{m_2}}$ |
For example, what's the reciprocal of $\,2\,$? Answer: $\frac12$
What's the opposite [of the] reciprocal of $\,2\,$? Answer: $-\frac12$
So, the numbers $\,2\,$ and $\,-\frac 12\,$ are opposite reciprocals. Also notice that $\,(2)(-\frac 12) = -1\,.$ So, lines with slopes $\,2\,$ and $\,-\frac12\,$ are perpendicular.
It's easy to see that this is the correct characterization for perpendicular lines, by studying the sketch below:
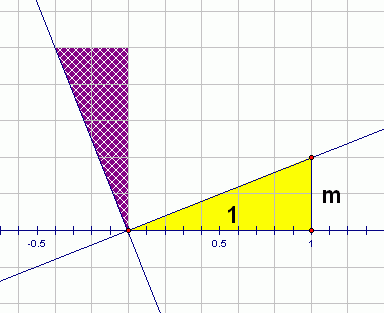
The yellow triangle, with base of length $\,1\,$ and right side of length $\,m\,,$ shows that the slope of the first line is: $$\cssId{s82}{\frac{\text{rise}}{\text{run}}} \cssId{s83}{= \frac{m}1} \cssId{s84}{= m}$$
Now, imagine that this yellow triangle is a block of wood that is glued to the line. Rotate this block of wood counter-clockwise by $\,90^{\circ}\,$ (so that the original base is now vertical).
Using the rotated triangle to compute the slope of the new, rotated, line gives: $$\cssId{s89}{\frac{\text{rise}}{\text{run}}} \cssId{s90}{= \frac{1}{-m}} \cssId{s91}{= -\frac1m}$$ Easy! Voila!