The Test Point Method for Sentences Like:  $f(x) \gt 0$

In Precalculus, it's essential that you can easily and efficiently solve sentences like:

The first sentence is an example of a linear inequality in one variable; a prior lesson covers this type of sentence. For linear inequalities, the variable appears in the simplest possible way—all you have are numbers, times $\,x\,$ to the first power (i.e., terms of the form $\,kx\,,$ where $\,k\,$ is a real number).

The second sentence is an example of a nonlinear inequality in one variable. In nonlinear sentences, the variable appears in a more complicated way—perhaps you have an $\,x^2\,$ (or higher power), or $\,|x|\,,$ or $\,\sin x\,.$ For solving nonlinear inequalities, more advanced tools are needed, which are discussed in detail in this lesson and the next.

There are two basic methods for solving nonlinear inequalities in one variable. These two methods were introduced in the prior lesson, Solving Nonlinear Inequalities in One Variable (Introduction). Both are called ‘test point methods’, because they involve identifying important intervals, and then ‘testing’ a number from each of these intervals.

The two methods are:

• The Test Point Method For Sentences Like ‘$\,f(x) \gt 0\,$’ (this lesson)

  (the One-Function Method; the ‘Compare With Zero’ Method)

• The Test Point Method For Sentences Like ‘$\,f(x) \gt g(x)\,$’ (the next lesson)

  (the Two-Function Method; the ‘Truth’ Method)

There are a few key ideas before we get started:

For example, subtracting $\,3\,$ from both sides of $\,x^2 \ge 3\,$ gives the equivalent inequality $\,x^2 - 3\ge 0\,.$

ONLY TWO PLACES WHERE A FUNCTION CAN CHANGE ITS SIGN: ZEROES and BREAKS

There are only two types of places where the graph of a function $\,f\,$ can go from above to below the $x$-axis (or vice versa):

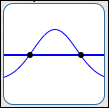
where $\,f(x) = 0$ (at a zero of the function)		SIGN CAN CHANGE AT A ZERO
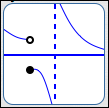
where there's a break in the graph of $\,f$		SIGN CAN CHANGE AT A BREAK

In other words, there are only two types of places where a function can change its sign (from positive to negative, or from negative to positive): at a zero, or at a break.

It's important to note that there doesn't have to be a sign change at a zero, and there doesn't have to be a sign change at a break. These are just the candidates for places where a sign change can occur.

That is, the following implications are true:

• If a function has a sign change at $\,c\,,$ then either $\,f(c) = 0\,$ or there is a break in the graph at $\,c\,.$
• If $\,f(c)\ne 0\,$ and there is no break in the graph of $\,f\,$ at $\,c\,,$ then the function $\,f\,$ does not change its sign at $\,c\,.$

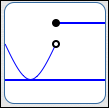
No sign change at this zero; No sign change at this break

The Test Point Method For Sentences Like $\,f(x) \ge 0\,$: Complete Solution With Full Discussion

In this first example, ‘$\,x^2 \ge 3\,$’ is solved using the ‘compare to zero’ (or ‘one-function’) method. A full discussion accompanies this first solution. After, an in-a-nutshell version of the solution is given.

Use the addition property of equality (which also works for inequalities) to rewrite the inequality with zero on the right-hand side:  $\,x^2 - 3\ge 0\,$

Identify the function $\,f\,$ (the function on the left-hand side):

Recall that ‘$\,:=\,$’ means ‘equal, by definition’.  Since the inequality symbol is ‘$\,\ge\,$’, we need to find the values of $\,x\,$ for which the graph of $\,f\,$ lies on or above the $x$-axis.

Identify the candidates for sign changes:

• Places where $\,f(x) = 0\,$:

  $$ \begin{gather} \cssId{s61}{x^2 - 3 = 0}\cr \cssId{s62}{x^2 = 3}\cr \cssId{s63}{x = \pm\sqrt 3} \end{gather} $$
• Breaks in the graph of $\,f\,$:  there are none

Mark the candidates on a number line, using $\,z\,$ (for ‘zero’) as the tick mark. In the diagram below, note the $\,z\,$ at $\,-\sqrt 3\,$ and the $\,z\,$ at $\,\sqrt 3\,.$

(If there were any breaks, they would be marked using ‘$\,B\,$’ as the tick mark.)

The number line itself should be labeled ‘Sign of $\,f(x)\,$’, since you'll be marking the sign (plus or minus) of the function on each subinterval.

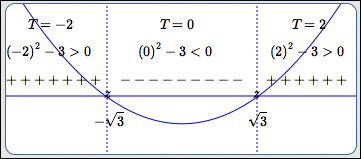Sign of $\,f(x)$

Choose a simple number (the ‘test point’) from each subinterval.

In this example, there are three subintervals:  $(-\infty,-\sqrt 3)\,,$  $(-\sqrt 3,\sqrt 3)\,,$  and  $(\sqrt 3,\infty)\,.$

Since $\,-\sqrt 3\approx -1.7\,,$ the number $-2$ is a good, simple choice from the first subinterval (notice the label ‘$\,T = -2\,$’ above). The function $\,f\,$ is evaluated at $\,-2\,,$ and the result is positive (notice the ‘$\,(-2)^2 - 3 \gt 0\,$’ above). Thus, ‘$\,+\,$’ signs are put on the first subinterval.

Similarly, simple test points are chosen and evaluated for the remaining subintervals. A good rule of thumb—when zero is available as a test point, choose it! Most functions are very easy to evaluate at zero!

Of course, when the graph of the function $\,f\,$ is easy to obtain, it's not necessary to choose test points! The graph of $\,f(x) = x^2 - 3\,$ is shown in the test point sketch above (the holding-water parabola, crossing the $x$-axis at $\,\pm\sqrt 3\,$).

• Where the graph lies above the $x$-axis, the function is positive.
• Where the graph lies below the $x$-axis, the function is negative.
• Where the graph crosses the $x$-axis, the function is zero.

This is much quicker than actually choosing test points!

This test point sketch efficiently displays the sign (plus or minus) of $\,x^2 - 3\,$ everywhere: we know where it is positive (the plus signs), negative (the minus signs), and zero (the ‘$\,z\,$’ tick marks).

So, which values of $\,x\,$ do we want? Since we're solving ‘$\,x^2 - 3 \ge 0\,$’, we need to read off all values of $\,x\,$ corresponding to the plus signs, together with the zeroes.

Using interval notation, the solution set is:

Recall:

• Brackets $\,[\ ,\,]\,$ are used to indicate that an endpoint is included in the solution set.
• The union symbol $\,\cup\,$ (discussed in advanced set concepts) is used to put two sets together.

At first glance, this may seem like a lot of work. Usually, the hardest part is in determining where the function is zero. The web exercise below will give you lots of practice to make you very efficient at the process!

The In-a-Nutshell Version of the Solution

Here is the ‘in-a-nutshell’ version of the previous solution. This is probably the minimum amount of work that a teacher would want you to show.

In the exercises in this section, you will be expected to show all of these steps. The comments are for your information, and do not need to be included in your solutions.

You Write This Down:
$x^2 \ge 3$

Comments:
Original Sentence

$x^2 - 3\ge 0$

Rewrite the inequality with zero on the right-hand side. Since the inequality symbol is ‘$\,\ge\,$’, we need to determine where the graph of $\,x^2 - 3\,$ lies on ($\,=\,$) or above ($\,\gt\,$) the $x$-axis.

$f(x) := x^2 - 3$

If desired, name the function on the left-hand side $\,f\,,$ so it can be easily referred to in later steps. Recall that ‘$:=$’ means ‘equals, by definition’.

$x^2 - 3 = 0$
$x^2 = 3$
$x = \pm\sqrt 3$

(no breaks in graph of $\,f\,$)

Identify the candidates for sign changes for $\,f\,$:

• where $\,f(x)\,$ is zero
• breaks in the graph of $f$

Sign of $\,f(x)\,$

Mark the candidates from the previous step on a number line which is labeled ‘Sign of $\,f(x)\,$’.

Mark zeroes with the tick mark ‘$\,z\,$’.

Test each subinterval to see if $\,f(x)\,$ is $\,+\,$ or $\,-\,.$ Since $\,\sqrt 3\approx 1.7\,,$ test points $\,-2\,$ and $\,2\,$ are easy.

If the graph of $\,f\,$ is easy to obtain, then draw it in. In this case, you don't even need the test points! Graph above the $x$-axis? Then $\,f(x)\,$ is positive. Graph below the $x$-axis? Then $\,f(x)\,$ is negative.

In this test point sketch, both the test points and graph are shown.

Solution set:
$(-\infty,-\sqrt 3\ ] \cup [\ \sqrt 3,\infty)$

Sentence Form of Solution:
$x\le -\sqrt 3\ \ \text{ or }\ \ x\ge \sqrt 3$

Read off the solution set, using correct interval notation. Or, give the sentence form of the solution.

For this problem, since the inequality symbol is ‘$\,\ge\,$’, we need to read off all values corresponding to plus signs and zeroes.

A Second Example: A Function With Both a Break and a Zero

Here is a second example, where there is both a break in the graph and a zero. Only the in-a-nutshell version of the solution is given.

You Write This Down:
$\displaystyle \frac 1x \lt 2$

Comments:
Original Sentence

$\displaystyle \frac 1x - 2 \lt 0$

Rewrite the inequality with zero on the right-hand side.

Since the inequality symbol is ‘$\,\lt\ $’, we need to determine where the graph of $\,\frac 1x - 2\,$ lies below the $x$-axis.

$\displaystyle f(x) := \frac 1x - 2$

If desired, name the function on the left-hand side $\,f\,,$ so it can be easily referred to in later steps. Recall that ‘$:=$’ means ‘equals, by definition’.

When $\,x = 0\,$ there is a break, since division by zero is not allowed. For $\,x\ne 0\,$:

$$ \begin{gather} \cssId{s153}{\frac 1x - 2 = 0}\cr\cr \cssId{s154}{\frac 1x = 2}\cr\cr \cssId{s155}{x = \frac 12} \end{gather} $$

(Take reciprocals of both sides: if two numbers are equal, so are their reciprocals.)

Identify the candidates for sign changes for $\,f\,$:

• where $\,f(x)\,$ is zero
• breaks in the graph of $f$

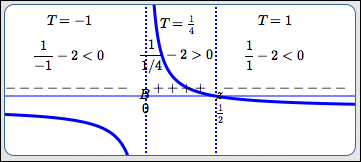Sign of $\,f(x)\,$

Mark the candidates from the previous step on a number line which is labeled ‘Sign of $\,f(x)\,$’.

Mark zeroes with the tick mark ‘$\,z\,$ ’. Mark breaks with the tick mark ‘$\,B\,$ ’.

Test each subinterval to see if $\,f(x)\,$ is $\,+\,$ or $\,-\,.$

If the graph of $\,f\,$ is easy to obtain, then draw it in. In this case, you don't even need the test points! Graph above the $x$-axis? Then $\,f(x)\,$ is positive. Graph below the $x$-axis? Then $\,f(x)\,$ is negative.

In this test point sketch, both the test points and graph are shown.

Solution Set:
$(-\infty,0) \cup (\frac 12,\infty)$

Sentence Form of Solution:
$x \lt 0\ \ \text{ or }\ \ x \gt \frac 12$

Read off the solution set, using correct interval notation. Or, give the sentence form of the solution.

For this problem, since the inequality symbol is ‘$\,\lt\,$’, we need to read off all values corresponding to minus signs.

Using WolframAlpha to Solve Nonlinear Inequalities

Just for fun, jump up to wolframalpha.com and key in the two examples explored in this lesson:

x^2 >= 3
1/x < 2

Voila!