The Addition Property of Equality

In an earlier section, we saw that the sentences ‘$\,2x - 3 = 0\,$’ and ‘$\,x = \frac{3}{2}\,$’ certainly look different,
but are ‘the same’ in a very important way: they always have the same truth.
No matter what number is chosen for $\,x\,$, the sentences are true at the same time, and false at the same time.

Here's the question to be explored in this section and the next:
How do we get from the harder equation $\,2x - 3 = 0\,$ to the simpler equation $\,x = \frac{3}{2}\,$?
That is, what can you do to an equation that will make it look different, but not change its truth?

Two transforming ‘tools’ are needed to change $\,2x - 3 = 0\,$ into $\,x = \frac{3}{2}\,$.
One of these tools (the Addition Property of Equality) is discussed in this section;
the other (the Multiplication Property of Equality) is discussed in the following section.

Here's the way you would be told about one of the most commonly-used transforming tools for equations,
using the language of mathematics:

THEOREM the Addition Property of Equality

For all real numbers

$\,a\,$,

$\,b\,$, and

$\,c\,$:

$$ a = b \ \ \text{⇔}\ \ a + c = b + c $$

Note: Here's how to read aloud that sentence:

$a = b$	$\text{⇔}$	$a + c = b + c$
$a$ equals $b$	is equivalent to	$a+c$ equals $b+c$

To a person not trained in reading mathematics, the information contained in this theorem is completely inaccessible.
If you don't understand the language in which an idea is being expressed, then you can't use the idea.

So, what is this theorem telling us that we can do?

To answer this question, you need to ask yourself:
What did you do to ‘$\,a = b\,$’ to transform it into ‘$\, a + c = b + c\,$’?
ANSWER: You added $\,c\,$ to both sides of the equation.

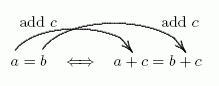
Hence the first part of the translation:

You can add the same number to both sides of an equation,
and this won't change the truth of the equation.

Continuing the translation:
What did you do to ‘$\,a + c = b + c\,$’ to transform it into ‘$\,a = b\,$’?
ANSWER: You subtracted $\,c\,$ from both sides of the equation.

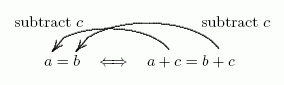
Hence the rest of the translation:

You can subtract the same number from both sides of an equation,
and this won't change the truth of the equation.

So, here's the full translation of the Addition Property of Equality:
this is the way a math teacher might translate the Addition Property of Equality,
to tell students what they can do:

You can add (or subtract) the same number to (or from) both sides of an equation,
and this won't change the truth of the equation.

Here, you will practice recognizing equivalent equations.
Also, you will identify what you are doing to one equation to get an equivalent equation.

EXAMPLES:

Question:
Equation #1:

$x + 2 = 5$
Equation #2:

$x + 3 = 6$
Are these equations equivalent?
If YES, then what did you DO to Equation #1 to get Equation #2?

Solution:
YES; add

$1$ to both sides

Question:
Equation #1:

$x - 1 = 3$
Equation #2:

$3x - 1 = 3 + 2x$
Are these equations equivalent?
If YES, then what did you DO to Equation #2 to get Equation #1?

Solution:
YES; add

$-2x$ to both sides
(or, subtract

$2x$ from both sides)

Question:
Equation #1:

$x + 1 = 3$
Equation #2:

$x = -2$
Are these equations equivalent?
If YES, then what did you DO to Equation #1 to get Equation #2?

Solution:
NOT EQUIVALENT

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
The Multiplication Property of Equality