Solving Linear Inequalities in One Variable

In Precalculus, it's essential that you can easily and efficiently solve sentences like:

$\displaystyle\frac{3x}{2}-1 \ge \frac 15 - 7x$
and
$\displaystyle x^2 \ge 3$

This lesson gives you practice with the first type of sentence, which is a linear inequality in one variable. The next lesson gives you practice with the second type of sentence, which is a nonlinear inequality in one variable.

This page gives an in-a-nutshell review of essential concepts and skills for solving linear inequalities in one variable. If you're needing more, a thorough review is also outlined.

All links to lessons open in a new window, so you don't lose this page.

Solving Linear Inequalities

• It's an inequality because of the ‘$\,\ge\,$’.

  An inequality is a mathematical sentence that uses at least one of the following:

  • $\le$   less than or equal to
  • $\lt$   less than
  • $\ge$   greater than or equal to
  • $\gt$   greater than

• It's an inequality in one variable because it uses only a single variable (in this case, $\,x\,$). That is, it doesn't use (say) both $\,x\,$ and $\,y\,.$

  The single variable can appear any number of times: in the sentence ‘$\displaystyle\,\frac{3\color{blue}{x}}{2}-1 \ge \frac 15 - 7\color{blue}{x}\,$’, it appears twice.

• It's linear since every occurrence of the variable is as simple as possible. For example, there are no $\,x^2\,$ terms, no variables inside trig functions or under square roots, and no variables in denominators.

  All you have are numbers times $\,x\,$ to the first power (i.e., terms of the form $\,kx\,,$ where $\,k\,$ is a real number).

Only extremely basic tools are needed to solve linear inequalities in one variable:

• Similar to the Addition Property of Equality, you can add/subtract the same number to/from both sides of the inequality.

• Similar to the Multiplication Property of Equality, you can multiply/divide both sides of the inequality by a nonzero number.

  However, if you multiply/divide by a negative number, then you must change the direction of the inequality symbol.

  Why is this? Why do you need to flip the inequality when you multiply or divide by a negative number?

Let's look at an example to understand this situation.

In the sketch below, ‘$\,a\lt b\,$’ is true, because $\,a\,$ lies to the left of $\,b\,.$

Multiplying both sides of the inequality by $\,-1\,$ sends $\,a\,$ to its opposite ($\,-a\,$) , and sends $\,b\,$ to its opposite ($\,-b\,$) . Now, the opposite of $\,a\,$ is to the right of the opposite of $\,b\,.$ That is, $\, -a\gt -b\,.$

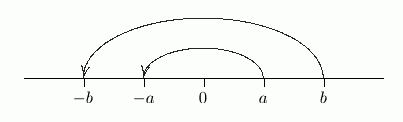
So, multiplying two numbers by $\,-1\,$ changes their left/right positioning relative to each other!

For example, $\,1 \lt 2\,$ (one is to the left of two), but $\,-1 \gt -2\,$ (negative one is to the right of negative two). That's why you need to change the inequality symbol!

Example

So, solution of the sample sentence could look something like this:

By the way, head up to wolframalpha.com and type in:

3x/2 -1 >= 1/5 - 7x

(You can cut-and-paste.) Voila!

For a much more thorough review of solving linear inequalities, do this:

• Start by reading pages 308 and 309 of Solving Linear Equations in One Variable, to make sure you know what the word ‘linear’ means in this context.
• Get some basic practice (no fractions): Solving Simple Linear Inequalities with Integer Coefficients
• Practice with some slightly harder problems (but still no fractions): Solving Linear Inequalities with Integer Coefficients
• Here are linear inequalities involving fractions: Solving Linear Inequalities Involving Fractions
• If desired, here are a bunch of linear inequalities, all mixed up: Solving Linear Inequalities, All Mixed Up

Now, practice solving some fairly complicated linear inequalities by click-click-clicking below. All steps in the solution process are shown.

Each problem is accompanied by an optional graph, which offers additional insights into the solution set. If the information contained in the graph isn't meaningful to you, first study the next section, Solving Nonlinear Inequalities in One Variable (graphical concepts), and then come back!