GRAPH OF THE SECANT FUNCTION

• PRACTICE (online exercises and printable worksheets)

This section discusses the graph of the secant function (shown below).

For ease of reference, some material is repeated from the Trigonometric Functions.

• The secant function: definition and comments
• Where does the graph of the secant function come from?
• Important characteristics of the graph of the secant function

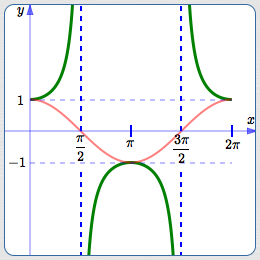
one period of the graph of $\displaystyle y = \sec x := \frac{1}{\cos x}$ (periodic with period $\,2\pi\,$) The cosine curve is shown in red.

Key ideas contributing to the graph: the reciprocal of $\,1\,$ is itself the reciprocal of $\,-1\,$ is itself the number $\,0\,$ has no reciprocal the reciprocal of a small positive number is a large positive number the reciprocal of a small negative number is a large negative number a number smaller than $\,1\,$ has reciprocal bigger than $\,1\,$

The Secant Function: Definition and Comments

• Let $\,t\,$ be a real number (with restrictions noted below).
  Think of $\,t\,$, if desired, as the radian measure of an angle.
• By definition, $\displaystyle \sec t := \frac{1}{\cos t}\,$.
• Using function notation, the number ‘$\,\sec t\,$’ is the output from the secant function when the input is $\,t\,$.
  In other words, ‘$\,\sec\,$’ is the name of the function; $\,t\,$ is the input; $\,\sec t\,$ is the corresponding output.
• Recall the convention: for multi-letter function names, parentheses are usually omitted from function notation.
  That is, $\,\sec(t)\,$ is usually written without parentheses, as $\,\sec t\,$, when there is no confusion about order of operations.
• However, don't ever write something like ‘$\,\sec t + 2\,$’!
  Clarify as either $\,(\sec t) + 2\,$ (better written as $\,2 + \sec t\,$) or $\,\sec(t+2)\,$.
• Pronounce ‘$\,\sec t\,$’ as ‘secant (see-cant) of $\,t\,$’.
• The secant function isn't defined where the cosine is zero; this happens at the terminal points $\,(0,1)\,$ and $\,(0,-1)\,$.
  Thus, secant is not defined for $\displaystyle \,t = \frac{k\pi}{2}\,$ for odd integers $\,k\,$:   $\,k = \ldots, -5, -3, -1, 1, 3, 5,\, \ldots\,$
  Note that the secant function has the same restrictions as the tangent.

Where does the graph of the secant function come from?

The graph of the secant function is easy to obtain as the reciprocal of the cosine function.
The key ideas are illuminated below:

• the red curve is $\,y = \cos x\,$
• the green curve is $\displaystyle\,y = \sec x := \frac{1}{\cos x}\,$

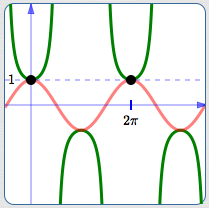
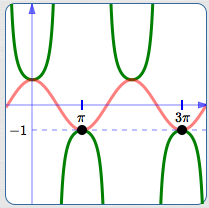
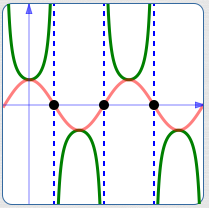
the reciprocal of $\,1\,$ is $\,1\,$, so the points shown do not move	the reciprocal of $\,-1\,$ is $\,-1\,$, so the points shown do not move	zero has no reciprocal: where the cosine is zero, the secant has a vertical asymptote
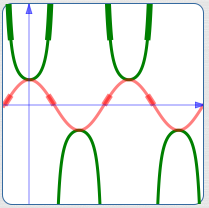
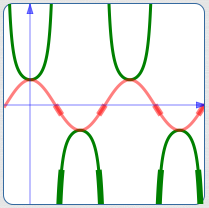
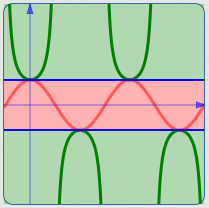
the reciprocal of a small positive number is a large positive number	the reciprocal of a small negative number is a large negative number	the cosine curve is bounded between $\,\color{red}{1}\,$ and $\,\color{red}{-1}\,$; thus, the reciprocals all have size greater than or equal to $\,\color{green}{1}\,$

Important Characteristics of the Graph of the Secant Function

• The period of the secant function is $\,2\pi\,$:
  $\sec(t+2\pi) = \sec t\,$ for all real numbers $\,t\,$ in the domain.
• The domain of the secant function excludes $\,\displaystyle\frac{\pi}{2} + k\pi\,$ for all integers $\,k\,$;
  these are the values where the denominator of the secant function (the cosine) is $\,0\,$.
• The range of the secant function is the set of all real numbers with size greater than or equal to $\,1\,$.
  • Using interval notation:
    $\text{range of secant } = (-\infty,-1] \cup [1,\infty)$
    (Recall from Advanced Set Concepts that ‘$\,\cup\,$’ is the union connective for sets.)
  • Using set-builder notation:
    $\text{range of secant } = \{ x\ \ |\ \ |x| \ge 1\}$
• The secant function has vertical asymptotes every place that it is not defined.
  • Let $\displaystyle\,c = \frac{\pi}{2} + 2\pi k\,$ for integers $\,k\,$. Then:
    • as $\,t \rightarrow c^-\,$, $\,\sec t\rightarrow\infty\,$
    • as $\,t \rightarrow c^+\,$, $\,\sec t\rightarrow -\infty\,$
  • Let $\displaystyle\,c = \frac{3\pi}{2} + 2\pi k\,$ for integers $\,k\,$. Then:
    • as $\,t \rightarrow c^-\,$, $\,\sec t\rightarrow -\infty\,$
    • as $\,t \rightarrow c^+\,$, $\,\sec t\rightarrow \infty\,$