Radian Measure:
Associating Real Numbers with Points on the Unit Circle
Radian Measure:
Associating Real Numbers with Points on the Unit Circle
Up to now, we've been thinking of the trigonometric function inputs as angles with units of degrees. For triangle-based trigonometry (like finding heights of mountains and navigation), this is natural and appropriate.
However, the trigonometric functions are also fundamental in situations where there's not a triangle in sight! In these cases, a different approach is taken.
For example:
- The periodic (repeating) nature of the trigonometric functions makes them valuable when studying repetitive phenomena. For example, Fourier series (important in signal processing) represent periodic signals as sums of sines and cosines.
- Euler's formula (heavily used in mathematics, physics, and engineering) establishes a beautiful relationship between the trigonometric functions and the complex exponential function: $$ \cssId{s10}{{\text{e}}^{ix} = \cos x + i\sin x} $$ Letting $\,x = \pi\,$ (the radian measure for $\,180^\circ\,$) produces what is thought by many to be ‘the most beautiful equation’: $$ \cssId{s12}{{\text{e}}^{i\pi} + 1 = 0} $$ This equation relates five important numbers: the real numbers $\,\text{e}\,,$ $\,\pi\,,$ $\,1\,,$ $\,0\,,$ and the imaginary number $\,i := \sqrt{-1}\,.$
In non-triangle applications, it usually isn't natural to view the trigonometric input as an angle—and there can be disadvantages of doing so. For example, calculus formulas become more complicated when unit-conversion factors are needed to convert degree input to a (unit-free) real number.
When using the trigonometric functions, we often want the input to be a plain 'ole real number—just what we're used to with familiar functions like $\,f(x) = x^2\,.$ Radian measure to the rescue!
You might be thinking—both approaches to trigonometry rely heavily on angles:
- In the right triangle approach, sine and cosine are defined using angles in a right triangle.
- In the unit circle approach, sine and cosine are defined using angles laid out in a standard way in the unit circle.
How can we get angles ‘out of the picture’ and think of the input as just a real number?
The key to success is to establish a relationship between real numbers (points on a real number line) and the unit circle, as follows:
Associating Real Numbers With Points on the Unit Circle
Think of the real number line as an infinite string:

- Black dot at $\,0\,$ (as shown above)
- Positive numbers colored green (extending infinitely to the right)
- Negative numbers colored red (extending infinitely to the left)
Pick up this piece of string and wrap it around the unit circle as follows:
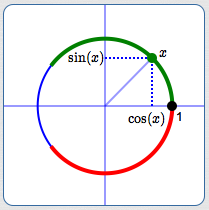
- Put the black dot at the point $(1,0)$ on the unit circle
- Wrap the positive numbers counterclockwise (start up)
- Wrap the negative numbers clockwise (start down)
Of course, the green and red will eventually overlap, as they continue to wrap around and around the circle. (Only a short piece of green and red ‘string’ are shown here!)
In this way, every real number ends up at (is associated with) a unique point on the unit circle—the so-called ‘terminal point’. Then, the usual unit circle definitions apply:
- Cosine is the first coordinate (the $x$-value) of the terminal point
- Sine is the second coordinate (the $y$-value) of the terminal point
As you wrap the real number line ‘string’ around the unit circle, an angle naturally appears (shown below in blue).
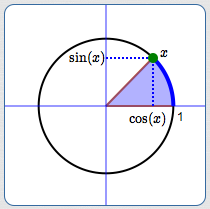
The real number $\,x\,$ is the radian measure of this angle!
So, what is the radian measure of an angle? It's the length of the arc that subtends the angle on the unit circle!
Let $\,\theta\,$ be any angle, laid off in the standard way on the unit circle:
- Start at the positive $x$-axis.
- Positive angles are swept out counterclockwise (start by going up).
- Negative angles are swept out clockwise (start by going down).
The (appropriately-signed) length of the arc subtended by the angle on the unit circle is the radian measure of the angle $\,\theta\,.$
Since the circumference of the unit circle is $\,2\pi r = 2\pi(1) = 2\pi\,,$ half the circumference is $\,\pi\,.$ Thus:
$$\cssId{s53}{\pi \text{ radians} = 180^\circ}$$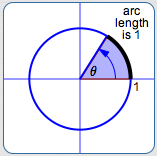
radian measure of $\,\theta\,$ is $\,1\,$
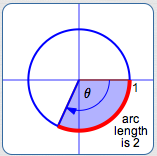
radian measure of $\,\theta\,$ is $\,-2\,$
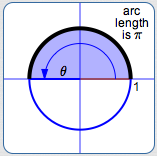
radian measure of $\,\theta\,$ is $\,\pi\,$
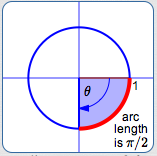
radian measure of $\,\theta\,$ is $\,-\frac{\pi}{2}\,$
Notes on Definition
Numbers given in Radians are just Real numbers. (The fancy typesetting is a memory device!) Remember the association of the real number line with points on the unit circle. Think of the word ‘Radian’ as a gentle Reminder that you're just dealing with a Real number.
The abbreviation for ‘radian’ is ‘rad’. Most people only use the word ‘radian’ or the abbreviation ‘rad’ when there is potential confusion.
For example, $\,\sin(1)\,$ means $\,\sin(1\text{ rad})\,,$ but most people would just say $\,\sin(1)\,.$ If you're in a discussion that also involves $\,\sin(1^\circ)\,,$ then you might want to be kind and say $\,\sin(1 \text{ rad})\,$ for emphasis!
One degree and one radian are very different!
$$ \begin{align} \cssId{s68}{1\text{ radian}}\ &\cssId{s69}{= 1\text{ radian}\cdot\frac{180^\circ}{\pi \text{ radians}}}\cr &\cssId{s70}{\approx 57.3^\circ} \end{align} $$Therefore, the numbers $\sin(1)\,$ and $\,\sin(1^\circ)\,$ are very different, so be careful!
$$\cssId{s72}{\sin(1) = \sin(1\text{ rad}) \approx 0.84}$$ $$\cssId{s73}{\sin(1^\circ) \approx 0.017}$$Converting Between Radian and Degree Measure for Angles
Since $\,\pi\text{ rad} = 180^\circ\,,$ we have:
$$ \cssId{s76}{1 = \frac{180^\circ}{\pi \text{ rad}} = \frac{\pi \text{ rad}}{180^\circ}} $$Conversion between radian and degree measure is then just multiplication by $\,1\,$ in an appropriate form.
From Radians to Degrees
To convert from radians to degrees, multiply by $\,\displaystyle\frac{180^\circ}{\pi}\,$:
$$ \begin{align} \cssId{s80}{x\text { rad}}\ &\cssId{s81}{= x\text { rad}\cdot\frac{180^\circ}{\pi \text{ rad}}}\cr\cr &\cssId{s82}{= \left(\frac{180x}{\pi}\right)^\circ} \end{align} $$From Degrees to Radians
To convert from degrees to radians, multiply by $\,\displaystyle\frac{\pi}{180^\circ}\,$:
$$ \begin{align} \cssId{s85}{x^\circ}\ &\cssId{s86}{= x^\circ\cdot\frac{\pi \text{ rad}}{180^\circ}}\cr\cr &\cssId{s87}{= \frac{\pi x}{180} \text{ rad}} \end{align} $$Common Radian/Degree Measures You Must Know
There are a handful of radian/degree equalities that you should have on your fingertips, because they're so common:
| $180^\circ = \pi \text{ rad}$ | $\displaystyle 90^\circ = \frac{\pi}2 \text{ rad}$ |
| $\displaystyle 45^\circ = \frac{\pi}4 \text{ rad}$ | $360^\circ = 2\pi \text{ rad}$ |
| $\displaystyle 60^\circ = \frac{\pi}3 \text{ rad}$ | $\displaystyle 30^\circ = \frac{\pi}6 \text{ rad}$ |
Why the Name ‘Radian Measure’?
You might think that ‘radian’ is a pretty random name ... ( ... perhaps not any more random than ‘degree’ meaning $\,\frac{1}{360}\,$ of a revolution, or ‘grad’ meaning $\,\frac{1}{400}\,$ of a revolution!)
However, the name ‘radian’ is actually instructive, suggestive, and meaningful, as follows.
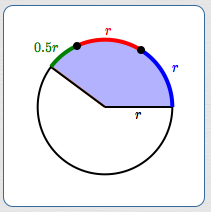
Start with an angle $\,\theta\,$ in a circle of radius $\,r\,.$ Suppose the angle subtends an arc of length $\,s\,,$ as shown below. We want to find the radian measure of $\,\theta\,.$
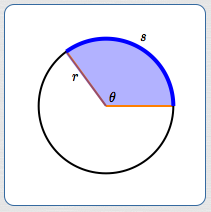
To this end, we must scale the circle to the unit circle. To do this, divide all the lengths through by $\,r\,,$ as shown below.
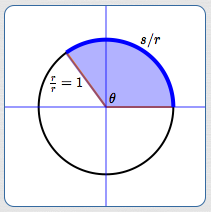
Since the radian measure of an angle is the length of the arc it subtends in the unit circle, we have:
$$ \cssId{s107}{\text{the radian measure of }\theta = \frac{s}{r}} $$Now, think about the interpretation of the division problem $\displaystyle\,\frac{s}{r}\,.$
The division problem $\displaystyle\,\frac{10}{2}\,$ answers the question:
‘How many $2$'s are there in $\,10\,$?’
Answer: $5$
Similarly, the division problem $\displaystyle\,\frac{s}{r}\,$ answers the question:
‘How many $r$'s are there in $\,s\,$?’
Answer: the radian measure of the angle!
The radian measure of an angle gives the number of radiuses needed to subtend the angle!
RADIaN
measure:
the number of
RADiuses
IN
an angle
This knowledge makes it easy to visualize angles that are given in radian measure.
For example, suppose you want to visualize an angle with measure $\,2.5\,$ radians. Draw a circle of any size, as shown below. Imagine cutting a string the length of the radius of the circle. Lay this string around the circle $\,2.5\,$ times:
$$\cssId{s121}{\color{blue}{1r} + \color{red}{1r} + \color{green}{0.5r} = 2.5r}$$Voila! You just laid off an angle with measure $\,2.5\,$ radians!