Introduction to Function Notation
Want some basic practice with functions first? Introduction to Functions
A function is a rule that takes an input, does something to it, and gives a unique corresponding output.
There is a special notation (called ‘function notation’) that is used to represent this situation:
if the function name is $\,f\,,$
and the input name is $\,x\,,$
then the unique corresponding output is called $\,f(x)\,.$
The notation ‘$f(x)\,$’ is read aloud as: ‘ $f$ of $\,x\,$ ’.
So, what exactly is $\,f(x)\,$? Answer: It is the output from the function $\,f\,$ when the input is $\,x\,\,.$
As a second example, what exactly is $\,g(t)\,$? Answer: It is the output from the function $\,g\,$ when the input is $\,t\,.$
Note that $\,f\,$ and $\,f(x)\,$ are different: $f\,$ is the name of the function (the ‘rule’); $f(x)\,$ is the output from this rule when the input is $\,x\,.$
It is often helpful to think of a function as a ‘box’. You drop an input in the top, something happens to the input inside the box, and the output drops out the bottom. The box is labeled with the name of the function.
The letter $\,f\,$ is commonly used as the name of a function, since it is the first letter in the word function.
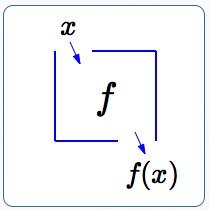A function box:
input: $x$
name of function: $f$
output: $f(x)$
If $\,\,x\,\,$ is dropped in the top of the box labeled $\,f\,,$ then $\,f(x)\,$ comes out the bottom.
If $\,\,t\,\,$ is dropped in the top of the box labeled $\,g\,,$ then $\,g(t)\,$ comes out the bottom.
If $\,x+2t\,$ is dropped in the top of the box labeled $\,h\,,$ then $\,h(x+2t)\,$ (read as ‘ $h$ of $x+2t$ ’) comes out the bottom.
The equation ‘$\,f(x) = x + 2\,$’ is function notation that describes the following situation: a function named $\,f\,$ acts on an input (here, indicated by $\,x\,$), and gives the output $\,f(x)\,,$ which is equal to $\,x+2\,.$ Thus, ‘$\, f(x) = x + 2\,$’ describes the ‘ add $2$ ’ function.
This same function $f$ could also be described by any of these:
$$ \begin{gather} \cssId{s42}{f(t) = t + 2}\cr\cr \cssId{s43}{f(w) = w + 2}\cr\cr \cssId{s44}{f(u) = u + 2} \end{gather} $$The variable used locally to give a name to the input is called a dummy variable.
In the equation $\,f(t) = t + 2\,,$
the dummy variable is $\,t\,.$
In the equation $\,f(w) = w + 2\,,$
the dummy variable is $\,w\,.$
In the equation $\,f(u) = u + 2\,,$
the dummy variable is $\,u\,.$