 Graph of the Tangent Function
Graph of the Tangent Function
This section discusses the graph of the tangent function (shown below). For ease of reference, some material is repeated from the Trigonometric Functions.
- The Tangent Function: Definition and Comments
- Where Does the Graph of the Tangent Function Come From?
- Important Characteristics of the Graph of the Tangent Function
- Tangent as Slope
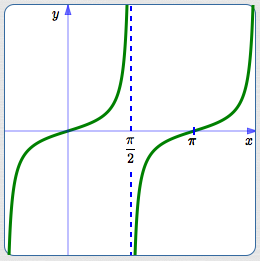
Graph of $y = \tan x$
(periodic with period $\,\pi\,$)
The Tangent Function: Definition and Comments
Let $\,t\,$ be a real number (with restrictions noted below). Think of $\,t\,,$ if desired, as the radian measure of an angle.
By definition: $$\tan t := \frac{\sin t}{\cos t}$$
Using function notation, the number ‘$\,\tan t\,$’ is the output from the tangent function when the input is $\,t\,.$ In other words, ‘$\,\tan\,$’ is the name of the function; $\,t\,$ is the input; $\,\tan t\,$ is the corresponding output.
Recall the convention: for multi-letter function names, parentheses are usually omitted from function notation. That is, $\,\tan(t)\,$ is usually written without parentheses, as $\,\tan t\,\,,$ when there is no confusion about order of operations.
However, don't ever write something like ‘$\,\tan t + 2\,$’ ! Clarify as either $\,(\tan t) + 2\,$ (better written as $\,2 + \tan t\,$) or $\,\tan(t+2)\,.$
Pronounce ‘$\,\tan t\,$’ as ‘tangent of $\,t\,$’.
The tangent function isn't defined where the cosine is zero: this happens at the terminal points $\,(0,1)\,$ and $\,(0,-1)\,.$ Thus, tangent is not defined for $\,t = \frac{k\pi}{2}\,$ for odd integers $\,k\,$: $\,k = \ldots, -5, -3, -1, 1, 3, 5,\, \ldots\,$
Where Does the Graph of the Tangent Function Come From?
Recall that every real number is uniquely defined by its sign (plus or minus) and its size (distance from zero).
Sign of the Tangent Function
The sign of $\,\tan t\,$ is easily determined from its definition as $\,\frac{\sin t}{\cos t}\,$:
- Quadrant I: cosine positive, sine positive, tangent positive
- Quadrant II: cosine negative, sine positive, tangent negative
- Quadrant III: cosine negative, sine negative, tangent positive
- Quadrant IV: cosine positive, sine negative, tangent negative
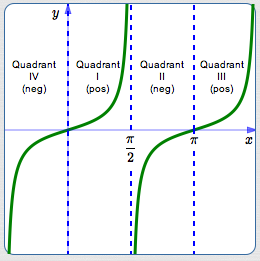
Sign of the Tangent Function
Size of the Tangent Function
The size of the tangent is best understood from its graphical significance in the unit circle approach, as follows:
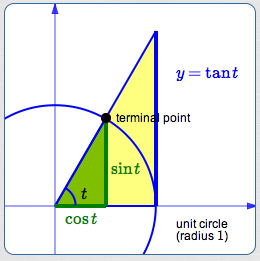
Size of the Tangent Function
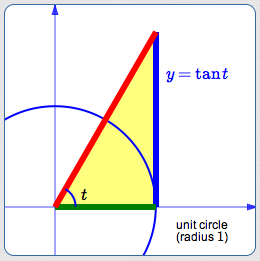
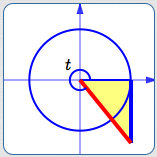
View the real number $\,t\,$ as the radian measure of an angle. Locate the angle $\,t\,$ in the unit circle. The terminal point for $\,t\,$ is shown in black above.
Create an auxiliary (yellow) triangle (it overlaps the green triangle). The base of the yellow triangle has length $\,1\,.$ The right-hand side is perpendicular to the $x$-axis and tangent to the circle.
The green and (overlapping) yellow triangles are similar. Why? They share the same central angle and they both have a right angle.
This chart gives lengths of sides in the green and yellow triangles:
| Bottom of triangle | Right side of triangle | |
| Green triangle: | $\cos t$ | $\sin t$ |
| Yellow triangle: | $1$ |
$y$ (initially unknown) |
By similarity:
$$ \cssId{s52}{\frac{\sin t}{\cos t} = \frac{y}{1}}\,, $$so
$$ \cssId{s54}{\color{blue}{y = \frac{\sin t}{\cos t} := \tan t}} $$Thus, the size of the tangent gives the length of a (particular) segment that is tangent to the unit circle. (The word ‘tangent’ derives from the Latin tangens, meaning ‘touching’.)
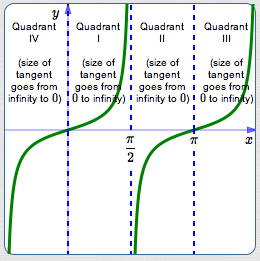
Now, think about what happens to the length of this tangent segment as $\,t\,$ varies:
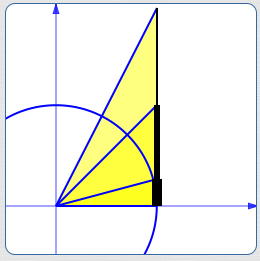
Variations in Length of the Tangent Segment
| As $\,t\,$ goes from | to | the size of $\,\tan t\,$ goes from | to |
| $-\frac{\pi}{2}$ | $0$ | $\infty$ | $0$ |
| $0$ | $\frac{\pi}{2}$ | $0$ | $\infty$ |
| $\frac{\pi}{2}$ | $\pi$ | $\infty$ | $0$ |
| $\pi$ | $\frac{3\pi}{2}$ | $0$ | $\infty$ |
| And so on! | |||
Put the size and sign together to get the graph of the tangent function.

Size of the Tangent Function

Variations in Length of the Tangent Segment
Size of the Tangent Function
Important Characteristics of the Graph of the Tangent Function
The period of the tangent function is $\,\pi\,$: $\,\tan(t+\pi) = \tan t\,$ for all real numbers $\,t\,$ in the domain.
The domain of the tangent function excludes $\,\frac{\pi}{2} + k\pi\,$ for all integers $\,k\,$: these are the values where the denominator of the tangent function (the cosine) is $\,0\,.$
The range of the tangent function is the set of all real numbers: the segment representing the tangent takes on all possible lengths from $\,0\,$ to $\,\infty\,$ (with both positive and negative signs).
The tangent function has vertical asymptotes every place that it is not defined. Let $\,c\,$ denote a real number that is not in the domain of the tangent function. Then:
- as $\,\overbrace{t \rightarrow c^-}^{\text{$t$ approaches $c$ from the left}}\,,$ $\,\tan t\rightarrow\infty\,$
- as $\,\overbrace{t \rightarrow c^+}^{\text{$t$ approaches $c$ from the right}}\,,$ $\,\tan t\rightarrow -\infty\,$
Tangent as Slope
There is an additional insight that comes from studying the diagram below:
The length of the green segment is $\,1\,,$ since it is the radius of the unit circle.
The slope of the red line is therefore:
$$ \cssId{s100}{\frac{\text{rise}}{\text{run}} = \frac{\tan t}{1} = \tan t} $$The tangent gives the slope of the line!
This works in all the quadrants:
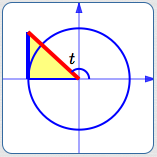
In the second quadrant, $\,\text{slope} = \tan t\,$ is negative
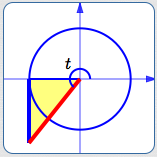
In the third quadrant, $\,\text{slope} = \tan t\,$ is positive
In the fourth quadrant, $\,\text{slope} = \tan t\,$ is negative
Summarizing: Start at the positive $x$-axis and lay off any angle $\,t\,$ (positive, negative, or zero). As long as the angle doesn't yield a vertical line (which has no slope), then $\,\tan t\,$ gives the slope of the resulting line. This is a useful fact in many applications.