 The Period of a Periodic Function
The Period of a Periodic Function
Periodic functions were discussed in the previous lesson. Be sure to read that section first!
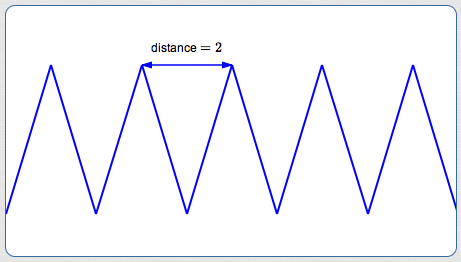
Consider the periodic function $\,f\,$ shown above. Assume that enough of the graph is shown to clearly illustrate the repeating part. (Nothing funny happens outside our viewing window!) That is, the graph continues in this same way forever and ever, both to the right and to the left.
Here are two different questions (and their answers):
-
What is a period of $\,f\,$?
There are infinitely many correct answers to this question: $\,2\,,$ $\,4\,,$ $\,6\,,$ and so on. Any part of the graph of length $\,2\,,$ $\,4\,,$ $\,6\,$ (and so on) can be used as a template to produce the graph.
-
What is the period of $\,f\,$?
There is only one correct answer to this question: $\,2\,.$ The period, by definition, is the least positive period. The period is the length of the shortest template that can be used to produce the graph.
English Lesson: the Articles ‘a’ Versus ‘the’
In English, the articles ‘a’ and ‘the’ are used in different situations.
The article ‘the’ is used to refer to a unique object. When you say ‘the cat’, it is clear that you're referring to one particular cat.
The article ‘a’ allows for more than one object. When you say ‘a cat’, it allows for any cat, not a specific one.
So, you've got to be a bit careful with the language.
If someone stops you on the street, flashes the graph of a periodic function, and asks ‘Hey! What's the period of this function?’ they want the least positive period—the smallest one. They don't want you to list (say) all the multiples of a number. They just want the smallest one that works.
Let's repeat the definition of periodic function from the prior section, this time including the special meaning of the word ‘period’ when it is preceded by the article ‘the’:
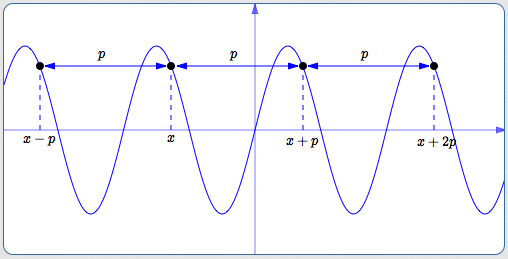
A function $\,f\,$ is periodic if and only if there exists a positive number $\,p\,$ with the following properties:
- Whenever $\,x\,$ is in the domain of $\,f\,,$ so are $\,x\pm p$
- $f(x + p) = f(x - p) = f(x)$
Such a number $\,p\,$ is called a period of the function $\,f\,.$
When a function has a least positive period, then it is given a special name: it is called ‘the period’ of the function.
You might wonder why the definition above didn't simply say:
The least positive period is referred to as ‘the period’ of $\,f\,.$
Here's the problem: there are periodic functions that don't have a least positive period. Don't worry too much—most of the periodic functions you'll deal with do indeed have a least positive period. For a definition, though, we need to be precise.
A Periodic Function with No Least Positive Period
Consider the constant function, $\,f(x) = 7\,.$ No matter what the input is, the output is $\,7\,.$ (Any constant function would work for this example, but $\,7\,$ is the author's favorite number.)
Is $\,f\,$ periodic? The answer is a resounding YES. Indeed, every positive number $\,p\,$ is a period! Why? For every real number $\,x\,,$ and for every $\,p \gt 0\,,$ we have:
$$\cssId{s54}{7 = f(x) = f(x + p) = f(x - p)}$$Every number in the interval $\,(0,\infty)\,$ is a period of $\,f\,.$
Is there a least positive period? In other words, is there a smallest number in the interval $\,(0,\infty)\,$? Nope. The number zero is ‘trying to be’ the least positive period, but unfortunately $\,0\,$ isn't a positive number!
So, if you're asked ‘What is the period of $\,f(x) = 7\,$?’ you'll have to give this answer:
Sorry—constant functions don't have a least positive period.
[Recall that starred material is for more advanced readers, and can be skipped without any loss of continuity.]
There are also non-constant periodic functions with no least positive period.
For example, define a function $\,f\,$ to be $\,1\,$ for rational inputs, and $\,0\,$ for irrational inputs. Then, it can be shown that every positive rational number is a period of $\,f\,.$ So, there is no least positive period.
Hint:
$\text{rational} \pm \text{rational} = \text{rational}$
and
$\text{irrational} \pm \text{rational} = \text{irrational}$
Here's another non-constant periodic function with no least positive period. Its advantage is that it is clear, from construction, that it is indeed periodic.
Define a function $\,f\,,$ as follows:
It has only two outputs, $\,0\,$ and $\,1\,.$
Here's where it equals $\,1\,$:
| At all the integers, as shown at right: |
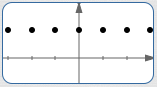
|
| Halfway between all those points: |
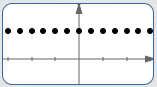
|
| Halfway between all those points: |
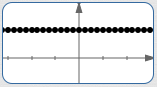
|
Repeat this process ad infinitum (forever and ever). Define $\,f\,$ to equal zero everywhere else.
Clearly, $\,f\,$ is periodic! It's simply a collection of (dense) equally-spaced dots! And, it has arbitrarily small positive periods, hence no least positive period!
The Word ‘Period’ Can Refer to a Number, or a Piece of the Graph
To continue the potential confusion surrounding the word ‘period’, here's yet another use for the word!
Whenever you have a function $\,f\,$ with a least positive period, $\,p\,,$ then the graph of $\,f\,$ on any interval of length $\,p\,$ is often called a period or a cycle of $\,f\,.$
That is, the word ‘period’ (or ‘cycle’) is often used to refer to a smallest possible portion of the graph that could be used as a ‘template’ to produce the entire graph.
For an example, let's return to the graph at the top of the page. Here, the least positive period (i.e., simply ‘the period’) is $\,2\,.$
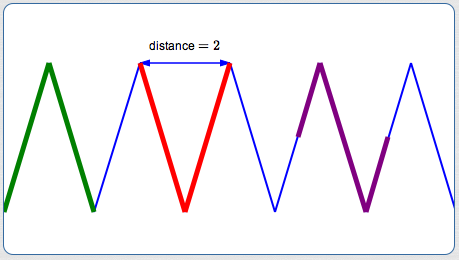
Several periods (cycles) are shown in different colors above (green, red, purple).
Any of these pieces of graph could be used to produce the entire graph! Just begin at its natural starting place, and keep laying it next to itself, over and over again, both to the right and to the left. No shorter piece of graph can accomplish the same thing!
So, the word ‘period’ can refer to a number or to a piece of a graph. How's a person to know which is wanted? Context!!
If your teacher asks ‘What is the period of $\,f\,$?’ then they want a (unique) number.
If your teacher says ‘Please sketch a period of $\,f\,$’ then they want a piece of the graph.