Vectors: From Horizontal/Vertical Components to Direction/Magnitude

Thanks for your support!

 

As shown in an earlier section, the magnitude of $\,\vec v = \langle a\,,\,b\rangle\,$ is: $$ \cssId{s9}{ \|\vec v\| = \sqrt{\strut a^2 + b^2}} $$ In words: the magnitude of a vector is the square root of the sum of the squares of its components.

Magnitude: the Zero Vector

The zero vector is $\,\langle 0\,,\,0\rangle\,.$

• If $\,\vec v = \langle 0\,,\,0\rangle\,,$ then $\,\|\vec v\| = \sqrt{0^2 + 0^2} = 0\,.$
  The zero vector has magnitude zero.
• If $\,\vec v = \langle a\,,\,b\rangle\,$ is a vector with $\,\|\vec v\| = 0\,,$ then $\,\sqrt{a^2 + b^2} = 0\,.$
  The only way this can happen is for both $\,a\,$ and $\,b\,$ to equal zero.
  Thus, $\,\vec v = \langle 0\,,\,0\rangle\,.$
  If a vector has magnitude zero, then it must be the zero vector.
• Putting both directions together:   $\|\vec v\| = 0\,$   if and only if   $\,\vec v = \langle 0\,,\,0\rangle\,$
  

Getting (standard) Direction from Horizontal and Vertical Components

The direction of a vector can be described in different ways. For example, bearings are often used in navigation. The angle conventions used to define the trigonometric functions give a particularly convenient way to define the direction of a vector. For the reader's convenience, this scheme is repeated below: ‘Standard Direction’ Angle Conventions Place the tail of the vector at the origin of a rectangular coordinate system. Indicate the vector's direction using an angle $\,\theta\,$ laid off as follows: start at the positive $x$-axis positive angles are swept out in a counterclockwise direction (start by going up) negative angles are swept out in a clockwise direction (start by going down) When it's necessary to emphasize that this direction scheme is being used, it will be referred to as the standard direction. Standard direction is not unique. For example, $\,\theta = 30^\circ\,$ and $\,\theta = -330^\circ\,$ both describe a vector pointing the same way. In what follows, the symbol $\,\theta\,$ (theta) always refers to standard direction, and simple values of $\,\theta\,$ are used.

standard direction: a positive angle $\,\theta$ 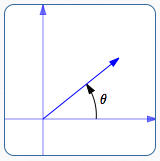standard direction: a negative angle $\,\theta$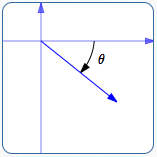

Standard Direction for Vectors pointing Up/Down/Left/Right

When at least one component (horizontal or vertical) of a vector equals zero,
then no formula is needed to find standard direction.
Here's a table that summarizes the results for $\,\vec v = \langle a\,,\, b\rangle\,$:

horizontal/vertical components	arrow representation	standard direction, $\,\theta$
the zero vector: $\,a = 0\,$ and $\,b = 0\,$	(no arrow representation)	the zero vector has no direction; the direction of $\,\langle 0,0\rangle\,$ is undefined
$\,\vec v = \langle a\,,\,0\rangle\,$ with $\,a > 0\,$	vector points to the right	$\,\theta = 0^\circ\,$
$\,\vec v = \langle a\,,\,0\rangle\,$ with $\,a < 0\,$	vector points to the left	$\,\theta = 180^\circ\,$
$\,\vec v = \langle 0\,,\,b\rangle\,$ with $\,b > 0\,$	vector points up	$\,\theta = 90^\circ\,$
$\,\vec v = \langle 0\,,\,b\rangle\,$ with $\,b < 0\,$	vector points down	$\,\theta = 270^\circ\,$ or $\,\theta = -90^\circ\,$

Formula for Standard Direction for Vectors in Quadrants I and IV

For an arbitrary vector, the arctangent function gives convenient formulas for standard direction. However, different formulas are needed in different quadrants. Why are different formulas needed? The arctangent only gives angles between $\,-90^\circ\,$ and $\,90^\circ\,,$ so (without adjustment) it can only cover vectors in quadrants IV and I. Keep reading! Recall that, by definition: $\arctan x\,$ is the angle in the interval $\,(-90^\circ,90^\circ)\,$ whose tangent is $\,x\,$ This is the ‘degree version’ of the definition. Remember: if your calculator is in degree mode, $\,\arctan x\,$ will be in degrees if your calculator is in radian mode, $\,\arctan x\,$ will be in radians For the formulas in this section, $\,\arctan x\,$ is assumed to be in degrees. 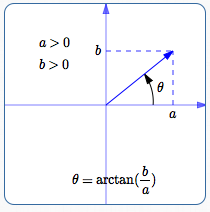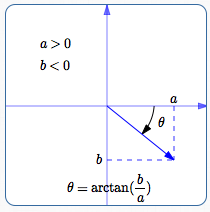In Quadrant I, where $\,a > 0\,$ and $\,b > 0\,,$ everything is simple: $$ \begin{gather} \cssId{s83}{\tan\theta = \frac ba}\cr \cssId{s84}{\theta = \arctan\bigl(\frac ba\bigr)} \end{gather} $$ When $\,\frac ba\,$ is positive, $\,\arctan(\frac ba)\,$ returns the angle between $\,0^\circ\,$ and $\,90^\circ\,$ whose tangent is $\,\frac ba\,.$ This is just the angle we want! Things are similarly easy in quadrant IV. Here, $\,\frac ba\,$ is negative, and $\,\arctan(\frac ba)\,$ returns an angle between $\,-90^\circ\,$ and $\,0^\circ\,.$ Again, this angle provides a correct direction for the vector. If you want a positive angle for the direction (instead of the negative one provided by the arctangent), you can use the formula $\,360^\circ + \arctan(\frac ba) \,.$

The formula for the (standard) direction of a vector $\,\vec v = \langle a\,,\,b\rangle\,$ depends upon the signs of $\,a\,$ and $\,b\,,$ as indicated below: QUADRANT II QUADRANT I QUADRANT III QUADRANT IV

In summary:

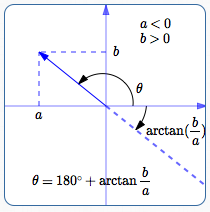
Formula for Standard Direction for Vectors in Quadrants II and III

In Quadrant II, where $\,a < 0\,$ and $\,b > 0\,,$ we have to be careful:

• In Quadrant II, we want a direction angle $\,\theta\,$ between $\,90^\circ\,$ and $\,180^\circ\,.$
• In Quadrant II, $\,\frac ba\,$ is negative, so $\,\arctan(\frac ba)\,$ returns an angle between $\,-90^\circ\,$ and $\,0^\circ\,.$
• In Quadrant II, these are different angles:
  • the (desired, positive) direction angle:   $\,\theta\,$
  • the (undesired, negative) angle:   $\,\arctan(\frac ba)\,$
  Note that both of these angles have tangent value equal to $\,\frac ba\,.$
• To get from $\,\arctan(\frac ba)\,$ to $\,\theta\,,$ just add $\,180^\circ\,$:
  In Quadrant II:   $\,\theta = 180^\circ + \arctan(\frac ba)\,$
  (This formula always yields an angle between $\,90^\circ\,$ and $\,180^\circ\,.$ )

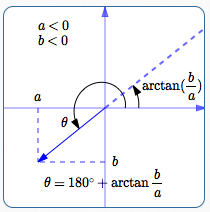
In Quadrant III, where $\,a < 0\,$ and $\,b < 0\,,$ we also have to be careful:

• In Quadrant III, we want a direction angle $\,\theta\,$ between $\,180^\circ\,$ and $\,270^\circ\,.$
• In Quadrant III, $\,\frac ba\,$ is positive, so $\,\arctan(\frac ba)\,$ returns an angle between $\,0^\circ\,$ and $\,90^\circ\,.$
• In Quadrant III, these are different angles:
  • the (desired) direction angle:   $\,\theta\,$
  • the (undesired) angle:   $\,\arctan(\frac ba)\,$
  Note that both of these angles have tangent value equal to $\,\frac ba\,.$
• To get from $\,\arctan(\frac ba)\,$ to $\,\theta\,,$ just add $\,180^\circ\,$:
  In Quadrant III:   $\,\theta = 180^\circ + \arctan(\frac ba)\,$
  (This formula always yields an angle between $\,180^\circ\,$ and $\,270^\circ\,.$ )

The ‘Reference Angle’ Method for finding (standard) Direction

Instead of using the formulas for direction discussed above, you can always find the reference angle for the vector, and then adjust.
The reference angle is the acute angle between the vector and the $x$-axis.

EXAMPLE Find the standard direction of $\,\vec v = \langle -2\,,\,-5\rangle\,.$ Report as a positive angle in the interval $\,[0^\circ,360^\circ)\,.$ Solution: Initially ignore the signs (plus/minus) of the horizontal and vertical components of $\,\vec v = \langle a\,,b\rangle\,.$ Find $\displaystyle\,\arctan\frac{|b|}{|a|}\,.$ This is always a positive, acute angle. Here, $\,\arctan \frac{|-5|}{|-2|} = \arctan\frac 52 \approx 68.2^\circ\,.$ Adjust as needed to get standard direction. In this example, you'll add $\,180^\circ\,$:         standard direction $\,= 68.2^\circ + 180^\circ = 248.2^\circ\,$

You can use WolframAlpha to find the arctangent:

Master the ideas from this section
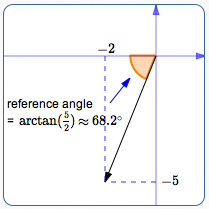
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Vector Application: Finding True Speed and Direction