Introduction to Vectors

This section covers:

• Vectors versus Scalars
• Representation of Vectors
• Size (Magnitude) of a Vector
• Equality of Vectors

Vectors versus Scalars

Scalars

Some quantities can be described by a single number; such quantities are called scalar quantities. Scalar quantities are completely described by their size. Size is also called magnitude.

If you get complete information by asking ‘How much?’ then you're dealing with a scalar quantity. The answer may also include a unit, but there will be a single number.

Area, time, and volume are examples of scalar quantities:

• How much area?  Answer: $\,2\,$ square feet
• How much time?  Answer: $\,3\,$ seconds
• How much volume?  Answer: $\,4\,$ cubic inches

Vectors

A quantity that requires both size and direction to fully describe it is called a vector quantity or—more simply—a vector.

For vector quantities, two questions must be answered to get complete information:

• A question that gives size, like:  How much?  How fast?  How strong?
• A second question:  What direction?

Velocity and force are examples of vector quantities:

• Velocity:  If an object moves, two things are of interest: How fast is it going? (size) In what direction?
• Force:  If you (say) push an object, two things are of interest: How hard are you pushing? (size) In what direction are you pushing?

Representation of Vectors

Graphically, vectors are represented by arrows. Why? Arrows naturally convey size (their length) and direction (the direction they point).

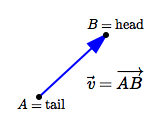
$A\,$ is called the initial point or the tail of the vector.

$B\,$ is called the terminal point or the head of the vector. Memory device:  A creature should lead with its head, not its tail.

For ease of language, most people blur the distinction between a vector and the arrow representing it. Thus, we can say the ‘tail of a vector’ instead of the (more correct) ‘tail of the arrow representing the vector’.

The vector from an initial point $\,A\,$ to a terminal point $\,B\,$ can be notated by $\,\overrightarrow {AB}\,.$   $\overrightarrow{AB}\,$ can be read aloud as ‘vector $\,A\,$ $\,B\,$’.

A single letter can be used to represent a vector. There are several conventional options for notation:

• Put an arrow over the top:  $\,\overrightarrow{v}\,$
• Make the letter bold in a non-italic typeface: $\,\boldsymbol{\rm v}$
• Make the letter bold in an italic typeface: $\,\boldsymbol{v}$

When hand-writing, use $\,\overrightarrow{v}\,,$ since it's difficult to distinguish bold from non-bold in handwriting. Note that the arrow used in the notation for vectors is a reminder that direction is important!

The letter  ‘v’  is commonly used to represent a vector ($\,\overrightarrow{v}\,,$ $\boldsymbol{\rm v}\,,$ $\,\boldsymbol{v}\,$), since it's the first letter in the word vector.

When hand-writing, you often put only a half-arrow over the top, like this: $\,\overset{\rightharpoonup}{\smash{v}\vphantom{b}}\,.$   It's quicker and easier than making the full arrowhead.

When vectors are used together with scalars, it's important to tell them apart. Compare the notations (say) $\,k\,\overrightarrow{v}\,$ with $\,k\,\boldsymbol{\rm v}\,.$ Dr. Burns prefers the notation $\,k\,\overrightarrow{v}\,$ as easiest to tell apart.

Size (Magnitude) of a Vector

The size (magnitude) of a vector is the length of the arrow representing it.

Size is notated by enclosing the vector inside double vertical bars. For example:

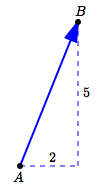
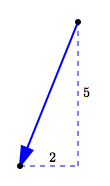
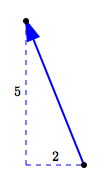
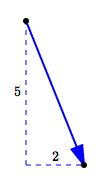
The vectors shown above are all different, because they all have different directions. However, they all have the same size, which is:

The size of a vector is the length of the arrow representing it. In common usage, the words size, magnitude, and length are all used interchangeably in this context. So, these are all the same:

• the size of a vector
• the magnitude of a vector
• the length of a vector

The size of a vector is notated by putting the vector inside double vertical bars. For example:

• the size of vector $\,\overrightarrow{AB}\,$ is notated by $\,\|\overrightarrow{AB}\|$
• the size of vector $\,\overrightarrow{v}\,$ is notated by $\,\|\overrightarrow{v}\|$

Note:

• The size of a real number $\,x\,$ is denoted using absolute value: $\,|x|$
• The size of a vector $\,\overrightarrow{v}\,$ is denoted by $\,\|\overrightarrow{v}\|\,.$
• Some people use  ‘$\,|\cdot|\,$’  for both real numbers and vectors. This is called ‘operator overloading’ in computer science. For beginning math students, it's easiest (and safer) to use different notation.

Since size gives the length of an arrow, it is a nonnegative quantity: 

For all vectors $\,\overrightarrow{v}\,,$ $\,\|\overrightarrow{v}\| \ge 0$

The zero vector is the unique vector of length zero. If a vector has length zero, then it is the zero vector. That is:

$\overrightarrow{v}\,$ is the zero vector

if and only if

$\,\|\overrightarrow{v}\| = 0$

Equality of Vectors

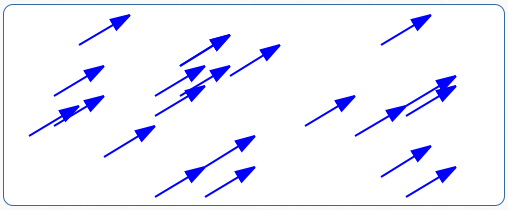
By definition, vectors are equal when they have the same size and the same direction.

All the vectors shown above are equal, since they all have the same size and direction.

In particular, to decide if two vectors are equal, it doesn't matter where they start. All that matters is if they have the same length and the same direction.

The consequence is that vectors are portable. They can be moved to wherever they're needed!