Working With the Arrow Representation for Vectors

Whenever you get a new mathematical object, you need to learn what you can do with it. So ... what operations can be performed with vectors?

• Vectors can be added and subtracted
• Vectors can be multiplied by a scalar (a real number)

In this section, you learn how to perform these operations with the arrow representation for vectors.

In the next section, you learn how to perform these operations with the analytic representation for vectors.

Multiplying a Vector by a Scalar

Let $\,k\,$ be a real number (a scalar). Then, $\,k\overrightarrow{v}\,$ is a vector. That is, a scalar times a vector produces a vector. In other words, a real number times a vector produces a vector.

The image below illustrates the relationship between an original vector $\,\overrightarrow{v}\,$ and various scaled versions:

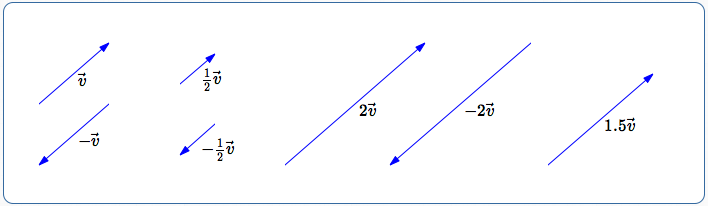
Multiplying a Vector by a Positive Number $\,k$

• Doesn't change the direction of the vector
• Changes the length by a factor of $\,k$

For example:

• If $\,k = 2\,,$ the length is doubled
• If $\,k=\frac 12\,,$ the length is halved

Multiplying a Vector by a Negative Number $\,k$

• Produces a vector pointing in the opposite direction
• Changes the length by a factor of $\,|k|$

For example:

• If $\,k = -2\,,$ the length is doubled, and the vector points in the opposite direction
• If $\,k=-\frac 12\,,$ the length is halved, and the vector points in the opposite direction

Multiplying a Vector by $\,0\,$

Multiplying any vector by the real number $\,0\,$ produces the zero vector.

Multiplying a Vector by $\,-1$

For all vectors $\,\overrightarrow{v}\,,$ $$\cssId{s27}{-\overrightarrow{v}\, := -1\cdot\overrightarrow{v}}$$ is the opposite of $\,\overrightarrow{v}\,.$

Finding the Size of a Scaled Vector

To find the size of a scaled vector, you multiply together two numbers:

• the absolute value (size) of the scaling constant
• the size of the original vector

Precisely, we have:

Keep in mind:

• Whenever you see $\,|\cdot|\,,$ there must be a real number inside. (Note: The centered dot is just a placeholder in this context!)
• Whenever you see $\,\|\cdot\|\,,$ there must be a vector inside.

For example:

So:

A vector and its opposite have the same length.

Adding Vectors (‘Head-to-Tail Addition’)

Adding the arrow representations of vectors is done using the ‘head-of-first to tail-of-second’ rule. This is usually abbreviated as ‘head-to-tail addition’.

Here's how to add $\,\overrightarrow{u}\,$ to $\,\overrightarrow{v}\,$:

• Draw an arrow representing $\,\overrightarrow{u}\,$
• To the head of $\,\overrightarrow{u}\,,$ attach the tail of vector $\,\overrightarrow{v}$
• The sum $\,\overrightarrow{u}+\overrightarrow{v}\,$ goes from the tail of $\,\overrightarrow{u}\,$ to the head of $\,\overrightarrow{v}$

It sounds complicated when written out. The diagram below shows how simple it really is:

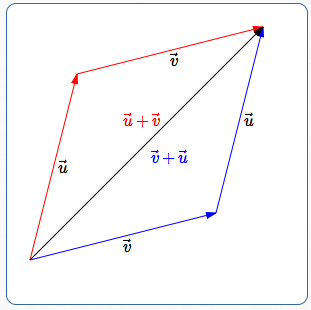
Vector Addition is Commutative

• The configuration to find $\overrightarrow{u} + \overrightarrow{v}\,$ is shown in red:   head of $\,\overrightarrow{u}\,$ is attached to tail of $\,\overrightarrow{v}\,.$
• The configuration to find $\overrightarrow{v} + \overrightarrow{u}\,$ is shown in blue:   head of $\,\overrightarrow{v}\,$ is attached to tail of $\,\overrightarrow{u}\,.$
• In both cases, going from the tail of the first to the head of the second gives the same vector (shown in black).

So, $\,\overrightarrow{u} + \overrightarrow{v} = \overrightarrow{v} + \overrightarrow{u}\,.$ This always works! Vector addition is commutative.

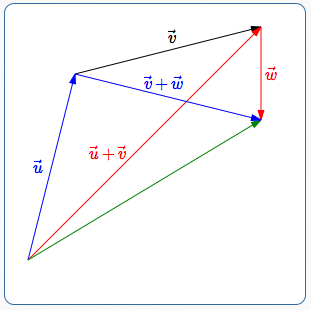
Vector Addition is Associative

• The configuration to find $(\overrightarrow{u} + \overrightarrow{v}) + \overrightarrow{w}\,$ is shown in red:   head of $\,\overrightarrow{u} + \overrightarrow{v}\,$ is attached to tail of $\,\overrightarrow{w}\,.$
• The configuration to find $\overrightarrow{u} + (\overrightarrow{v} + \overrightarrow{w})\,$ is shown in blue:   head of $\,\overrightarrow{u}\,$ is attached to tail of $\,\overrightarrow{v} + \overrightarrow{w}\,.$
• In both cases, going from the tail of the first to the head of the last gives the same vector (shown in green).

So, $\,(\overrightarrow{u} + \overrightarrow{v}) + \overrightarrow{w} = \overrightarrow{u} + (\overrightarrow{v} + \overrightarrow{w})\,.$ This always works! Vector addition is associative.

Therefore, we can write $$\overrightarrow{u} + \overrightarrow{v} + \overrightarrow{w}$$ (no parentheses) without ambiguity.

To add any number of vectors, do head-to-tail addition in any order. The vector from the tail of the first to the head of the last is the vector sum.

Subtracting Vectors

To subtract a vector, just add its opposite:

(Remember that ‘$\,:=\,$’ means ‘equals, by definition’).

Other Operations with Vectors

There are different types of vectors. The vectors we're talking about here are two-dimensional vectors—vectors in a plane.

There are also three-dimensional vectors—vectors in space—and lots more. When you add vectors, they have to be vectors of the same type.

Depending on what type of vectors you're working with, there may be other operations defined. For example, there is a ‘dot product’ and a ‘cross product’ that you'll likely come across if you study Calculus.