Vectors: From Direction/Magnitude to Horizontal/Vertical Components

Let $\,\overrightarrow{v}\,$ be a vector with known magnitude $\,\|\overrightarrow{v}\|\,$ and known direction. How can this information be used to find the analytic form, $\,\overrightarrow{v} = \langle a,b\rangle\,,$ of the vector?

In other words, given the magnitude and direction of a vector, what are its horizontal and vertical components?

Trigonometry gives a simple answer, providing the direction of the vector is specified using the same angle conventions used to define the trigonometric functions. For the reader's convenience, these angle conventions are repeated below:

‘Standard Direction’ Angle Conventions

Place the tail of the vector at the origin of a rectangular coordinate system.

Indicate the vector's direction using an angle $\,\theta\,$ laid off in the standard way:

• Start at the positive $x$-axis
• Positive angles are swept out in a counterclockwise direction (start by going up)
• Negative angles are swept out in a clockwise direction (start by going down)

When it's necessary to emphasize that this direction scheme is being used, it will be referred to as the standard direction.

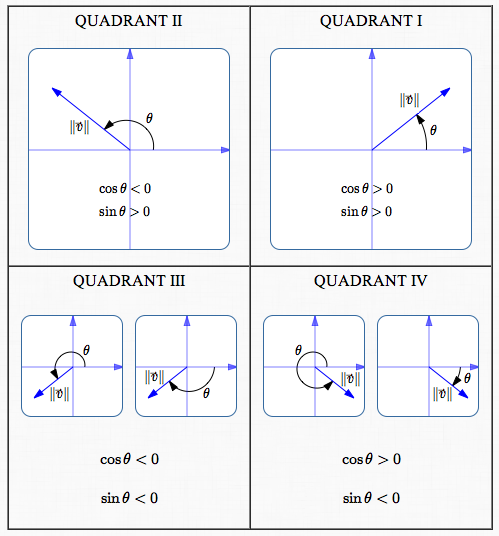
There are infinitely many angles $\,\theta\,$ that ‘end at’ the desired vector. Some possibilities are illustrated above. Any such angle can be used. However, most people cover all possible directions using either:

Nonnegative Angles

• in the interval $\,[0^\circ,360^\circ)\,$  (degree measure)
  
• in the interval $\,[0,2\pi)\,$  (radian measure)

Small Magnitude Angles

• in the interval $\,(-180^\circ,180^\circ]\,$  (degree measure)
• in the interval $\,(-\pi,\pi]\,$  (radian measure)

Given any value of $\,\theta\,$ that works, adding/subtracting any multiple of $\,360^\circ\,$ ($\,2\pi\,$ radians) gives another angle that ends at precisely the same place.

In all these cases: $$\cssId{s29}{\overrightarrow{v} = \langle\, \|\overrightarrow{v}\|\cos\theta \,,\, \|\overrightarrow{v}\|\sin\theta\,\rangle}$$ That is:
The horizontal component is $\,\|\overrightarrow{v}\|\cos\theta$
The vertical component is $\,\|\overrightarrow{v}\|\sin\theta$

Derivation of the Component Formulas: $\,\|\overrightarrow{v}\|\cos\theta\,$ and $\,\|\overrightarrow{v}\|\sin\theta\,$

Start with a point on the unit circle, at the desired angle $\,\theta\,$ for the vector $\,\overrightarrow{v}\,.$

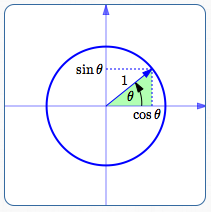
By definition of sine and cosine, the coordinates of the point are $\,(\cos\theta,\sin\theta)\,.$ These are the correct coordinates in all four quadrants.

Multiply all sides of the green triangle by $\,\|\overrightarrow{v}\|\,.$ This gives a new triangle (shown in yellow, below) which has the desired hypotenuse length.

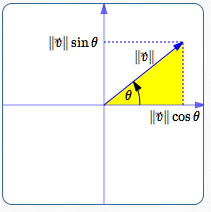
The yellow triangle is similar to the green triangle; all the angles are the same.

What are the coordinates of the head of the vector?

• the $x$-value is $\,\|\overrightarrow{v}\|\cos\theta$
• the $y$-value is $\,\|\overrightarrow{v}\|\sin\theta$

Done! How easy was that?!

Another Way to Specify Direction: Bearings

The direction of a vector can be specified in different ways.

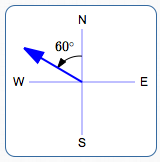
A bearing is an acute angle measured from due north or due south. Bearings are often used for navigation.

For example, the description  ‘ N $\,60^\circ\,$ W ’  means:

• head north
• ‘lean’ $\,60^\circ\,$ towards the west

Here are two memory devices for North-East-South-West:

Never Eat Soggy Waffles

You need to remember to go clockwise from the north. Have trouble remembering the clockwise part? Try this slightly longer version:

As you go through the day, Never Eat Soggy Waffles.

(Time moves forward clockwise!)

WE, not EW!

When west and east are placed correctly, they spell out ‘WE’. If incorrectly placed, they spell out ‘EW’!

A bearing:

N $\,60^\circ\,$ W

A bearing:

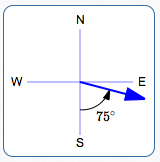
S $\,75^\circ\,$ E

Memory Devices for North/East/South/West:

As you go through the day, Never Eat Soggy Waffles

WE, not EW!

To use the component formulas derived in this section, direction must be specified as an angle from the positive $x$-axis (positive up, negative down).

Two examples of switching from bearings to standard angles $\,\theta\,$ are given below. Of course, infinitely many values of $\,\theta\,$ are possible. Only simple choices are shown here.

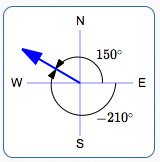
N $\,60^\circ\,$ W

$\theta = 150^\circ$
or
$\theta = -210^\circ\,$

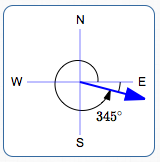
S $\,75^\circ\,$ E

$\theta = -15^\circ$
or
$\theta = 345^\circ$

Example

Find the analytic representation of the vector $\,\overrightarrow{v}\,$ shown below. It has length $\,7\,$ and direction indicated. As needed, round to three decimal places.

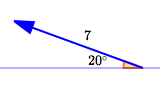
Method I: Use the Component Formulas

• Use:  $\,\theta = 180^\circ - 20^\circ = 160^\circ$
• Horizontal component: $$\cssId{s91}{\|\overrightarrow{v}\|\cos\theta = 7\cos(160^\circ) \approx -6.578}$$
• Vertical component: $$\cssId{s93}{\|\overrightarrow{v}\|\sin\theta = 7\sin(160^\circ) \approx 2.394}$$
• Thus: $\,\overrightarrow{v} = \langle -6.578 , 2.394\rangle$

Method II: Use the Reference Angle; Provide the Correct Signs Yourself

As long as you provide the correct component signs (plus/minus) yourself, then you can use the $\,20^\circ\,$ angle:

• Length of side adjacent to the $\,20^\circ\,$ angle: $$\cssId{s99}{7\cos(20^\circ) \approx 6.758}$$
• Length of side opposite the $\,20^\circ\,$ angle: $$\cssId{s101}{7\sin(20^\circ) \approx 2.394}$$
• The horizontal component is negative; the vertical component is positive.
• Thus: $\,\overrightarrow{v} = \langle -6.578 , 2.394\rangle$