Formula For the Length of a Vector

You may want to review prior sections:

Let $\,\overrightarrow{v} = \langle a,b\rangle\,$ be a vector.

Depending upon the signs (plus or minus) of $\,a\,$ and $\,b\,,$ the vector $\,\overrightarrow{v}\,$ is one of the four vectors shown below. (To match the diagram, suppose that $\,a\,$ and $\,b\,$ are both nonzero.)

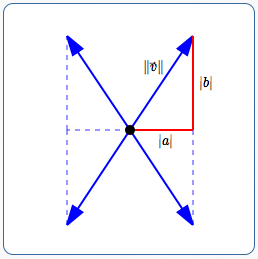
In all four cases, the length (size, magnitude) of $\,\overrightarrow{v}\,$ is the hypotenuse of a triangle with sides of length $\,|a|\,$ and $\,|b|\,.$

Recall that $\,\|\overrightarrow{v}\|\,$ denotes the length of $\,\overrightarrow{v}\,.$ We have:

$$ \begin{align} \cssId{s7}{\|\overrightarrow{v}\|^2} &= \cssId{s8}{|a|^2 + |b|^2}\cr &\qquad \cssId{s9}{\text{(by the Pythagorean Theorem)}}\cr\cr &= \cssId{s10}{a^2 + b^2} \cr &\qquad \cssId{s11}{\substack{\text{($x^2 = |x|^2\,,$ since they have}\\ \text{the same size and sign)}}}\cr \end{align} $$

Take the square root of both sides, and use the fact that $\,\|\overrightarrow{v}\|\ge 0\,.$ The result is the formula for the length of $\,\overrightarrow{v} = \langle a,b\rangle\,$:

$$ \begin{gather} \|\overrightarrow{v}\| = \sqrt{a^2 + b^2}\cr \text{(Vector Length Formula)} \end{gather} $$

$\overrightarrow{v} = \langle a,b\rangle\,$ is one of these four vectors:

$$ \|\overrightarrow{v}\| = \sqrt{a^2 + b^2} $$

Notes on the Vector Length Formula

In Words, to Find the Length of a Vector:

Square the horizontal component
Square the vertical component
Add these squares together
Take the square root of the sum

More compactly:

The length of a vector is the square root of the sum of the squares of the horizontal and vertical components.

If the Horizontal or Vertical Component is Zero

If $\,a\,$ or $\,b\,$ is zero, then you don't need the vector length formula. In this case, the length is just the absolute value of the nonzero component. For example:

$\|\,\langle 5,0\rangle\,\| = 5$
$\|\,\langle 0,-3\rangle\,\| = |-3| = 3$

In general:

$\|\,\langle a,0\rangle\,\| = |a|$
$\|\,\langle 0,b\rangle\,\| = |b|$

However, the vector length formula certainly works—keep reading!

The Correct Formula for Taking the Square Root of a Square

For all real numbers $\,x\,,$ $\sqrt{x^2} = |x|\,.$ Without the absolute value symbol, it doesn't work for negative numbers! For example, $\,\sqrt{(-3)^2} \ne -3\,.$ Be careful!

Using the Vector Length Formula When a Component is Zero

Here's what happens with the vector length formula if one of the components is zero:

$$ \begin{gather} \cssId{s42}{\|\,\langle a,0\rangle\,\|} = \cssId{s43}{\sqrt{a^2 + 0^2}} = \cssId{s44}{\sqrt{a^2}} = \cssId{s45}{|a|}\cr\cr \cssId{s46}{\text{ and }} \cr\cr \cssId{s47}{\|\,\langle 0,b\rangle\,\|} = \cssId{s48}{\sqrt{0^2 + b^2}} = \cssId{s49}{\sqrt{b^2}} = \cssId{s50}{|b|} \end{gather} $$

The formula works, but it's unnecessary in these simple cases.

Finding the Length of a Scaled Vector

Let $\,a\,,$ $\,b\,,$ and $\,k\,$ be real numbers. Let $\,\overrightarrow{v} = \langle a,b\rangle\,.$ Then,

$$ \begin{align} \cssId{s56}{\|k\overrightarrow{v}\|} &\ =\ \cssId{s57}{\|\,k\langle a,b\rangle\,\|}\cr &\qquad \cssId{s58}{\text{(definition of $\,\overrightarrow{v}\,$)}}\cr\cr &\ =\ \cssId{s59}{\|\,\langle ka,kb \rangle\,\|}\cr &\qquad \cssId{s60}{\text{(multiply a vector by a scalar)}}\cr\cr &\ =\ \cssId{s61}{\sqrt{(ka)^2 + (kb)^2}} \cr &\qquad \cssId{s62}{\text{(the vector length formula)}}\cr\cr &\ =\ \cssId{s63}{\sqrt{\strut k^2a^2 + k^2b^2}} \cr &\qquad \cssId{s64}{\text{(exponent law, squaring a product)}}\cr\cr &\ =\ \cssId{s65}{\sqrt{k^2(a^2 + b^2)} } \cr &\qquad \cssId{s66}{\text{(factor)}}\cr\cr &\ =\ \cssId{s67}{\sqrt{\strut k^2}\sqrt{\strut a^2 + b^2}} \cr &\qquad \cssId{s68}{\text{(property of radicals)}}\cr\cr &\ =\ \cssId{s69}{|k| \cdot \sqrt{\strut a^2 + b^2}} \cr &\qquad \cssId{s70}{\text{(since $\ \sqrt{x^2}=|x|\ $)}}\cr\cr &\ =\ \cssId{s71}{|k|\cdot \|\overrightarrow{v}\| }\cr &\qquad \cssId{s72}{\text{(the vector length formula)}} \end{align} $$

So: $$\|k\overrightarrow{v}\| = |k|\cdot \|\overrightarrow{v}\|$$