audio read-through Vector Application: Finding True Speed and Direction

You may want to review prior sections:

Here is a classic problem that uses vectors for its solution:

A plane travels through still air at a given speed, in a specified direction.

A wind (with known speed and direction) blows, pushing the plane off its intended course.

What is the resultant (true) speed and direction of the plane?

Speed

Speed indicates how fast something moves. Speed is a scalar quantity—it is represented by a number (with unit). Here are examples of speed:

Velocity

Velocity is speed together with direction of movement. Velocity is a vector quantity—it has both size (speed) and direction. When solving problems involving velocity, all the tools for working with vectors are available!

Bearings

Bearings are a way to specify direction, often used in navigation. You may want to review bearings before studying the following problem.

A Typical ‘Find True Speed and Direction’ Problem, With Detailed Solution

Problem

A plane flies through wind that blows with a speed of $35$ miles per hour in the direction N $43^\circ$ W .

In still air: the plane has a speed of $550$ miles per hour; the plane is headed in the direction N $60^\circ$ E .

Solution

Identify Speed and Direction For: Plane in Still Air; Wind

Name Speed Direction
Wind ($\,\overrightarrow{W}\,$) $35$ mph N $43^\circ$ W
Plane in still air ($\,\overrightarrow{P}\,$) $550$ mph N $60^\circ$ E

Convert From Bearing to Standard Direction

bearing to standard direction

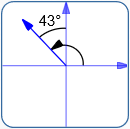
Wind

Bearing:  N $43^\circ$ W

Standard Direction:  $133^\circ$
$\theta_W = 133^\circ$

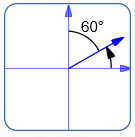
bearing to standard direction

Plane

Bearing:  N $60^\circ$ E

Standard Direction:  $30^\circ$
$\theta_P = 30^\circ$

Convert From Standard Direction and Magnitude to Analytic Form

Recall that if $\,\theta\,$ denotes standard direction, then: $$\overrightarrow{v} = \langle \|\overrightarrow{v}\|\cos\theta\,,\,\|\overrightarrow{v}\|\sin\theta\rangle$$

The length of a velocity vector is speed.  So:

$$\begin{gather} \|\overrightarrow{W}\| = 35 \text{ mph}\cr \text{and}\cr \|\,\overrightarrow{P}\| = 550 \text{ mph} \end{gather} $$

All units are suppressed during computation, for simplicity.

Approximation is fine after getting an exact answer, to better understand the relationship between the vectors (next step). However, be sure to use exact values for future computations.

$$ \begin{align} \cssId{s48}{\overrightarrow{W}}\ &\cssId{s49}{=\ \langle \|\overrightarrow{W}\|\cos\theta_W\,,\,\|\overrightarrow{W}\|\sin\theta_W\rangle}\cr\cr &\cssId{s50}{=\ \langle 35\cos 133^\circ\,,\,35\sin 133^\circ\rangle}\cr\cr &\cssId{s51}{\approx\ \langle -23.9\,,\,25.6\rangle} \end{align} $$
$$ \begin{align} \cssId{s52}{\overrightarrow{P}}\ &\cssId{s53}{=\ \langle \|\overrightarrow{P}\|\cos\theta_P\,,\,\|\overrightarrow{P}\|\sin\theta_P\rangle}\cr\cr &\cssId{s54}{=\ \langle 550\cos 30^\circ\,,\,550\sin 30^\circ\rangle}\cr\cr &\cssId{s55}{=\ \langle \frac{550\sqrt 3}{2}\,,\frac{550}{2}\rangle}\cr\cr &\cssId{s56}{=\ \langle 275\sqrt 3\,,275\rangle}\cr\cr &\cssId{s57}{\approx\ \langle\, 476.3\,,\,275 \, \rangle} \end{align} $$

Note that each component has units of miles per hour. Why?

Make a Rough Sketch of $\,\overrightarrow{P} + \overrightarrow{W}$

A rough sketch of $\,\overrightarrow{P} + \overrightarrow{W}\,,$ using the approximations from the prior step, will reveal how the plane's direction should be ‘adjusted’ due to the wind's influence. This can give you confidence in your final answer, or catch mistakes!

In the rough sketch below, the length of the wind vector is clearly exaggerated. Otherwise, it would be almost invisible compared with the much longer plane vector.

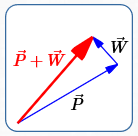
rough sketch: plane vector plus wind vector

Find the True Velocity of the Plane as a Vector

The true velocity of the plane as a vector is $\,\overrightarrow{P} + \overrightarrow{W}\,.$ That is, add the plane and wind vectors. Reinforce good computational habits:  use exact values, and approximate only at the last step.

$$ \begin{align} &\cssId{s69}{\overrightarrow{P} + \overrightarrow{W}}\cr\cr &\quad\cssId{s70}{= \langle 275\sqrt 3\,,275\rangle + \langle 35\cos 133^\circ\,,\,35\sin 133^\circ\rangle}\cr\cr &\quad\cssId{s71}{= \langle 275\sqrt 3 +35\cos 133^\circ\,,\,275 + 35\sin 133^\circ\rangle}\cr\cr &\quad\cssId{s72}{\approx \langle 452.444\,,\,300.597\rangle} \end{align} $$

Find the True Speed of the Plane; Report with Correct Units

The true speed of the plane is the magnitude of the true velocity vector:

$$ \begin{align} &\cssId{s75}{\text{True speed}}\cr\cr &\qquad\cssId{s76}{= \|\text{true velocity}\|}\cr\cr &\qquad\cssId{s77}{= \|\overrightarrow{P} + \overrightarrow{W}\|}\cr\cr &\qquad\cssId{s78}{\approx \sqrt{(452.444)^2 + (300.597)^2}}\cr\cr &\qquad\cssId{s79}{\approx 543.2} \end{align} $$

The true speed of the plane is about $543.2$ miles per hour. In this example, the wind caused the plane to slow down a bit.

Find the True Direction of the Plane

The true direction of the plane is the direction of the true velocity vector.

Review this prior section (as needed) to find the direction of $\,\overrightarrow{P} + \overrightarrow{W}\,.$

First, standard direction is found. In this example, $\,\overrightarrow{P} + \overrightarrow{W}\,$ is in Quadrant I (both components are positive), so:

$$ \begin{align} &\cssId{s87}{\text{True direction}}\cr\cr &\qquad=\cssId{s88}{\ \text{direction of true velocity}}\cr\cr &\qquad\approx\cssId{s89}{\ \arctan \frac{300.597}{452.444}}\cr\cr &\qquad\approx\cssId{s90}{\ 33.6^\circ} \end{align} $$

If requested, this can be reported as a bearing:

$90^\circ - 33.6^\circ = 56.4^\circ$

True direction as a bearing:  N $56.4^\circ$ E

This is in agreement with the adjustment indicated in the rough sketch.

Concept Practice