 Working With the Analytic Representation for Vectors
Working With the Analytic Representation for Vectors
In the previous section, you learned how to use the arrow representation for vectors to perform vector addition and scalar multiplication.
A vector is a mathematical expression. Like all expressions, vectors can have lots of ‘names’—different names are better in different situations.
This section introduces the
analytic representation for vectors,
and shows how vector addition
and scalar multiplication are performed
using this analytic form.
Two Real Numbers, in a Particular Order, Can Convey Different Information
Consider two real numbers ‘$\,a\,,\,b\,$’ (listed in a particular order). This can convey different information, depending upon the context/interpretation:
Location
It can denote a location (position) in a rectangular coordinate system: the intersection of the vertical line $\,x = a\,$ and the horizontal line $\,y = b\,.$ This is the familiar point $\,(a,b)\,.$
Arrow
With the following agreements, it can also denote an arrow:
- the tail of the arrow is $\,(0,0)$
- the head of the arrow is $\,(a,b)$
When using this interpretation, we use the notation $\,\langle a,b\rangle \,.$ In this context, the symbols $\,\langle\,,\,\rangle\,$ are called angle brackets, and $\,\langle a,b\rangle \,$ is the analytic representation of a vector.
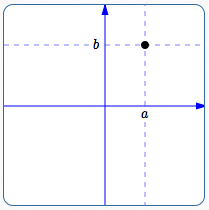
Point $\,(a,b)\,$ specifies a location (position) in a rectangular coordinate system
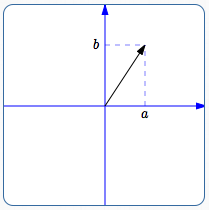
Vector $\,\langle a,b\rangle\,$ specifies an arrow from $\,(0,0)\,$ to $\,(a,b)$
Analytic Representation of a Vector
Let $\,a\,$ and $\,b\,$ be real numbers. The notation
$$\cssId{s25}{\langle a\,,\,b\rangle}$$denotes the unique vector whose arrow representation (positioned at the origin) has tail $\,(0,0)\,$ and head $\,(a,b)\,.$
The notation $\langle a\,,\,b\rangle$ is called the analytic representation of the vector.
- The number $\,a\,$ is called the horizontal component of the vector.
- The number $\,b\,$ is called the vertical component of the vector.
If the arrow representing $\,\langle a\,,\,b\rangle\,$ is positioned at a point other than the origin, then the following thought process is useful:
Start at any point in a plane; this point is the tail of the vector. The horizontal and vertical components give information about how to get from this tail to the head, as follows:
-
Move horizontally a
distance $\,|a|\,$:
- if $\,a \gt 0\,,$ move to the right
- if $\,a \lt 0\,,$ move to the left
-
Move vertically a
distance $\,|b|\,$:
- if $\,b \gt 0\,,$ move up
- if $\,b \lt 0\,,$ move down
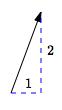
$\langle 1\,,\,2\rangle$
right $1$, up $2$
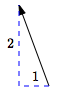
$\langle -1\,,\,2\rangle$
left $1$, up $2$
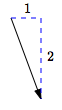
$\langle 1\,,\,-2\rangle$
right $1$, down $2$
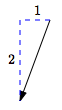
$\langle -1\,,\,-2\rangle$
left $1$, down $2$
Multiplying a Vector in Analytic Form by a Scalar
Let $\,k\,$ be a real number (a scalar). Let $\,\overrightarrow{v} = \langle a,b\rangle\,,$ where $\,a\,$ and $\,b\,$ are any real numbers. Then:
$$ \cssId{s51}{k\overrightarrow{v}} \cssId{s52}{\ =\ k\langle a,b\rangle} \cssId{s53}{\ =\ \langle ka,kb\rangle} $$Notice that both components (horizontal and vertical) get multiplied by the scalar.
Convenient Naming Convention for Vectors in Analytic Form
The horizontal component of a vector $\,\overrightarrow{v}\,$ is commonly named $\,v_1\,$ (and read aloud as ‘vee sub one’).
The vertical component of a vector $\,\overrightarrow{v}\,$ is commonly named $\,v_2\,$ (and read aloud as ‘vee sub two’).
Thus, you often see: $\,\overrightarrow{v} = \langle v_1,v_2\rangle$
If you're conversing with someone while looking at the symbol $\,\langle v_1,v_2\rangle\,,$ then you can read it aloud as simply ‘vee one, vee two’. They'll see the angle brackets and the subscripts, and know that you're talking about a vector.
However, if you're not looking at the symbol $\,\langle v_1,v_2\rangle\,$ (maybe you're talking over the telephone), then for clarity it's better to read it aloud as ‘vector vee sub one, vee sub two’.
Adding/Subtracting Vectors in Analytic Form
Let $\,\overrightarrow{v} = \langle v_1,v_2\rangle\,$ and $\,\overrightarrow{w} = \langle w_1,w_2\rangle\,,$ where $\,v_1\,,$ $\,v_2\,,$ $\,w_1\,,$ and $\,w_2\,$ are real numbers.
Then:
$$ \begin{align} \cssId{s68}{\overrightarrow{v} + \overrightarrow{w}} &\cssId{s69}{\ = \ \langle v_1,v_2\rangle + \langle w_1,w_2\rangle}\cr\cr &\cssId{s70}{\ =\ \langle v_1+w_1\,,v_2+w_2\rangle}\cr\cr\cr \cssId{s71}{\overrightarrow{v} - \overrightarrow{w}} &\cssId{s72}{\ = \ \langle v_1,v_2\rangle - \langle w_1,w_2\rangle}\cr\cr &\cssId{s73}{\ :=\ \langle v_1,v_2\rangle + (-1)\langle w_1,w_2\rangle}\cr\cr &\cssId{s74}{\ =\ \langle v_1,v_2\rangle + \langle -w_1,-w_2\rangle}\cr\cr &\cssId{s75}{\ =\ \langle v_1-w_1,v_2-w_2\rangle} \end{align} $$To add vectors, add their components. To subtract vectors, subtract their components.
As in the previous section, it's important to observe that vector addition is both commutative and associative: