 Unit Vectors
Unit Vectors
You may want to review prior sections:
- Introduction to Vectors
- Working With the Arrow Representation for Vectors
- Working With the Analytic Representation for Vectors
A unit vector is a vector that has length $\,1\,.$
When working with vectors $\,\langle a,b\rangle\,,$ two unit vectors are singled out as being particularly important, and are given special names:
$$ \begin{gather} \cssId{s4}{\hat{\imath} = \langle 1,0\rangle}\cr\cr \cssId{s5}{\hat{\jmath} = \langle 0,1\rangle} \end{gather} $$How to Read Aloud
- Read $\,\hat{\imath}\,$ aloud as ‘ i hat ’.
- Read $\,\hat{\jmath}\,$ aloud as ‘ j hat ’.
Drop the Dots
When you put a ‘hat’ on ‘ i ’ or ‘ j ’, you drop the dot:
- Write $\,\hat{\imath}\,,$ not $\,\hat{i}$
- Write $\,\hat{\jmath}\,,$ not $\,\hat{j}$
Another Name for Vectors: Unit Vector Form
Every vector $\,\langle a,b\rangle\,$ can be easily expressed in terms of $\,\hat{\imath}\,$ and $\,\hat{\jmath}\,,$ as follows:
$$ \begin{align} \cssId{s17}{\langle a,b\rangle} \ &\cssId{s18}{= \ \langle a,0\rangle + \langle 0,b\rangle}\cr\cr &\cssId{s19}{= \ a\langle 1,0\rangle + b\langle 0,1\rangle}\cr\cr &\cssId{s20}{= \ a\hat{\imath} + b\hat{\jmath}} \end{align} $$The name ‘$\,a\hat{\imath} + b\hat{\jmath}\,$’ is called the unit vector form of the vector $\,\langle a,b\rangle\,.$
There are Infinitely Many Unit Vectors
However, $\,\hat{\imath}\,$ and $\,\hat{\jmath}\,$ are simplest.
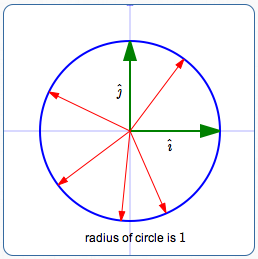
Any vector from the center to a point on this circle has length $\,1\,,$ and hence is a unit vector.
Adding Vectors in Unit Vector Form
$$ \begin{align} &\cssId{s26}{ \color{red}{(a\hat{\imath} + b\hat{\jmath}) + (c\hat{\imath} + d\hat{\jmath})}}\cr\cr &\qquad\cssId{s27}{= \langle a,b\rangle + \langle c,d\rangle}\cr\cr &\qquad\cssId{s28}{= \langle a+c\,,\,b+d\rangle}\cr\cr &\qquad\cssId{s29}{= \color{red}{(a+c)\hat{\imath} + (b+d)\hat{\jmath}}} \end{align} $$Multiplying Vectors in Unit Vector Form by a Constant
$$ \begin{align} &\cssId{s31}{\color{red}{k(a\hat{\imath} + b\hat{\jmath})}}\cr\cr &\qquad\cssId{s32}{= k\langle a,b\rangle}\cr\cr &\qquad\cssId{s33}{= \langle ka\,,\,kb\rangle}\cr\cr &\qquad\cssId{s34}{= \color{red}{ka\hat{\imath} + kb\hat{\jmath}}} \end{align} $$The idea is as simple as ‘combining like terms’! Just gather together the $\,\hat{\imath}\,$ and $\,\hat{\jmath}\,$ terms separately.
You don't always have $\,\hat{\imath}\,$ first and $\,\hat{\jmath}\,$ second, so be careful. They're often all mixed up. Here's an example:
$$ \begin{align} &\cssId{s40}{3\hat{\jmath} + 7\hat{\imath} - 5(2\hat{\imath} - \hat{\jmath})}\cr\cr &\qquad\cssId{s41}{=\quad 3\hat{\jmath} + 7\hat{\imath} - 10\hat{\imath} + 5\hat{\jmath}}\cr\cr &\qquad\cssId{s42}{=\quad -3\hat{\imath} + 8\hat{\jmath}} \end{align} $$