 Vector Application: Forces Acting on an Object in Equilibrium
Vector Application: Forces Acting on an Object in Equilibrium
You may want to review some prior sections:
- Introduction To Vectors
- Working With the Arrow Representation for Vectors
- Working With the Analytic Representation for Vectors
- Unit Vectors
- Formula For the Length of a Vector
- Vectors: From Direction/
Magnitude to Horizontal/ Vertical Components - Vectors: From Horizontal/
Vertical Components to Direction/ Magnitude
Forces are vectors. Why? Forces have both size and direction. For example, if you're pushing an object:
- The size of the force is how hard you're pushing
- The direction of the force is the direction that you're pushing
Depending on the definition being used, the weight of an object can be considered as either a vector or a scalar:
- Weight as a vector: weight is the force of gravity acting on an object
- Weight as a scalar: weight is the size of the force of gravity acting on an object
In the United States, a common unit of weight is the pound, abbreviated as ‘lb’.
Free-Body Diagram
A free-body diagram shows all the forces acting on an object. A typical free-body diagram is shown below.
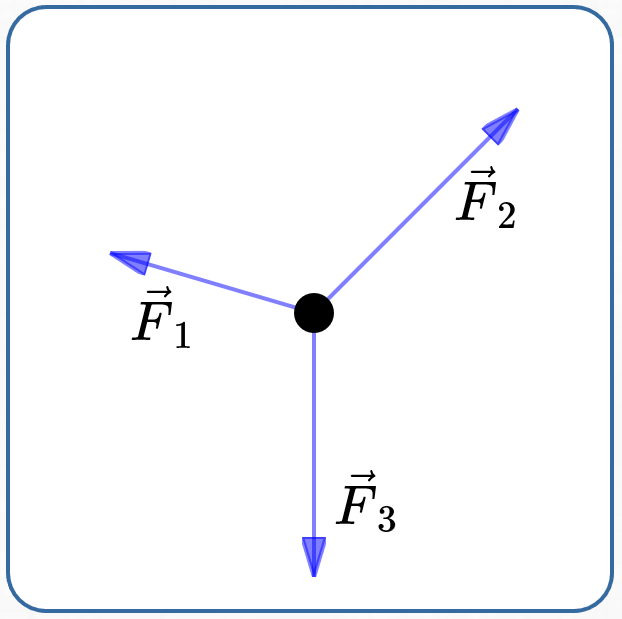
An Object In Equilibrium
By definition, an object is in equilibrium if the sum of the forces acting on the object is the zero vector. The zero vector is denoted by: $\,\overrightarrow{0}$
If an object is at rest (not moving), then it is in equilibrium.
Note about the other direction: If an object is in equilibrium, then its velocity is not changing—it is either at rest, or moving at a constant velocity.
Simpler Notation for the Length of a Vector
The notation $\,\|\overrightarrow{F}\|\,$ for the length of a vector $\,\overrightarrow{F}\,$ can get tedious. Sometimes, a simpler notation is used: Let $\,F\,$ (without an arrow) denote the length of $\,\overrightarrow{F}\,.$ This simpler notation will be used in this section.

A typical free-body diagram
Example: Finding Tensions in Cables
Problem
Two cables are supporting a $200$ pound object, as shown below. Find the tensions in the cables (as vectors).
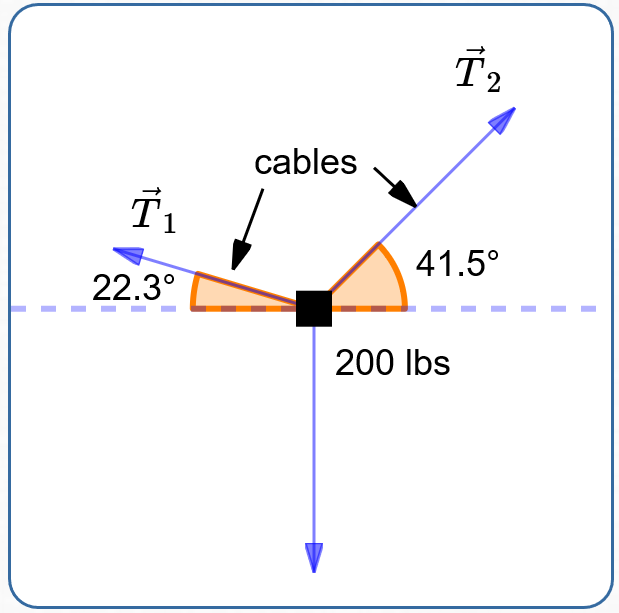
Solution
Let $\,\overrightarrow{T_1}\,$ and $\,\overrightarrow{T_2}\,$ denote the cable tensions, as shown. Let $\,T_1\,$ and $\,T_2\,$ denote the lengths of $\,\overrightarrow{T_1}\,$ and $\,\overrightarrow{T_2}\,,$ respectively. The suspended object causes a $200$ lb force pointing straight down.
Since the object is at rest (assume the cables don't break), it is in equilibrium. There are different ways to write down the equilibrium condition and then solve for the desired tensions.
Take a look at the variations shown below, and decide which you like best! The author (Dr. Burns) prefers Approach #1.
The methods shown below will use some/all of the following information:
- Size is a nonnegative quantity. That is, size (length) is always greater than or equal to zero.
- Since $\,T_1\,$ and $\,T_2\,$ (no arrows) are lengths, they are nonnegative.
- For acute angles $\,\theta\,,$ $\,\cos\theta\,$ and $\,\sin\theta\,$ are both positive.
Sizes of Components

| Vector | Size of Horizontal Component | Size of Vertical Component |
| $\,\overrightarrow{T_1}\,$ | $T_1\cos 22.3^\circ$ | $T_1\sin 22.3^\circ$ |
| $\,\overrightarrow{T_2}\,$ | $T_2\cos 41.5^\circ$ | $T_2\sin 41.5^\circ$ |
| Weight Vector | $0$ | $200$ |

Signs (Plus/Minus) of Components
| Vector | Sign of Horizontal Component | Sign of Vertical Component |
| $\,\overrightarrow{T_1}\,$ | negative (points to the left) | positive (points up) |
| $\,\overrightarrow{T_2}\,$ | positive (points to the right) | positive (points up) |
| Weight Vector | ($0$ has no sign) | negative (points down) |
Reference Angle Analytic Forms of Tension Vectors

Recall that the reference angle is the smallest angle between the vector and the $x$-axis. Just put together the sizes and signs of the components:
$$ \begin{gather} \cssId{s74}{\overrightarrow{T_1} = \langle -T_1\cos 22.3^\circ\,,\,T_1\sin 22.3^\circ \rangle}\cr\cr \cssId{s75}{\overrightarrow{T_2} = \langle T_2\cos 41.5^\circ\,,\,T_2\sin 41.5^\circ \rangle} \end{gather} $$Standard Direction Analytic Forms of Tension Vectors

Standard direction for $\,\overrightarrow{T_1}\,$ is: $$180^\circ - 22.3^\circ = 157.7^\circ$$
$$ \begin{gather} \cssId{s78}{\overrightarrow{T_1} = \langle T_1\cos 157.7^\circ\,,\,T_1\sin 157.7^\circ \rangle}\cr\cr \cssId{s79}{\overrightarrow{T_2} = \langle T_2\cos 41.5^\circ\,,\,T_2\sin 41.5^\circ \rangle} \end{gather} $$Analytic Form of Weight Vector
$$ \cssId{s81}{\text{Weight Vector} = \langle 0,-200\rangle} $$Slightly Different Approaches to Satisfy the Equilibrium Condition
Approach #1 is shortest, and is preferred by Dr. Burns.
Approach #1
The size of the components pointing left must equal the size of the components pointing right:
$$ \cssId{s86}{T_1\cos 22.3^\circ = T_2\cos 41.5^\circ} $$The sum of the sizes of the components pointing up must equal the size of the component pointing down:
$$ \cssId{s88}{T_1\sin 22.3^\circ + T_2\sin 41.5^\circ = 200} $$System of Equations to be Solved
$$\begin{gather} \cssId{s90}{T_1\cos 22.3^\circ = T_2\cos 41.5^\circ}\cr\cr \cssId{s91}{T_1\sin 22.3^\circ + T_2\sin 41.5^\circ = 200} \end{gather} $$Approaches #2 and #3 both use the same idea: For an object in equilibrium, the sum of the forces is the zero vector. The only difference is the naming of the forces:
- Approach #2 uses the reference angle analytic form.
- Approach #3 uses the standard direction analytic form.
Approach #2
Sum the reference angle versions of the forces, and set equal to the zero vector:
$$ \cssId{s99}{\overrightarrow{T_1} + \overrightarrow{T_2} + \text{Weight Vector} = \overrightarrow{0}} $$For two vectors to be equal, their components must be equal.
System of Equations to be Solved
$$ \begin{gather} \cssId{s104}{\color{red}{-T_1\cos 22.3^\circ + T_2\cos 41.5^\circ} = \color{red}{0}}\cr\cr \cssId{s105}{\color{green}{T_1\sin 22.3^\circ + T_2\sin 41.5^\circ -200} = \color{green}{0}} \end{gather} $$Approach #3
Sum the standard direction versions of the forces, and set equal to the zero vector:
$$ \cssId{s108}{\overrightarrow{T_1} + \overrightarrow{T_2} + \text{Weight Vector} = \overrightarrow{0}} $$For two vectors to be equal, their components must be equal.
System of Equations to be Solved
$$ \begin{gather} \cssId{s113}{T_1\cos 157.7^\circ + T_2\cos 41.5^\circ = 0}\cr\cr \cssId{s114}{T_1\sin 157.7^\circ + T_2\sin 41.5^\circ -200 = 0} \end{gather} $$Solve the Resulting System of Equations in $\,T_1\,$ and $\,T_2$
Since $\,\cos 157.7^\circ = -\cos 22.3^\circ\,,$ a moment's inspection shows that the three systems of equations are equivalent.
Use your favorite technique (perhaps substitution or elimination) to solve the system of your choice.
For your convenience, the system in Approach #1 is solved here:
From the first equation:
$$ \cssId{s123}{T_1 = T_2\,\frac{\cos 41.5^\circ}{\cos 22.3^\circ}} $$Substituting into the second equation:
$$ \cssId{s125}{T_2\,\frac{\cos 41.5^\circ}{\cos 22.3^\circ}(\sin 22.3^\circ) + T_2\sin 41.5^\circ = 200} $$Solving for $\,T_2\,$:
Solving for $\,T_1\,$:
$$ \cssId{s129}{T_1 = T_2\frac{\cos 41.5^\circ}{\cos 22.3^\circ} \approx 166.943} $$It is most reliable to zip up to WolframAlpha and type in:
x*cos(22.3 deg) = y*cos(41.5 deg),
x*sin(22.3 deg) + y*sin(41.5 deg) = 200
Here's a screen shot of the input and result from WolframAlpha:
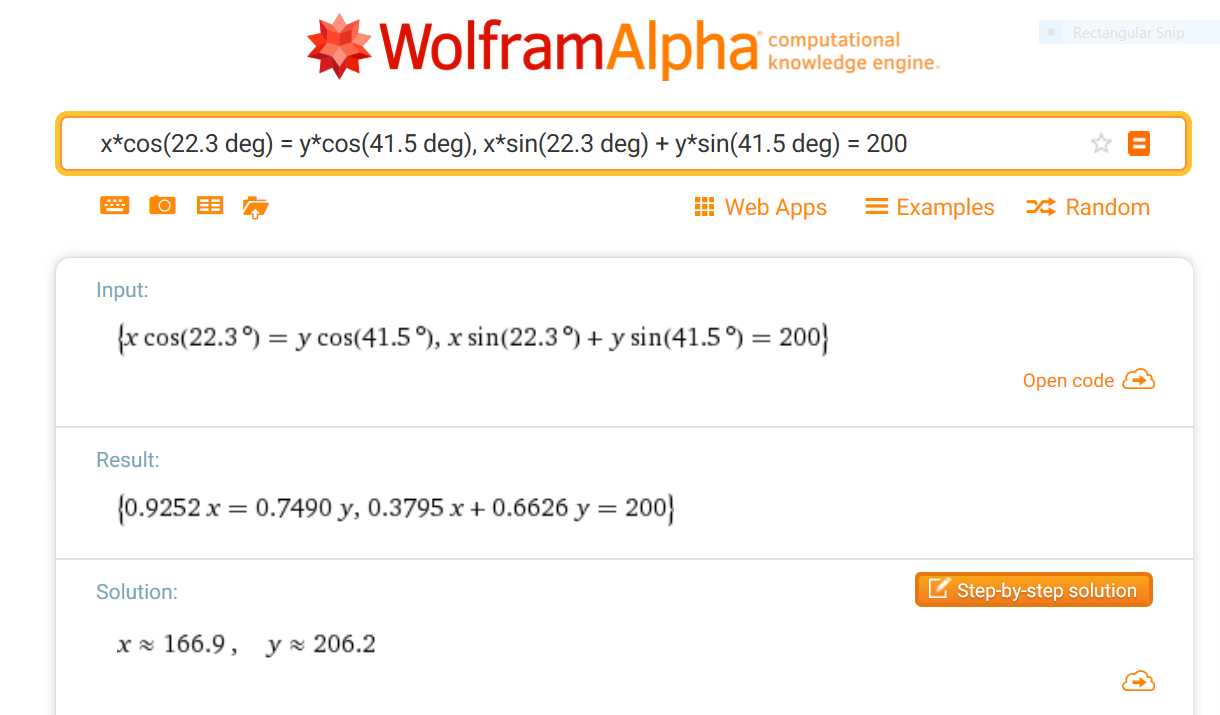
Find the Tensions in the Cables (As Vectors)
These two observations should provide confidence in your answer:
- The horizontal components cancel out: $$-154.457 + 154.457 = 0$$
- The sum of the vertical components is the weight: $$63.348 + 136.652 = 200$$