audio read-through The Distance Formula

Want practice with preliminary concepts first?

The Distance Formula
The distance between points $\,(x_1,y_1)\,$ and $\,(x_2,y_2)\,$ is given by the Distance Formula: $$ \cssId{s7}{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}} $$

Here, $\,x_1\,$ (read as ‘$\,x\,$ sub $\,1\,$’) denotes the $\,x$-value of the first point, and $\,y_1\,$ (read as ‘$\,y\,$ sub $\,1\,$’) denotes the $\,y$-value of the first point. Similarly, $\,x_2\,$ and $\,y_2\,$ denote the $\,x$-value and $\,y$-value of the second point.

This formula involves differences (subtraction problems) that are squared. Notice that $\,(a-b)^2\,$ is equal to $\,(b-a)^2\,.$ Why? Firstly, $\,a-b\,$ and $\,b-a\,$ are opposites, since $\,a - b = (-1)(b - a)\,.$ Secondly, when you square a number and its opposite, you get the same result.

Alternatively, you could FOIL both out and observe that they're the same:

$$ \begin{align} \cssId{s21}{(a-b)^2}\ &\cssId{s22}{= (a-b)(a-b)}\cr &\cssId{s23}{= a^2 - ab - ab + b^2}\cr &\cssId{s24}{= a^2 - 2ab + b^2}\cr\cr \cssId{s25}{(b-a)^2}\ &\cssId{s26}{= (b-a)(b-a)}\cr &\cssId{s27}{= b^2 - ab - ab + a^2}\cr &\cssId{s28}{= a^2 - 2ab + b^2} \end{align} $$

Thus, in the Distance Formula, you can do the subtractions in any order you want, and it won't affect your result. Also, because of the Commutative Property of Addition, you can work with the $\,x\,$ or $\,y\,$ values first—your choice. That is, $$ \begin{align} &\cssId{s33}{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}}\cr &\quad \cssId{s34}{= \sqrt{(y_2-y_1)^2 + (x_2-x_1)^2}} \end{align} $$

In words, to find the distance between two points, do the following:

The Distance Formula follows easily from the Pythagorean Theorem, as suggested by the picture below:

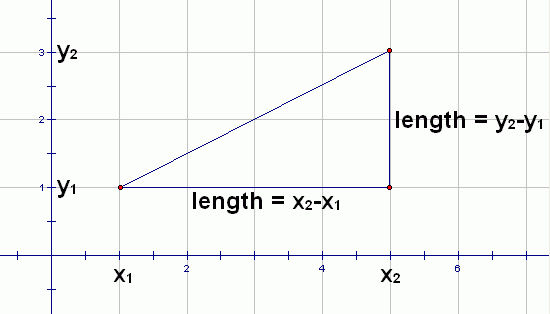
the Distance Formula follows from the Pythagorean Theorem

By the Pythagorean Theorem, $$ \cssId{s42}{{\text{hypotenuse}}^2} \cssId{s43}{= (x_2-x_1)^2 + (y_2-y_1)^2} $$ Solve for the hypotenuse!

Examples

Question: Find the distance between $\,(1,-3)\,$ and $\,(-2,5)\,.$
Solution: $$ \begin{align} &\cssId{s49}{\sqrt{(-2-1)^2 + (5-(-3))^2}}\cr &\qquad \cssId{s50}{= \sqrt{(-3)^2 + 8^2}}\cr &\qquad \cssId{s51}{= \sqrt{9 + 64}}\cr &\qquad \cssId{s52}{= \sqrt{73}} \end{align} $$
Question: Does the following formula represent the distance between points $\,(a,b)\,$ and $\,(c,d)\,$? Answer YES or NO. $$\cssId{s56}{\sqrt{(a-c)^2 + (d-b)^2}}$$
Solution: Yes. The order that you subtract the numbers does not affect the result.
Question: Does the following formula represent the distance between points $\,(a,b)\,$ and $\,(c,d)\,$? Answer YES or NO. $$\cssId{s63}{\sqrt{(a-b)^2 + (c-d)^2}}$$
Solution: No. You must subtract the $\,x$-values and $\,y$-values of the two points.

Note: When the number inside a square root has a factor that is a perfect square, then it can be renamed. For example, $\,4\,$ goes into $\,8\,$ evenly, and $\,4\,$ is a perfect square. Thus, we can rename as follows: $$ \cssId{s72}{\sqrt{8}} \cssId{s73}{= \sqrt{4\cdot 2}} \cssId{s74}{= \sqrt{4}\sqrt{2}} \cssId{s75}{= 2\sqrt{2}} $$ In the solutions to this web exercise, both names ($\,\sqrt{8}\,$ and $\,2\sqrt{2}\,$) are given.

Concept Practice