 Locating Points in Quadrants and on Axes
Locating Points in Quadrants and on Axes
An ordered pair $\,(x,y)\,$ is a pair of numbers, separated by a comma, and enclosed in parentheses. The order that the numbers are listed makes a difference: $\,(5,3)\,$ is different from $\,(3,5)\,.$ Thus, the name ordered pair is appropriate.
The number that is listed first is called the first coordinate or the $x$-value. The number that is listed second is called the second coordinate or the $y$-value.
For example, $\,(5,3)\,$ is an ordered pair: the first coordinate is $\,5\,$ and the second coordinate is $\,3\,.$ Alternatively, the $x$-value is $\,5\,$ and the $y$-value is $\,3\,.$
Partial translation: For two ordered pairs to be equal, the first coordinates must be equal, and the second coordinates must be equal.
The coordinate plane (also called the $\,xy$-plane) is a device to ‘picture’ ordered pairs. Each ordered pair corresponds to a point in the coordinate plane, and each point in the coordinate plane corresponds to an ordered pair. For this reason, ordered pairs are often called points.
The process of showing where a point ‘lives’ in a coordinate plane is called plotting the point. To plot the point $\,(1,-2)\,$:
- Start at the point $\,(0,0)\,$ (look at the diagram below).
- Move $\,1\,$ to the right.
- Move down $\,2\,.$
To plot the point $\,(-2,1)\,$:
- Start at the point $\,(0,0)\,.$
- Move $\,2\,$ to the left.
- Move up $\,1\,.$
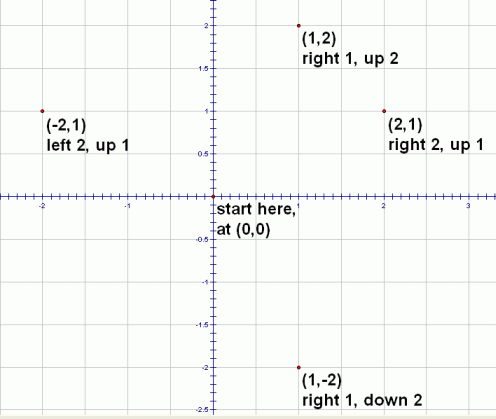
Notice that the $x$-value tells you how to move left/right: if the $x$-value is positive, move right; if the $x$-value is negative, move left.
Notice that the $y$-value tells you how to move up/down: if the $y$-value is positive, move up; if the $y$-value is negative, move down.
The quadrants (see below) divide the coordinate plane into four regions.
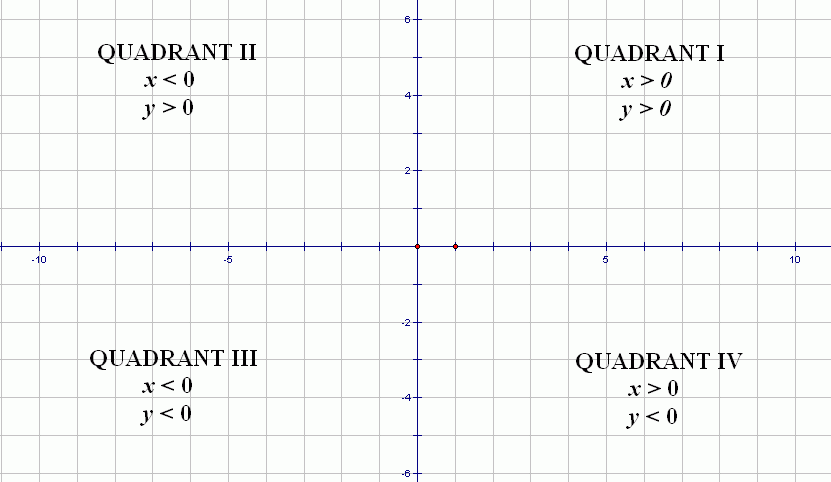
Quadrant I is the set of all points $\,(x,y)\,$ with $\,x\gt 0\,$ and $\,y\gt 0\,.$
Quadrant II is the set of all points $\,(x,y)\,$ with $\,x\lt 0\,$ and $\,y\gt 0\,.$
Quadrant III is the set of all points $\,(x,y)\,$ with $\,x\lt 0\,$ and $\,y\lt 0\,.$
Quadrant IV is the set of all points $\,(x,y)\,$ with $\,x\gt 0\,$ and $\,y\lt 0\,.$
Roman numerals (I, II, III, IV) are conventionally used to talk about the four quadrants. You start numbering the quadrants in the upper right, and then proceed counter-clockwise.
The $x$-axis is the set of all points $\,(x,0)\,,$ for all real numbers $\,x\,.$ The $x$-axis is the horizontal axis (think of the horizon). The $x$-axis separates the upper two quadrants (I and II) from the bottom two quadrants (III and IV). Points on the $x$-axis do not belong to any quadrant.
The $y$-axis is the set of all points $\,(0,y)\,,$ for all real numbers $\,y\,.$ The $y$-axis is the vertical axis. The $y$-axis separates the right two quadrants (I and IV) from the left two quadrants (II and III). Points on the $y$-axis do not belong to any quadrant.
The origin is the point $\,(0,0)\,.$ The origin is the only point that lies on both the $x$-axis and the $y$-axis.
Points with positive $x$-values lie to the right of the $y$-axis.
Points with negative $x$-values lie to the left of the $y$-axis.
Points with positive $y$-values lie above the $x$-axis.
Points with negative $y$-values lie below the $x$-axis.