audio read-through Review of Quadratic Functions: Vertex Form, Max/Min, Intercepts, More

 

DEFINITION quadratic function (standard form; vertex form)

Let $\,a\,,$ $\,b\,$ and $\,c\,$ be real numbers, with $\,a \ne 0\,.$

A quadratic function is a function that can be written in the form $\,y = ax^2 + bx + c\,.$ This is called the standard form of the quadratic function.

Every quadratic function can also be written in the form $\,y=a{(x-h)}^2 + k\,.$ This is called the vertex form of the quadratic function.

For a thorough review of quadratic functions, including going from standard to vertex form, read Quadratic Functions and the Completing the Square Technique.

Summary: Properties of Quadratic Functions

GRAPH

$y = ax^2 + bx + c\,$:
(standard form)
($a\ne 0$)

Every quadratic function graphs as a parabola, which has beautiful and important reflecting properties.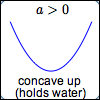

concave up parabola
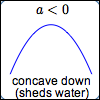
concave down parabola

If you want to know the focus and directrix of $\,y = a(x-h)^2 + k\,,$ read Equations of Simple Parabolas.

$y = a(x-h)^2 + k\,$:
(vertex form)
($a\ne 0$)
Comments:

For $\,a \gt 0\,,$

$$ \cssId{s22}{\underbrace{a(x-h)^2}_{\ge 0} + k \overset{\text{always!}}{\ge} k} $$

Thus, $\,k\,$ is a global minimum value.

For $\,a \lt 0\,,$

$$ \cssId{s25}{\underbrace{a(x-h)^2}_{\le 0} + k \overset{\text{always!}}{\le} k} $$

Thus, $\,k\,$ is a global maximum value.

VERTEX (Turning Point)

$y = ax^2 + bx + c\,$:
(standard form)
($a\ne 0$)

Let $\,f(x) = ax^2 + bx + c\,,$ with $\,a\ne 0\,.$ The vertex is:

$$ \cssId{s29}{\left(-\frac{b}{2a}\ ,\ f\bigl(-\frac{b}{2a}\bigr)\right)} $$

This is sometimes called the vertex formula, and is worth memorizing. It can be derived by completing the square; or, it's really easy with a bit of calculus!

$y = a(x-h)^2 + k\,$:
(vertex form)
($a\ne 0$)

The vertex is: $(h,k)$

Note how easy it is to get the vertex from this form! Hence, the name ‘vertex form’ is appropriate.

Comments: There is a horizontal tangent line at the vertex.

$y$-INTERCEPT

$y = ax^2 + bx + c\,$:
(standard form)
($a\ne 0$)

When $\,x = 0\,$:

$$\begin{align} y &= a\cdot 0^2 + b\cdot 0 + c\cr &= c \end{align} $$
$y = a(x-h)^2 + k\,$:
(vertex form)
($a\ne 0$)

When $\,x = 0\,$:

$$\begin{align} y &= a(0 - h)^2 + k\cr &= ah^2 + k \end{align}$$
Comments: To find where a graph crosses the $y$-axis, set $\,x = 0\,$ and solve for $\,y\,.$

$x$-INTERCEPT(S)

$y = ax^2 + bx + c\,$:
(standard form)
($a\ne 0$)

Use the Quadratic Formula, as needed:

$ax^2 + bx + c = 0\ $ and $\ a\ne 0$

is equivalent to

$\displaystyle x = \frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$

exactly one x-intercept

$b^2 - 4ac = 0\,$
Exactly one $x$-intercept

$ax^2 + bx + c = 0$
has exactly one real number solution.

exactly one x-intercept

$b^2 - 4ac \gt 0$
Two different $x$-intercepts

$ax^2 + bx + c = 0$
has two different real number solutions.

exactly one x-intercept

$b^2 - 4ac \lt 0$
No $x$-intercepts

$ax^2 + bx + c = 0$
has no real number solutions.
It has two different complex number solutions.

$y = a(x-h)^2 + k\,$:
(vertex form)
($a\ne 0$)

Easiest: isolate the squared expression; correctly ‘undo’ the square.

Example:

$$ \begin{gather} \cssId{s66}{0 = 2(x-1)^2 -5}\cr\cr \cssId{s67}{5 = 2(x-1)^2}\cr\cr \cssId{s68}{\frac 52 = (x-1)^2}\cr\cr \cssId{s69}{x-1 = \pm\sqrt{\frac{5}{2}}} \cr\cr \cssId{s70}{x = 1\pm\sqrt{\frac{5}{2}}} \end{gather} $$

Need help with the last couple steps? Study:

Comments: To find where a graph crosses the $x$-axis, set $\,y = 0\,$ and solve for $\,x\,.$

Use the following Wolfram Alpha widgets to graph and compute properties of quadratic functions. After pressing ‘Submit’ be sure to scroll down to see the graphs!

Concept Practice