Complex Numbers

In the previous section, The Quadratic Formula, we saw that quadratic equations may have:

two different real number solutions;
exactly one real number solution; or
no real number solutions.

For example, the simple quadratic equation $\,x^2 = -1\,$ has no real number solutions since there is no real number which, when squared, gives $\,-1\,.$

By introducing just one new number (which we'll call $\,i\,$—think ‘$i$maginary’) we'll generate a set of numbers called the complex numbers which are extremely important in mathematics and engineering.

First, a definition:

DEFINITION the imaginary number $\,i\,$

Define a number $\,i\,$ as follows: $$ \cssId{s14}{i := \sqrt{-1}}\ , $$ so that $$ \cssId{s16}{i^2 = -1}\ . $$

Notice that $\,i\,$ is not a real number, since no real number, when squared, gives $\,-1\,.$

So, $\,i\,$ can't live on the real number line, since it's not a real number. We need to give $\,i\,$ a place to live! It lives one unit up from $\,0\,$ on the real number line, as in the sketch below:

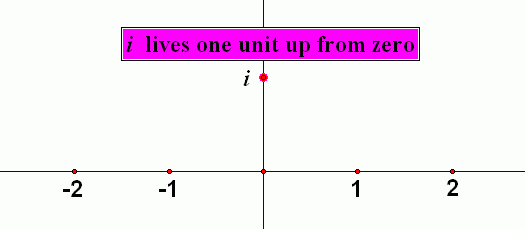
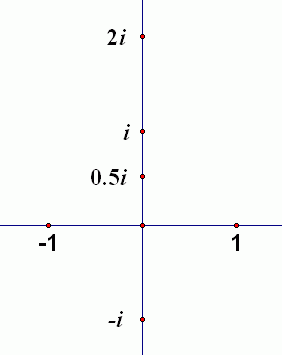
Now, all the scalar multiples of $\,i\,$ will live along the vertical axis, as shown below. Therefore, this vertical axis is called the imaginary axis. The horizontal axis (where the real numbers live) is called the real axis.

Names are now given to all the numbers that live off the imaginary and real axes. As shown below, the intersection of the vertical line through $\,2\,$ on the real axis and the horizontal line through $\,i\,$ on the imaginary axis is given the name $\,2 + i\,.$

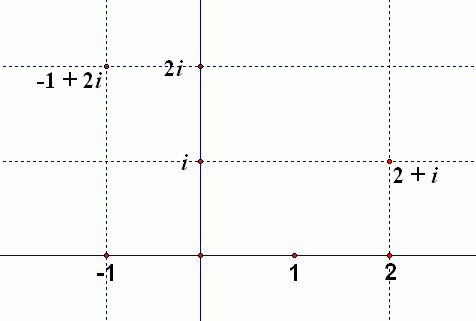
Equivalently, you can think of it this way: start at the origin, go $\,2\,$ to the right, and up $\,1\,.$ You arrive at the number $\,2 + 1i = 2 + i\,.$

Or, go to the left $\,1\,$ and up $\,2\,$ to arrive at the number $\,-1 + 2i\,.$

Note that the left/right movement tells you the real part of the number, and the up/down movement tells you the imaginary part of the number.

We now have an entire plane of numbers, which is called the set of complex numbers. This plane, which provides a picture of the set of complex numbers, is called the complex plane. The precise definition is given below:

DEFINITION the complex numbers

A complex number is a number of the form $\,a+bi\,,$ where $\,a\,$ and $\,b\,$ are both real numbers, and $\,i = \sqrt{-1}\,.$

The number $\,a\,$ is called the real part of the complex number $\,a+bi\,.$

The number $\,b\,$ is called the imaginary part of the complex number $\,a+bi\,.$

Recall that a real number line is a conceptually perfect picture of the real numbers: every real number corresponds to a point on the line, and every point on the line corresponds to a real number. Thus, there is a one-to-one correspondence between the set of real numbers and points on a real number line.

Similarly, the complex plane is a conceptually perfect picture of the set of complex numbers: every complex number corresponds to a point in the plane, and every point in the plane corresponds to a complex number. There is a one-to-one correspondence between the set of complex numbers and points in the complex plane.

Note that every real number is a complex number: $\,a=a+0i\,.$ The imaginary part of a real number is $\,0\,.$

However, there are lots of complex numbers that are not real numbers! Any complex number that lies either above or below the real axis is not a real number.

Whenever you get a new type of expression, you need to develop tools for working with it. In particular, you need to know conditions under which two expressions get to be called ‘equal’.

For example, two real numbers are equal when they live at precisely the same location on a real number line: e.g., $\frac{11}{2} = 5.5\,.$

Or, two sets are equal when they have precisely the same members: e.g., $\,\{1,2\} = \{2,1\}\,.$

Or, two matrices are equal when they have the same size, and corresponding entries are equal: for example: $$ \begin{bmatrix} 1 & 2\cr 3 & 4 \end{bmatrix} = \begin{bmatrix} \frac{\pi}{\pi} & 1.9+0.1\cr \frac{6}{2} & 2^2 \end{bmatrix} $$

So, under what condition do two complex numbers get to be called equal?

Two complex numbers are equal precisely when they have the same real and imaginary parts:

DEFINITION equality of complex numbers

For all real numbers $\,a\,,$ $\,b\,,$ $\,c\,$ and $\,d\,$:

$$ \begin{gather} \cssId{s62}{a+bi=c+di}\cr \cssId{s63}{\text{if and only if}}\cr \cssId{s64}{a=c\ \text{and}\ b = d} \end{gather} $$

Don't underestimate the power of complex numbers! Real-life problems use non-real numbers and get real number answers!

For example, electrical engineers would find their lives really difficult if they couldn't use complex numbers (although they use $\,j\,$ to denote $\,\sqrt{-1}\,,$ since they already use $\,i\,$ for something else).

I like to use the following analogy to make it plausible that having all the complex numbers to work with is a good thing.

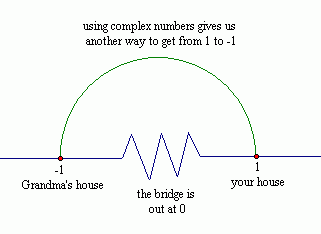
Suppose you live at $\,1\,$ on the real number line, and your grandmother lives at $\,-1\,.$ If the only way to get from your house to her house is along the real number line, and the bridge is out at $\,0\,,$ then (alas) you won't get to visit her.

But, if you have another route (moving around in the complex plane) then you can still visit her! Woo hoo! So, in a sense, the complex plane gives you room to move, which offers additional flexibility in solving problems.