Logarithm Summary: Properties, Formulas, Laws

Logarithms and logarithmic functions have been thoroughly covered in:

• Introduction to Logarithms
• Properties of Logarithms
• Change of Base Formula for Logarithms
• Introduction to Logarithmic Functions
• Logarithmic Functions: Review and Additional Properties

This section provides an in-a-nutshell, at-a-glance summary of key results.

What is $\,\log_b x\,$?

Logarithms are exponents! The number  ‘$\,\log_b x\,$’  is the power (the exponent) that $\,b\,$ must be raised to, in order to get $\,x\,.$

Read  ‘$\,\log_b x\,$’  as  ‘log base $\,b\,$ of $\,x\,$’.

The equation  ‘$\,\log_b x = y\,$’  is called the logarithmic form of the equation.

The equation  ‘$\,b^y = x\,$’  is called the exponential form of the equation.

Examples:

$\log_2 8 = 3\ $ since $\ 2^3 = 8$

$\log_7 1 = 0\ $ since $\ 7^0 = 1\,$

$\log_3 \frac 13 = -1\ $ since $\ 3^{-1} = \frac 13$

Allowable Bases For Logs

In the expression  ‘$\,\log_b x\,$’ , the number $\,b\,$ is called the base of the logarithm. The number $\,b\,$ must be positive and not equal to $\,1\,$:  $\,b \gt 0\,$ and $\,b\ne 1\,.$

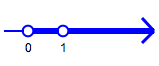
Allowable Bases For Logarithms:
$b \gt 0\,,$ $\,b\ne 1$

Two Special Logarithms

The function  ‘$\,\log_{10}$’   (log base $10$) is called the common logarithm. It is often abbreviated as just  ‘$\,\log\,$’  (with no indicated base).

The function  ‘$\,\log_{\text{e}}$’   (log base $\,\text{e}\,$) is called the natural logarithm. It is often abbreviated as  ‘$\,\ln\,$’   (with no indicated base).

Caution: Some disciplines use  ‘$\,\log\,$’  to mean the natural logarithm. Always check notation.

Summary:

$\log x\,$:  the common log of $\,x$

$\ln x\,$:  the natural log of $\,x$

Allowable Inputs For Logs

In the expression  ‘$\,\log_b x\,$’, the number $\,x\,$ (the input) must be positive: $\,x \gt 0\,.$

Allowable Inputs For Logarithms:
$x \gt 0$

Function View of Logs

The number  ‘$\log_b x\,$’  is the output from the function  ‘$\,\log_b\,$’  when the input is  ‘$\,x\,$’.

The domain of the function $\,\log_b\,$ is the set of all positive real numbers:   $\,\text{dom}(\log_b) = (0,\infty)$

The range of the function $\,\log_b\,$ is the set of all real numbers:   $\,\text{ran}(\log_b) = \Bbb R$

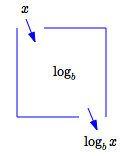
Function View Of Logarithms

Laws of Logarithms

Let $\,b\gt 0\,,$ $\,b\ne 1\,,$ $\,x\gt 0\,,$ and $\,y\gt 0\,.$

$\log_b\,xy = \log_b x + \log_b y$
The log of a product is the sum of the logs.

$\displaystyle \log_b\frac{x}{y} = \log_b x - \log_b y$
The log of a quotient is the difference of the logs.

For this final property, $\,y\,$ can be any real number:

$\log_b\,x^y = y\,\log_b x$
You can bring exponents down.

See Properties of Logarithms for a typical proof of these laws.

Change of Base Formula for Logarithms

Let $\,a\,$ and $\,b\,$ be positive numbers that are not equal to $\,1\,,$ and let $\,x\gt 0\,.$ Then:

In words: You can change from any base $\,b\,$ to any base $\,a\,$; the ‘adjustment’ is that you must divide by the log to the new base ($\,a\,$) of the old base ($\,b\,$).

See Change of Base Formula for Logarithms for a derivation of this formula.

The equation

shows that any log curve is just a vertical scaling of any other log curve!

Logarithm Functions Are One-to-One

Since logarithms are functions:

$x = y \ \ \Rightarrow\ \ \log_b x = \log_b y$
When inputs are the same, outputs are the same.

Since logarithms are one-to-one:

$\log_b x = \log_b y\ \ \Rightarrow\ \ x = y$
When outputs are the same, inputs are the same.

Thus, for all $\,b \gt 0\,,$ $\,b\ne 1\,,$ $\,x \gt 0\,$ and $\,y \gt 0\,$:

Inverse Properties

Logarithmic functions are one-to-one, hence have inverses.

The inverse of the logarithmic function with base $\,b\,$ is the exponential function with base $\,b\,.$

For $\,b \gt 0\,,$ $\,b\ne 1\,,$ and all real numbers $\,x\,$:

For $\,b \gt 0\,,$ $\,b \ne 1\,,$ and $\,x \gt 0\,$:

Special Points

For $\,b \gt 0\,$ and $\,b\ne 1\,$:

• $\log_b b = 1\,$  (since $\,b^1 = b\,$)

  Equivalently, the point $\,(b,1)\,$ lies on the graph of $\,y = \log_b x\,.$

• $\log_b 1 = 0\,$  (since $\,b^0 = 1\,$)

  Equivalently, the point $\,(1,0)\,$ lies on the graph of $\,y = \log_b x\,.$

Graphs of Logarithmic Functions

Properties shared by all logarithmic graphs, $\,y = \log_b x\,$:

• Vertical asymptote: $\,x = 0$
• Pass both horizontal and vertical line tests
• Contain the point $\,(1,0)\,$
• Contain the point $\,(b,1)\,$
• Domain is the set of all positive real numbers
• Range is the set of all real numbers
• The inverse of  $\,y = \log_b x\,$  is  $\,y = b^x$
• The graph of the inverse is shown in red on the graphs below: the inverse is the reflection of the logarithmic graph about the line $\,y = x\,.$

For $\,b \gt 1\,$:

• $y = \log_b x\,$ is an increasing function: $$\cssId{s98}{x \lt y\ \ \iff\ \ \log_b x \lt \log_b y}$$
• Right-hand end behavior:  as $\,x\rightarrow\infty\,,$ $\,y\rightarrow\infty$
• $\,x = 0\,$ is a vertical asymptote:  as $\,x\rightarrow 0^{+}\,,$ $\,y\rightarrow -\infty\,$

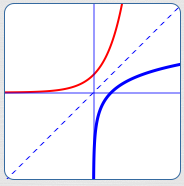
$\,b \gt 1\,$:
Blue curve: $\,y = \log_b x$
Red curve: inverse $\,y = b^x$
Dashed line: $\,y = x$

For $\,0 \lt b \lt 1\,$:

• $y = \log_b x\,$ is a decreasing function: $$\cssId{s109}{x \lt y\ \ \iff\ \ \log_b x \gt \log_b y}$$
• Right-hand end behavior:  as $\,x\rightarrow\infty\,,$ $\,y\rightarrow -\infty$
• $\,x = 0\,$ is a vertical asymptote:  as $\,x\rightarrow 0^{+}\,,$ $\,y\rightarrow \infty$

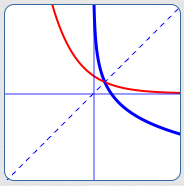
$\,0 \lt b \lt 1\,$:
Blue curve: $\,y = \log_b x\,$
Red curve: inverse $\,y = b^x\,$
Dashed line: $\,y = x\,$