Introduction to Logarithmic Functions (Part 1)

(This page is Part 1. Click here for Part 2.)

Before doing this exercise, you may want to review basic properties of logarithms:

In this section we continue to explore logarithms, but now with an emphasis on the family of logarithmic functions.

DEFINITION logarithmic function

A logarithmic function is a function of the form $\,y=\log_b\,x\,,$ where $\,b\,$ is a positive number not equal to $\,1\,,$ and $\,x\gt 0\,.$

The number $\,b\,$ is called the base of the logarithm.

When the base is $\,\text{e}\,,$ the function is called the natural logarithm, and can be written as $\,y=\ln\,x\,.$

(Note: $\,\text{e}\approx 2.71828\,$)

When the base is $\,10\,,$ the function is called the common logarithm, and can be written as $\,y=\log\,x\,.$

Be Alert to Differences in Notation

Some academic disciplines use the natural log a lot, but the common log not so much. These disciplines often use $\,\log\,$ to mean log base e, instead of log base ten. Be sure to check what notation is being used whenever you start communicating with someone new.

Furthermore, some mathematicians (this author included) tend to call more general functions where a logarithm is acting on variable input a logarithmic function: say, $\,y=\ln (2x-3)\,$ or $\,y=-7\log(5-x)\,.$ For the purposes of this section, however, the phrase logarithmic function refers only to functions of the form $\,y=\log_b\,x\,.$

There are two basic shapes to the graphs of logarithmic functions, depending on whether the base is greater than $\,1\,,$ or between $\,0\,$ and $\,1\,$:

$\,y=\log_b\,x\,$ for $\,b\gt 1\,$

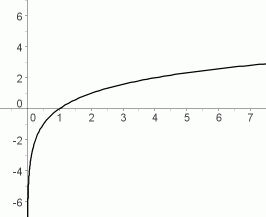
increasing functions

$\,y=\log_b\,x\,$ for $\,0\lt b\lt 1\,$

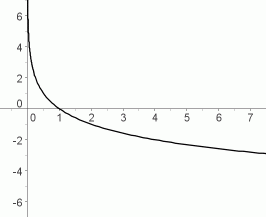
decreasing functions

Properties of the Graph for $\,b\gt 1$

An increasing function has the following property: as you walk along the graph, going from left to right, you are always going uphill.

The following are equivalent for a function $\,f(x)=\log_b\,x\,$:

$\,f\,$ is an increasing function
$\,b\gt 1\,$

For increasing logarithmic functions:

as $\,x\rightarrow\infty\,,$ $\,y\rightarrow\infty\,$

Read this aloud as: as $\,x\,$ goes to infinity, $\,y\,$ goes to infinity

This is the right-hand end behavior: as we move farther and farther to the right on the graph, the $y$-values of the points are increasing, without bound.

For example, want to get to a point on the graph that is (say) one million units above the $x$-axis? You can do it—but you'll have to go a lloonngg way to the right, because the function increases very slowly.
as $\,x\rightarrow 0^+\,,$ $\,y\rightarrow -\infty\,$

Read this aloud as: as $\,x\,$ approaches zero from the right-hand side, $\,y\,$ goes to negative infinity

For additional practice with sentences like ‘as $\,x\rightarrow\infty\,,$ $\,y\rightarrow\infty\,$’ and ‘as $\,x\rightarrow 0^+\,,$ $\,y\rightarrow -\infty\,$’, you may want to review Basic Models You Must Know.

$y = \log_b\,x\,$ for $\,b\gt 1$
increasing functions
as $\,x\rightarrow\infty\,,$ $\,y\rightarrow\infty\,$
as $\,x\rightarrow 0^+\,,$ $\,y\rightarrow -\infty\,$

Properties of the Graph for $\,0 \lt b\lt 1$

A decreasing function has the following property: as you walk along the graph, going from left to right, you are always going downhill.

The following are equivalent for a function $\,f(x)=\log_b\,x\,$:

$\,f\,$ is a decreasing function
$\,b\,$ is between $\,0\,$ and $\,1\,$

For decreasing logarithmic functions:

as $\,x\rightarrow\infty\,,$ $\,y\rightarrow -\infty\,$

Read this aloud as: as $\,x\,$ goes to infinity, $\,y\,$ goes to negative infinity
as $\,x\rightarrow 0^+\,,$ $\,y\rightarrow \infty\,$

Read this aloud as: as $\,x\,$ approaches zero from the right-hand side, $\,y\,$ goes to infinity

$y = \log_b\,x\,$ for $\,0 \lt b\lt 1$
decreasing functions
as $\,x\rightarrow\infty\,,$ $\,y\rightarrow -\infty\,$
as $\,x\rightarrow 0^+\,,$ $\,y\rightarrow \infty\,$