Basic Models You Must Know (Part 1)
Basic Models You Must Know (Part 1)
(This page is Part 1. Click here for Part 2.)
Need some basic information on graphs of functions first? Graphs of Functions
There are a handful of functions that you need to have on your fingertips, in the following sense:
- Given the function, you should immediately be able to sketch its graph (indicating all important features).
- Given the graph, you should immediately recognize the (probable) function.
The purpose of this section is to give you practice with these basic models, which will be used freely throughout the rest of the course. (A few more ‘basic models’ will be added in future lessons.)
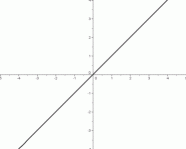
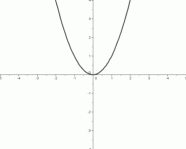
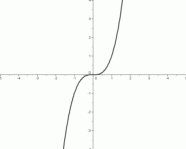
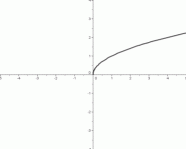
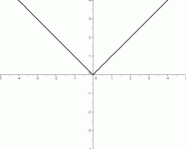
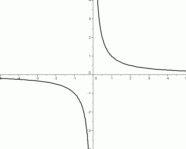
Here are the seven ‘basic models’ to be studied in this lesson (in Part 2). Each is shown in the same window, from $\,-5\,$ to $\,5\,$ on the $x$-axis, and from $\,-4\,$ to $\,4\,$ on the $y$-axis.
The scales on the $x$-axis and $y$-axis are identical. That is, a distance of $\,1\,$ on the $x$-axis is the same as a distance of $\,1\,$ on the $y$-axis.
Reading Domain and Range from a Graph
You may want to review Domain and Range of a Function from the Algebra I curriculum. Key concepts are repeated here for your convenience.
The domain of a function is the set of all its allowable inputs. The domain convention states that if the domain of a function is not specified, then it is assumed to be the set of all real numbers for which the function is defined. The domain of a function $\,f\,$ is denoted by $\,\text{dom}(f)\,.$
The range of a function is the set of all its outputs, as the inputs vary through the entire domain. The range of a function $\,f\,$ is denoted by $\,\text{ran}(f)\,.$
Since the domain and range are sets, correct set notation must be used when reporting them; it may be helpful to review interval and list notation.
Remember that the symbol $\,\mathbb{R}\,$ denotes the set of real numbers.
The domain of a function is usually easy to determine from a formula for the function:
- Numbers that cause division by zero must be excluded from the domain.
- Anything inside an even root (square root, fourth root, etc.) must be greater than or equal to zero.
However, the range of a function is usually more difficult to determine from a formula.
It is easy to get both the domain and range of a function from its graph, as discussed next.
Finding the Domain of a Function from its Graph
Consider the graph shown below: this is the absolute value function, with a restricted domain.
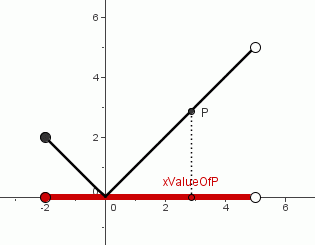
As always, a typical point on the graph is an (input,output) pair; the $\,x$-value of the point is the input, and the $\,y$-value of the point is the output.
As the point $\,P\,$ is moved through the entire graph, all the $\,x$-values indicated in red are taken on. These are the allowable inputs for this function. Therefore, the domain of this function is the interval $\,[-2,5)\,.$
Notice that $\,-2\,$ is in the domain of the function, indicated by the opening ‘$\,[\,$’ in interval notation. However, $\,5\,$ is not in the domain of the function, indicated by the closing ‘$\,)\,$’ in interval notation.
To find the domain of a function from its graph, just ‘collapse’ each point, in its own ‘vertical channel’, into the $\,x\,$-axis.
Finding the Range of a Function from its Graph
Now consider the same graph again, but this time focusing attention on the outputs, which are the $\,y$-values of the points.
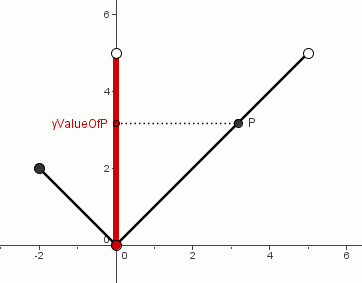
As the point $\,P\,$ is moved through the entire graph, all the $\,y$-values indicated in red are taken on. These are the outputs for this function, as the inputs vary through the entire domain. Therefore, the range of this function is the interval $\,[0,5)\,.$
Notice that $\,0\,$ is in the range of the function, indicated by the opening ‘$\,[\,$’ in interval notation. However, $\,5\,$ is not in the range of the function, indicated by the closing ‘$\,)\,$’ in interval notation.
To find the range of a function from its graph, just ‘collapse’ each point, in its own ‘horizontal channel’, into the $\,y\,$-axis.