 Reflecting Property of a Hyperbola (Part 1)
Reflecting Property of a Hyperbola (Part 1)
(This page is Part 1. Click here for Part 2.)
Hyperbolas were introduced in four prior lessons:
- Introduction to Conic Sections
- Definition of a Hyperbola
- Equations of Hyperbolas in Standard Form
- Graphing Hyperbolas
Hyperbolas (like all conic sections) have an interesting and useful reflecting property. In-a-nutshell: outside light aimed at one focus of the hyperbola is reflected towards the other focus.
The purpose of the current section is to explore and understand this reflecting property of a hyperbola.
Reflecting Property of a Hyperbola
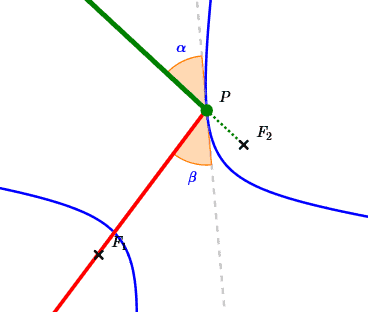
In a hyperbola:
You can play with this reflecting property below:
Points $F_1\,$ and $\,F_2\,$ are the foci of the hyperbola. They can be dragged to change the shape of the hyperbola.
Point $\,C\,$ can also be dragged to change the shape of the hyperbola. (It controls the hyperbola constant.)
Light from outside the hyperbola that is directed towards $\,F_2\,$ hits the hyperbola at point $\,\color{green}{P}\,.$ Point $\,P\,$ can be dragged around the hyperbola.
The dashed grey line is the tangent to the hyperbola at point $\,P\,.$
As discussed in this earlier section, the physics Law of Reflection states that reflected light always makes equal angles with the tangent line.
Observe that the reflected light always passes through $\,F_1\,$!
This reflecting property has practical applications in optics and navigation.
Why Does the Hyperbola Reflecting Property Work?
The bulk of this section is devoted to understanding why the reflecting property works. We'll use trigonometry and also borrow a result from calculus. The idea is simple, but (as you'll see) carrying it out requires some fortitude!
A few preliminary results are needed:
Trigonometric Identity: Tangent of a Difference
For all real numbers $\,x\,$ and $\,y\,$ with $\,\cos(x-y)\ne 0\,,$
$$ \cssId{s32}{\tan(x-y) = \frac{\tan x - \tan y}{1 + \tan x\tan y}} $$Proof
We want a formula that involves $\,\tan x := \frac{\sin x}{\cos x}\,$ and $\,\tan y := \frac{\sin y}{\cos y}\,.$ This fact motivates the form of ‘$\,1\,$’ that we multiply by in the re-naming below:
$$ \begin{align} &\cssId{s36}{\tan(x-y)}\cr\cr &\quad \cssId{s37}{= \frac{\sin(x-y)}{\cos(x-y)}}\cr &\qquad \cssId{s38}{\text{(Definition of tangent)}}\cr\cr &\quad \cssId{s39}{= \frac{\sin x\cos y - \cos x\sin y}{\cos x\cos y + \sin x\sin y}}\cr &\qquad \cssId{s40}{\text{(Difference formulas for sine and cosine)}}\cr\cr &\quad \cssId{s41}{= \frac{\sin x\cos y - \cos x\sin y}{\cos x\cos y + \sin x\sin y}\cdot\frac{\frac{1}{\cos x\cos y}}{\frac{1}{\cos x\cos y}}}\cr &\qquad \cssId{s42}{\text{(Multiply by $\,1\,$)}}\cr\cr &\quad \cssId{s43}{= \frac{\frac{\sin x\color{red}{\cos y}}{\cos x\color{red}{\cos y}} - \frac{\color{red}{\cos x}\sin y}{\color{red}{\cos x}\cos y}}{\frac{\color{red}{\cos x\cos y}}{\color{red}{\cos x\cos y}} + \frac{\sin x\sin y}{\cos x\cos y}}}\cr &\qquad \cssId{s44}{\text{(Distributive law)}}\cr\cr &\quad \cssId{s45}{= \frac{\tan x - \tan y}{1 + \tan x\tan y}}\cr &\qquad \cssId{s46}{\text{(Cancel, definition of tangent)}} \end{align} $$ QEDAngle of Inclination of a Line
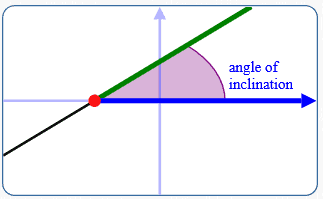
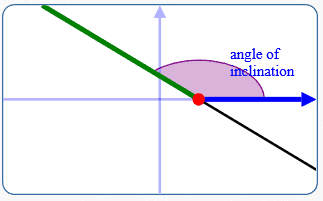
The angle of inclination of a horizontal line equals zero.
For non-horizontal lines:
Every non-horizontal line in an $xy$-plane intersects the $x$-axis in a unique point. This intersection point splits both the line and the $x$-axis:
- The line has a part above and below the $x$-axis
- The $x$-axis has a part to the right and to the left of the intersection point
The (nonnegative) measure of the angle between:
- The part of the line above the $x$-axis
- The part of the $x$-axis to the right of the intersection point
is the angle of inclination of the line .
Note
Angle of inclination is always in the interval:
- $[0,180^\circ)\,$ (for degree measure)
- $[0,\pi)\,$ (for radian measure)
Relationship Between Slope and Angle of Inclination of a Line
Note: If you are visually relating slope and angle of inclination of a line, be sure that ‘$\,1\,$’ on the $x$-axis is the same as ‘$\,1\,$’ on the $y$-axis. Otherwise, uncomfortable things can happen!
For example, suppose ‘$\,1\,$’ on the $x$-axis is one mile to the right of zero, but ‘$\,1\,$’ on the $y$-axis is just one inch up from zero. Then, a line with slope $\,1\,$ appears to have an angle of inclination close to zero (instead of $\,45^\circ\,$)!
Or, suppose ‘$\,1\,$’ on the $y$-axis is one mile up from zero, but ‘$\,1\,$’ on the $x$-axis is just one inch to the right of zero. Then, a line with slope $\,1\,$ appears to have an angle of inclination close to $\,90^\circ\,$ (instead of $\,45^\circ\,$)!
Fact: If $\,\alpha\,$ is the angle of inclination of any non-vertical line with slope $\,m\,,$ then:
$$\cssId{s78}{\tan\alpha = m}$$In words: the tangent of the angle of inclination of a line equals the slope of the line.
Why? (Proof of Fact)
Horizontal Line
$\,\alpha = 0\,$ and $\,m = 0\,$
Thus, $\,\tan\alpha = \tan 0 = 0 = m\,.$
Line with Positive Slope
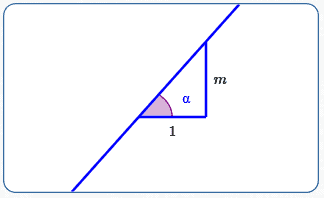 $$\tan(\text{angle of inclination}) = \text{slope of line}$$
$$\tan(\text{angle of inclination}) = \text{slope of line}$$
(See sketch above.) Here, $\,m > 0\,.$ Thus, $\,\tan\alpha = \frac{\text{opp}}{\text{adj}} = \frac{m}{1} = m\,.$
Line with Negative Slope
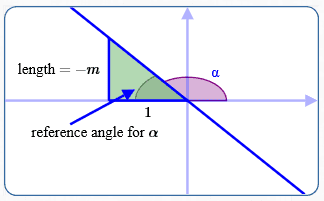 $$\tan(\text{angle of inclination}) = \text{slope of line}$$
$$\tan(\text{angle of inclination}) = \text{slope of line}$$
(See sketch above.) Here, $\,m \lt 0\,,$ so $\,-m \gt 0\,.$
Using the reference angle for $\,\alpha\,$ (in the green triangle), the size of $\,\tan\alpha\,$ is $\, \frac{\text{opp}}{\text{adj}} = \frac{-m}{1} = -m\,.$
Since $\,\alpha\,$ is in the second quadrant, the sign of $\,\tan\alpha\,$ is negative.
Thus:
$$ \cssId{s97}{\tan \alpha = \overbrace{(-)}^{\text{sign}}\overbrace{(-m)}^{\text{size}} = m} $$Vertical Line
Note: For a vertical line, the angle of inclination is $\,\alpha = 90^\circ\,.$ In this case, both slope and $\,\tan\alpha\,$ are undefined.
Finally, we need a formula for:
Finding the (Tangent of the) Angle Between Two Intersecting Lines of Known Slope
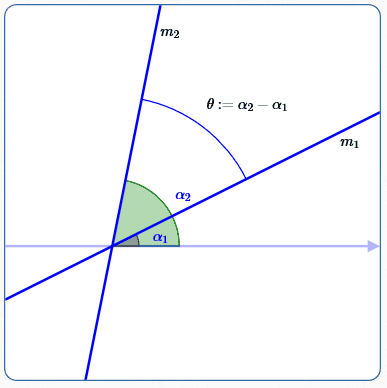 $$
\tan\theta = \frac{m_2 - m_1}{1 + m_2m_1}
$$
$$
\tan\theta = \frac{m_2 - m_1}{1 + m_2m_1}
$$
(The line with the greater angle of inclination has slope $\,m_2\,.$)
Suppose two non-vertical lines with known slopes intersect. As illustrated above:
- Let $\,\alpha_1\,$ and $\,\alpha_2\,$ denote the angles of inclination of the two lines. Re-naming if necessary, assume $\,\alpha_2 \ge \alpha_1\,.$
- Let $\,m_1\,$ be the slope of the line with angle of inclination $\,\alpha_1\,.$
- Let $\,m_2\,$ be the slope of the line with angle of inclination $\,\alpha_2\,.$
- Let $\,\theta\,$ be the angle between the two lines, as shown: $\,\theta := \alpha_2 - \alpha_1$
Then:
$$ \begin{align} &\cssId{s112}{\tan\theta} \cr\cr &\quad\cssId{s113}{= \tan(\alpha_2-\alpha_1)}\cr &\qquad\cssId{s114}{\text{(definition of $\,\theta\,$)}}\cr\cr &\quad\cssId{s115}{= \frac{\tan\alpha_2 - \tan\alpha_1}{1 + \tan\alpha_2\tan\alpha_1}}\cr &\qquad\cssId{s116}{\text{(tangent of a difference)}}\cr\cr &\quad\cssId{s117}{= \frac{m_2 - m_1}{1 + m_2m_1}}\cr &\qquad\cssId{s118}{\substack{\text{(relationship between slope}\cr \text{and angle of inclination)}}} \end{align} $$