Introduction to Conic Sections

One of the things I inherited over my decades of teaching mathematics is a wooden right circular cone.
You can likely tell from the photo (left, below) that it has been well-used and much-loved.

Of course, cones can be oriented in many different ways! To simplify language, in this section we assume cones are oriented as shown below—like an upside-down ice-cream cone sitting on a table.

In this position, a horizontal slice chops off the top of the cone, leaving you looking down at a small circle.

(This sketch is from Wikipedia.)

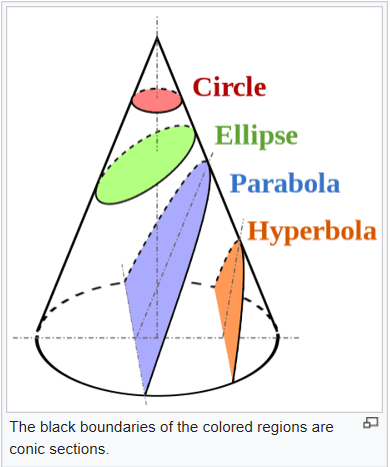
Look at the color-adorned image in the middle, and you'll see the various cuts where parts of my wooden cone can be removed.
As we'll discuss on this page, these ‘slices’ illustrate the conic sections:

horizontal cut near top: a circle
slanted cut just beneath: an ellipse
slice that is parallel to the (yellow) left ‘edge’ of the cone: a parabola
steeper cut: (half of) a hyperbola

When I present this wooden cone to my students, they need a good imagination. Why?
Because what I really want them to envision is this:

A double cone—a pair of these cones, with one stacked over the other, as shown (roughly) at right. (Please excuse my limited photo-editing skills!) The single point where the two cones meet is often called the apex or the vertex.
The double cone should be infinite: it continues up (and down) forever.

In the sections on conics, we'll call this an infinite double cone. Think of it as a sort of infinite hourglass.

There are different ways to define conic sections, but the definition we're using here is this:

Conic sections are curves that are formed by the intersection of a plane with the surface of an infinite double cone.

What does it look like when a plane slices through an infinite double cone?

Most people like to think of the conic sections as:

ellipses (special case: circles)
parabolas
hyperbolas

As you'll see in detail below, these are the three basic shapes you get when you slice a plane through an infinite double cone.

Degenerate Conics

However, if the slicing plane goes through the apex, then weird things can happen!
These resulting intersections are called degenerate conics.

For example, if a horizontal plane passes through the apex, then the intersection is a single point.
How boring! People don't typically want to call a point a conic section!
So, a point is an example of a degenerate conic.

Here's a fantastic youtube video on conic sections.
Its length is 5:27 (five minutes, 27 seconds): if you have limited time, skip the intro/terminology and start at 1:38.
Degenerate conics start at 3:47, and you'll see that there are three types:

a single point (a degenerate ellipse)
a line (a degenerate parabola)
a pair of intersecting lines (a degenerate hyperbola)

So... why the name ‘Conic’?

So, why is the name ‘conic’ or ‘conic section’ appropriate?
Because conics arise by intersecting a plane with an (infinite double) CONE!!

How to Orient the Plane to get Different Conic Sections

Circle

Start with a horizontal plane cutting through the double cone (anywhere except through the apex).

This yields a circle, as shown at right.

The photo is taken looking down from the ‘top’ of a single cone.

Ellipse

Now, start tipping the plane slightly from the horizontal.

This yields an ellipse, as shown at right.

(Someone drew the smiley face on the ellipse before I acquired the wooden cone!)

Parabola

As you continue to tilt the plane, you'll reach an instant when the plane is parallel to the ‘edge/side’ of the cone.

This can be made mathematically precise, but the first image at right should be sufficient. Notice that the board leaning along the edge of the cone is at precisely the same slant as the cut in the wood.

This is the situation that gives a parabola.

Hyperbola

Continue to tilt the plane, so it's getting steeper and steeper (approaching vertical).

Notice (first photo at right) that the cut in the wood is definitely steeper than the board leaning along the side! Indeed, it looks like this particular cut is vertical, but it doesn't need to be—it just needs to be steeper than the side.

This is the situation that gives a hyperbola.

Unlike circles, ellipses, and parabolas, a hyperbola has two pieces—one on each cone. Of course, this wooden cone only shows one of the pieces!

What good are conics?

There are many occurrences of conic shapes in nature and life.
Here are some examples:

Parabola:
Throw a ball into the air. Its path (until it reaches the ground) is parabolic.
Ellipse:
The orbits of the planets around the sun are elliptical.
Hyperbola: [reference, near bottom]
The shock waves created by an airplane traveling faster than the speed of sound is called a sonic boom.
The shock waves make a cone (with the airplane as the apex), and the ground (an approximate plane) intersects this cone in a hyperbola.

Also, conics have special properties that make them valuable tools.
Here are some examples:

Parabola:
There's a special point inside a parabola.
Light emanating from this special point will hit the parabola, and always bounce off in the same direction.
So, a parabola can ‘straighten’ light!
Think lasers or search lights.
Circle:
Given a piece of string, what shape encloses the most area? A circle.
Ellipse:
There are two special points inside an ellipse.
Waves emanating from one point bounce off the ellipse and then go through the other point.
A ‘whispering room’ uses this fact: if people stand at two special places in the room—even though they're far apart and are whispering—they'll be able to hear each other!
Hyperbola:
A hyperbola has two special points associated with it.
For any point on the hyperbola, the difference of the distances to these two special points is always the same.
This property can be exploited to solve navigation problems.

All the reflecting properties will be studied in detail in future sections.

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
identifying conics by the discriminant