 Reflecting Property of an Ellipse (Part 1)
Reflecting Property of an Ellipse (Part 1)
(This page is Part 1. Click here for Part 2.)
Ellipses were introduced in Introduction to Conic Sections, as one of several different curves (‘conic sections’) that are formed by intersecting a plane with an infinite double cone.
The prior section explores the standard definition of an ellipse. The essential ideas are reviewed below for your convenience.
The purpose of this section is to explore the reflecting property of ellipses—that light emitted from one focus is reflected through the other focus.
Review: Definition of an Ellipse
An ellipse is determined by three pieces of information: two points and a number.
The two points are often named $\,F_1\,$ and $\,F_2\,,$ and are called the foci (pronounced FOE-sigh) of the ellipse. (The singular form of foci is focus: one focus, two foci.)
The number is often denoted by $\,k\,$; it must be strictly greater than the distance between the foci. That is, $\,k \gt d(F_1,F_2)\,.$
The ellipse determined by $\,F_1\,,$ $\,F_2\,$ and $\,k\,$ is, by definition, the set of points $\,P\,$ in a plane such that the sum of the distances to the two fixed points is constant:
$$ \cssId{s14}{d(P,F_1) + d(P,F_2) = k} $$Reflecting Property of an Ellipse
In an ellipse:
You can play with this reflecting property below:
(Refresh the page to start over)
- Points $F_1\,$ and $\,F_2\,$ are the foci. They can be dragged to change the shape of the ellipse.
- ‘Light’ is emitted from $\,F_1\,$ (the red segment).
- The light hits the ellipse at point $\,\color{purple}{P}\,.$ (Point $\,P\,$ can be dragged around the ellipse.)
- The light is always reflected so that it passes through $\,F_2\,.$
- Point $\,S\,$ can also be moved to change the shape of the ellipse. (For fixed foci, moving $\,S\,$ changes the ellipse constant.)
Notes
- Drag $\,F_1\,$ to coincide with $\,F_2\,,$ creating a circle. Light emitted from the center hits the circle and is reflected back through the center.
- If (say) a light bulb is placed at $\,F_1\,,$ then light waves go out in all directions at the same time. Click the button to get more (randomly-generated) light! (Refresh the page if you want to start over.)
Two Applications of the Ellipse Reflecting Property
Medicine
Solid material (often referred to as ‘stones’) can sometimes form in the human body, causing serious pain. In the gallbladder, they're called gallstones. In the kidney or urinary tract, they're called kidney stones.
The process called lithotripsy (LITH-oh-trip-see) uses the reflecting property of the ellipse to shatter the stones into tiny pieces, which the body can then get rid of on its own. Shockwaves are emitted from one focus of an ellipse, with the targeted stone located at the other focus.
Architecture
In a whispering gallery or whispering room, quiet sounds (whispers) emitted from one particular place in the room can be clearly heard at another (remote) place.
Different methods can achieve this effect —one method uses a ceiling with elliptical cross-sections (called an ‘ellipsoid’). Note that in a given ellipse, all the reflecting paths from one focus to the other have the same length (the ellipse constant), so sound waves emitted at the same time will also arrive at the same time.
Why Does the Ellipse Reflecting Property Work?
To see why light from one focus is always reflected through the other focus, we need a few ideas. We start by looking at a simple childhood game:
‘Touch the Wall’ Playground Game
This game involves a wall (or fence) and two special spots marked on the ground.
Two or more kids must run from one designated spot ($\,P_1\,$), touch the wall ($\,W\,$), and then run to a second designated spot ($\,P_2\,$). First arriver at $\,P_2\,$ wins the game!
Of course, your running speed matters. But, the distance that you run also matters. To maximize your chances of winning, where should you touch the wall? Does it matter?
You can ‘play with’ this game above:
- Drag point $\,W\,$ along the wall, keeping it between the two yellow points. The red path is the distance you must run; its length is displayed at the top. You'll see that different paths have different lengths.
-
Let $\,m_1\,$ and $\,m_2\,$ denote the measures of the indicated angles:
- $m_1\,$ is the angle between $\,\overline{P_1W}\,$ (the line segment from $\,P_1\,$ to $\,W\,$) and the wall that lies to the left of $\,W$
- $m_2\,$ is the angle between $\,\overline{P_2W}\,$ (the line segment from $\,P_2\,$ to $\,W\,$) and the wall that lies to the right of $\,W$
These angle measures, in degrees, are also displayed.
- By dragging $\,W\,,$ try to make the length of the red path as small as possible. What do you notice about the relationship between $\,m_1\,$ and $\,m_2\,$?
- For another direction: Try to get $\,m_1\,$ as close to $\,m_2\,$ as possible. What do you notice about the length of the red path?
- You can move points $\,P_1\,$ and $\,P_2\,$ to change where the kids start and stop. However, keep $\,P_1\,$ to the left of $\,P_2\,.$
- You can drag the two yellow points to change the location of the wall.
Minimizing the Length of the Path from a Point, to a Line, to a Second Point on the Same Side of the Line
Let's summarize and prove the results of the prior exploration.
Suppose you have a line, and two different points on the same side of the line.
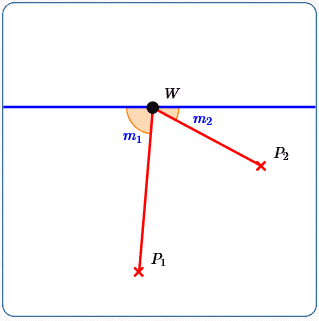
The shortest path from one point ($\,P_1\,$) to the line (at point $\,W\,$) to the second point ($\,P_2\,$) is when the two line segments make equal angles with the line ($\,m_1 = m_2\,$).
Indeed, the following two statements are equivalent:
- $d(P_1,W) + d(P_2,W)\,$ is minimized over all points $\,W\,$ on the line
- $m_1 = m_2\,$
If one statement is true, so is the other. If one statement is false, so is the other.
For ease of reference in what follows,
this equivalence is referred to as the
‘Point/
Proof of the Point/
The Point/Line/Point Equivalence is easy to prove, with a bit of cleverness.
As shown below, reflect $\,\overline{P_2W}\,$ about the line; call the end of the new (reflected) segment $\,P_2'\,.$
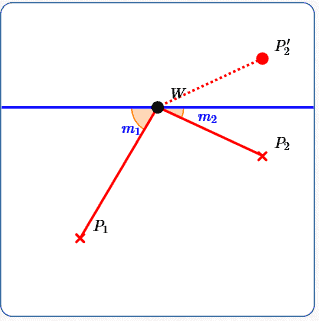
The path from $\,P_1\,$ to $\,W\,$ to $\,P_2\,$ has the same length as the path from $\,P_1\,$ to $\,W\,$ to $\,P_2'\,.$
Now it's clear how to minimize the distance $\,d(P_1,W) + d(P_2,W)\,$: since the shortest distance between two points is a straight line, make a straight-line segment from $\,P_1\,$ to $\,W\,$ to $\,P_2'\,.$
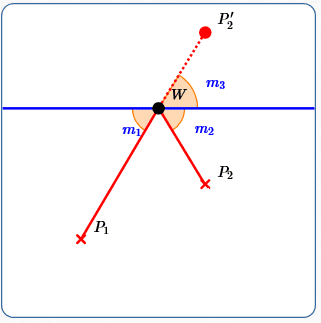
As shown above, let $\,m_3\,$ denote the angle between the ‘wall’ and $\,\overline{P_2'\,W}\,.$
Since vertical angles have equal measures, $\,m_1 = m_3\,.$ As a reflected angle, $\,m_3 = m_2\,.$ Thus, $\,m_1 = m_2\,.$
For the other direction, suppose $\,m_1 = m_2\,.$
Let $\,m_3\,$ denote the reflected angle produced when $\,\overline{P_2W}\,$ is reflected about the ‘wall’. As reflected angles, $\,m_2 = m_3\,.$ Thus, $\,m_1 = m_3\,.$
With $\,m_1 = m_3\,,$ the segment from $\,P_1\,$ to $\,W\,$ to $\,P_2'\,$ is a straight line segment. Thus, $\,d(P_1,W) + d(P_2',W)\,,$ which is equal to $\,d(P_1,W) + d(P_2,W)\,,$ is as small as possible.
Done!