Signs of All the Trigonometric Functions

Sometimes in problem-solving you only need the sign (plus or minus) of a trigonometric value—not its size.

With three already-studied concepts, you have access to the signs of all the trigonometric functions, in all the quadrants:

The unit circle definitions of sine and cosine
The definitions of all the remaining trigonometric functions in terms of sine and cosine
Basic arithmetic facts regarding signs of quotients:

$$\frac{\text{POS}}{\text{NEG}} = \text{NEG}$$

(positive divided by negative is negative)

$$\frac{\text{NEG}}{\text{POS}} = \text{NEG}$$

(negative divided by positive is negative)

$$\frac{\text{NEG}}{\text{NEG}} = \text{POS}$$

(negative divided by negative is positive)

These concepts are reviewed in-a-nutshell here, for your convenience. Need more info? Follow the links given above.

Signs (Plus/Minus) of Sine and Cosine in All Quadrants

By definition, $\,\cos \theta\,$ and $\,\sin\theta\,$ give the $\,x\,$ and $\,y\,$ values (respectively) of points on the unit circle, as shown below.

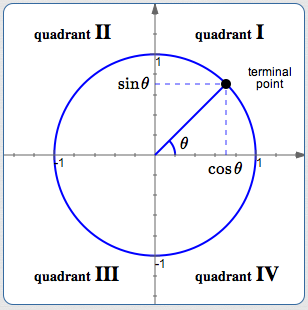
unit circle definitions of sine and cosine

It follows that:

sine is positive in quadrants I and II: points above the $x$-axis have positive $y$-values
sine is negative in quadrants III and IV: points below the $x$-axis have negative $y$-values
cosine is positive in quadrants I and IV: points to the right of the $y$-axis have positive $x$-values
cosine is negative in quadrants II and III: points to the left of the $y$-axis have negative $x$-values

Recall also:

The number zero has no sign: $\,0\,$ is not positive and $\,0\,$ is not negative. Zero is neutral!

For example: $\,\cos \frac{\pi}2 = \cos 90^\circ = 0\,,$ hence has no sign.
If a number is not defined, then (of course) it has no sign.

For example: $\,\tan\frac{\pi}2 = \tan 90^\circ\,$ is not defined, hence has no sign.

Signs (Plus/Minus) of Tangent in All Quadrants

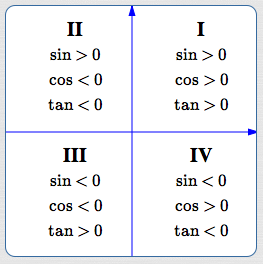
By definition, $\displaystyle\,\tan\theta :=\frac{\sin\theta}{\cos\theta}\,.$ Therefore:

In quadrant I, tangent is positive: $$\cssId{s33}{\frac{POS}{POS} = POS}$$

In quadrant II, tangent is negative: $$\cssId{s35}{\frac{POS}{NEG} = NEG}$$

In quadrant III, tangent is positive: $$\cssId{s37}{\frac{NEG}{NEG} = POS}$$

In quadrant IV, tangent is negative: $$\cssId{s39}{\frac{NEG}{POS} = NEG}$$

Memory Device for the Signs (Plus/Minus) of Sine, Cosine, and Tangent in All Quadrants

memory device for signs of sine, cosine, tangent in all quadrants

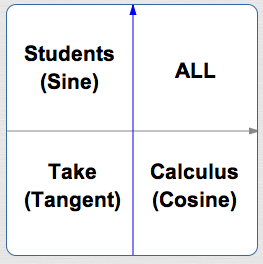
The (optimistic!) memory device

All Students Take Calculus

answers the question:

Where are the (first three) trigonometric functions positive?

They're ALL positive in Quadrant I.
Only the Sine (the ‘S’ in ‘Students’) is positive in Quadrant II.
Only the Tangent (the ‘T’ in ‘Take’) is positive in Quadrant III.
Only the Cosine (the ‘C’ in ‘Calculus’) is positive in Quadrant IV.

Of course, you need to remember to start with the word ‘ALL’ in quadrant I, and then proceed counterclockwise.

This memory device answers the question:

Where are the sine, cosine, and tangent POSITIVE?

Signs (Plus/Minus) of Cotangent, Secant, and Cosecant in All Quadrants

signs of cotangent, secant, and cosecant in all quadrants

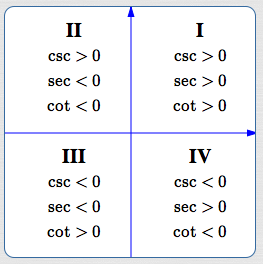
The reciprocal of a number retains the sign of the original number. Therefore, in all the quadrants:

Cosecant has the same sign as sine.
Secant has the same sign as cosine.
Cotangent has the same sign as tangent.