The Trigonometric Functions

Index card: 56ab

Up to now in this Precalculus course, only two trigonometric functions have been studied extensively—sine and cosine. There's a reason for this!

All the remaining trigonometric functions are defined in terms of sine and cosine.

This section discusses the four remaining trigonometric functions: tangent, cotangent, secant, and cosecant.

Definitions: tangent, cotangent, secant, cosecant
A memory device for the six trigonometric functions
Where do the names ‘tangent’ and ‘secant’ come from?
What is the ‘co’ in cosine, cotangent, and cosecant?

Definitions: Tangent, Cotangent, Secant, Cosecant

DEFINITIONS tangent, cotangent, secant, cosecant

Let $\,t\,$ be a real number (restrictions are noted individually below). Think of $\,t\,,$ if desired, as the radian measure of an angle. Then:

$\displaystyle \tan t := \frac{\sin t}{\cos t}$

(‘$\,\tan t\,$’ is formally pronounced ‘tangent of $\,t\,$’)

The tangent function isn't defined where the cosine is zero; this happens at the terminal points $\,(0,1)\,$ and $\,(0,-1)\,.$

Thus, tangent is not defined for $\,t = \frac{k\pi}{2}\,$ for odd integers $\,k\,$: $\,k = \ldots, -5, -3, -1, 1, 3, 5,\, \ldots\,$
$\displaystyle \cot t := \frac{\cos t}{\sin t}$

(‘$\,\cot t\,$’ is formally pronounced ‘cotangent of $\,t\,$’)

The cotangent function isn't defined where the sine is zero; this happens at the terminal points $\,(1,0)\,$ and $\,(-1,0)\,.$

Thus, cotangent is not defined for $\,t = k\pi\,$ for integers $\,k\,$: $\,k = \ldots, -3, -2, -1, 0, 1, 2, 3,\, \ldots\,$
$\displaystyle \sec t := \frac{1}{\cos t}$

(‘$\,\sec t\,$’ is formally pronounced ‘secant (see-cant) of $\,t\,$’)

The secant function has the same restrictions as the tangent.
$\displaystyle \csc t := \frac{1}{\sin t}$

(‘$\,\csc t\,$’ is formally pronounced ‘cosecant of $\,t\,$’)

The cosecant function has the same restrictions as the cotangent.

Notes on the Definitions

Using Function Notation with Trig Functions

The number $\,\tan t\,$ is the output from the tangent function when the input is $\,t\,.$ In other words, ‘$\,\tan\,$’ is the name of the function; $\,t\,$ is the input; $\,\tan t\,$ is the corresponding output.

Recall the convention: for multi-letter function names, parentheses are usually omitted from function notation. That is, $\,\tan(t)\,$ is usually written without parentheses, as $\,\tan t\,,$ when there is no confusion about order of operations.

However, don't ever write something like ‘$\,\tan t + 2\,$’! Clarify as either $\,(\tan t) + 2\,$ (better written as $\,2 + \tan t\,$) or $\,\tan(t+2)\,.$

Similar comments hold for all six trigonometric functions.

Is Cotangent the Reciprocal of the Tangent? Almost!

The cotangent function is almost the reciprocal of the tangent function (but not quite).

So, what's the difference between

$$ \overbrace{\frac{1}{\tan t}}^{\rm reciprocal\ of\ tangent} $$ and $$ \overbrace{\frac{\cos t}{\sin t}}^{\rm definition\ of\ tangent}\ \ \ \ \text{?} $$

First of all, they're equal for all values of $\,t\,$ for which both are defined. However:

$\frac{1}{\tan t}\,$ isn't defined at two types of places: where the tangent isn't defined, and where the tangent is zero.
$\frac{\cos t}{\sin t}\,$ isn't defined at one type of place: where the sine is zero.

For example, $\,\frac{1}{\tan t}\,$ isn't defined at $\,t = \frac{\pi}{2}\,,$ since tangent isn't defined there.

However, $\,\frac{\cos t}{\sin t}\,$ is defined (and equal to zero) at $\,t = \frac{\pi}{2}\,.$

This is a subtle difference, and is usually overlooked in casual discussions. (For example, it is overlooked in the memory device given next.)

Memory Device for the Six Trigonometric Functions

Cosecant is the reciprocal of the sine.

Secant is the reciprocal of the cosine.

Cotangent is the reciprocal of the tangent.

How might you remember these relationships? The memory device below should help!

Write the trig functions vertically, with function followed immediately by cofunction:

sine, cosine, tangent, cotangent, secant, cosecant

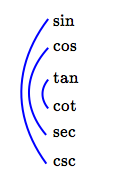
memory device for the six trigonometric functions

Then, connect the functions as shown—they're reciprocals!

Where Do the Names ‘Tangent’ and ‘Secant’ Come From?

Consider an acute angle $\,\theta\,$ laid off in the unit circle. Its terminal point is shown in black below.

Only one auxiliary triangle (in yellow below—it overlaps the green triangle) is needed to explain the significance of the names ‘tangent’ and ‘secant’, as follows:

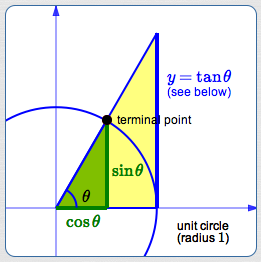
The green and (overlapping) yellow triangles above are similar. Why? They share the angle $\,\theta\,$ and they both have a right angle.

The Word ‘Tangent’

The word ‘tangent’ derives from the Latin tangens, meaning ‘touching’. The tangent gives the length of a segment that is tangent to the unit circle.

	bottom of triangle	right side of triangle
green triangle:	$\cos\theta$	$\sin\theta$
yellow triangle:	$1$	$y$ (initially unknown)

By similarity:

$$ \cssId{s82}{\frac{\sin\theta}{\cos\theta} = \frac{y}{1}} $$

Therefore:

$$ \cssId{s84}{\color{blue}{y = \frac{\sin\theta}{\cos\theta} := \tan\theta}} $$

The Word ‘Secant’

The word ‘secant’ derives from the Latin secare, meaning ‘to cut’. The secant gives the length of a segment that cuts the circle.

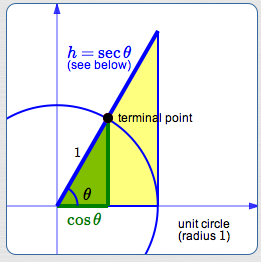
	bottom of triangle	hypotenuse
green triangle:	$\cos\theta$	$1$
yellow triangle:	$1$	$h$ (initially unknown)

By similarity:

$$ \cssId{s94}{\frac{1}{\cos\theta} = \frac{h}{1}} $$

Therefore:

$$ \cssId{s96}{\color{blue}{h = \frac{1}{\cos\theta} := \sec\theta}} $$

What is the ‘co’ in COsine, COtangent, and COsecant?

In English, to complement (not compliment!) is to fill out or to complete.

By definition, the complement of an angle $\,\theta\,$ (given in degree measure) is $\,90^\circ - \theta\,.$ Similarly, the complement of an angle $\,\theta\,$ (given in radian measure) is $\,\frac{\pi}2 - \theta\,.$ Thus, an (acute) angle and its complement, together, fill out a right angle.

The ‘co’ in cosine, cotangent, and cosecant refers to ‘complement’. The following relationships (when they're defined) are true for all real numbers $\,\theta\,$ (not just those in the first quadrant):

cosine is the sine of the complementary angle: $$\cos\theta = \sin(\frac{\pi}2 - \theta)$$
cotangent is the tangent of the complementary angle: $$\cot\theta = \tan(\frac{\pi}2 - \theta)$$
cosecant is the secant of the complementary angle: $$\csc\theta = \sec(\frac{\pi}2 - \theta)$$

Here are sketches/explanations to illustrate these relationships in the first quadrant:

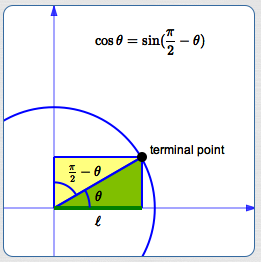
cosine is sine of the complementary angle

By definition:

$$\cssId{s109}{\cos\theta = \ell}$$

Using the right triangle definition:

$$ \displaystyle \cssId{s111}{\sin(\frac{\pi}2 - \theta) = \frac{\text{OPP}}{\text{HYP}} = \frac{\ell}{1} = \ell} $$

Comparing:

$$ \cssId{s113}{\cos\theta = \sin(\frac{\pi}{2} - \theta)} $$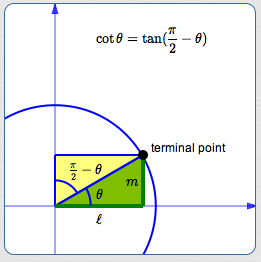

cotangent is tangent of the complementary angle

By definition:

$$ \begin{gather} \cssId{s115}{\cos\theta = \ell}\cr \cssId{s116}{\sin\theta = m}\cr \cssId{s117}{\cot\theta := \frac{\cos\theta}{\sin\theta} = \frac{\ell}{m}} \end{gather} $$

Using the right triangle definition:

$$ \displaystyle \cssId{s119}{\tan(\frac{\pi}2 - \theta) = \frac{\text{OPP}}{\text{ADJ}} = \frac{\ell}{m}} $$

Comparing:

$$ \cssId{s121}{\cot\theta = \tan(\frac{\pi}{2} - \theta)} $$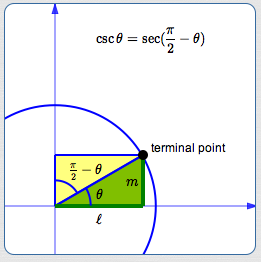

cosecant is secant of the complementary angle

By definition:

$$ \begin{gather} \cssId{s123}{\sin\theta = m}\cr \cssId{s124}{\csc\theta := \frac{1}{\sin\theta} = \frac{1}{m}} \end{gather} $$

Using the definition of secant
and the right triangle definition of cosine:

$$ \begin{align} \sec(\frac{\pi}2 - \theta) &:= \frac{1}{\cos(\frac{\pi}2 - \theta)}\cr &= \frac{1}{m/1}\cr &= \frac{1}{m} \end{align} $$

Comparing:

$$\cssId{s128}{\csc\theta = \sec(\frac{\pi}{2} - \theta)}$$

Here is an excellent reference for historical and cultural information on the trigonometric functions: Dave's Short Trig Course, Clark University