Solving Simple Trigonometric Equations

A trigonometric equation is an equation that uses at least one variable inside a trigonometric function.

Here are some examples of trigonometric equations. Follow the links to see the solutions.

• Example 1:  A single trigonometric function with input $\,x\,,$ no other appearance of the variable: $$\cssId{s6}{\sqrt 2\sin x - 1 = 0}$$
• Example 2:  A single trigonometric function with input $\,kx\,,$ no other appearance of the variable: $$\cssId{s9}{2\cos(3x) = 1}$$
• Example 3 (next section):   A pseudo-quadratic (fake quadratic) trigonometric equation: $$\cssId{s12}{2\sin^2 x - \sin x - 1 = 0}$$
• Example 4:  Use graphical methods to approximate solutions to trigonometric equations:   find all solutions of the equation ‘$\,2\cos x = -3\sin x\,$’ in the interval $\,[0,2\pi]$
• Example 5:  Use WolframAlpha to solve trigonometric equations: $$\cssId{s18}{\tan(5x-3)\sec(x^2 - 7) = 4}$$

Note that an equation like ‘$\,5 - x\sin 3 = 7\,$’ is not a trigonometric equation, because it does not have a variable inside a trigonometric function. Here, $\,\sin 3\,$ is just a constant. This is a linear equation in one variable with unique solution $\,x = \frac{-2}{\sin 3}\,.$

A Single Trigonometric Function With Input $\,x\,,$ No Other Appearance of the Variable

The equation  ‘$\,\sqrt 2\sin x - 1 = 0\,$’  is a trigonometric equation because of the ‘$\,x\,$’ inside the sine function. Note that there is no other appearance of $\,x\,$ in this equation.

In cases such as this, we start by isolating the trigonometric function containing the variable. (Recall that isolate means to get all by itself on one side of the equation.)

Solution

Isolate the trigonometric function with variable input:

• Add $\,1\,$ to both sides (using the addition property of equality)
• Divide both sides by $\,\sqrt 2\,$ (using the multiplication property of equality)

At this point, several ‘checks’ should run through your head:

Is the equation ever true? Can an output from the sine function ever equal $\,\frac{1}{\sqrt 2}\,$?

The range of the sine function is $\,[-1,1]\,.$ Since $\,\sqrt 2 \approx 1.4 \gt 1\,,$ we have $\,\frac{1}{\sqrt 2} \approx 0.7 \lt 1 \,.$ So, the number $\,\frac{1}{\sqrt 2}\,$ is in the range of the sine function. Thus, there is at least one value for which the equation is true.

How many solutions does the equation have?

A quick sketch (below) shows that there are infinitely many solutions. This is typical of trigonometric equations—they often have infinitely many solutions, because of the periodic nature of trigonometric functions.

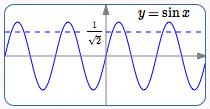
Punchline: All the Solutions for Example 1

Reporting the solutions in degrees:

• $x = 45^\circ + {360k\,}^\circ\,$ for all integers $\,k\,,$ or
• $x = 135^\circ + {360k\,}^\circ\,$ for all integers $\,k$

Reporting the solutions in radians:

• $\displaystyle x = \frac{\pi}{4} + 2\pi k\,$ for all integers $\,k\,,$ or
• $\displaystyle x = \frac{3\pi}{4} + 2\pi k\,$ for all integers $\,k$

Here's Where These Solutions Come From

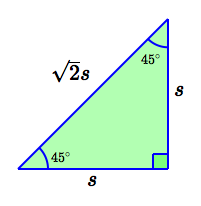
Precisely what angles have sine equal to $\,\frac{1}{\sqrt 2}\,$? From the special triangle below, we see that $\,\sin 45^\circ = \frac{1}{\sqrt 2}\,$; so, $\,45^\circ\,$ (or $\,\frac{\pi}{4}\,$ radians) is one of the solutions of the equation.

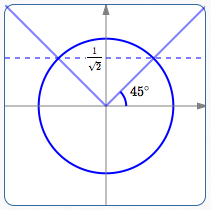
Recall that the sine function gives the $y$-values of points on the unit circle. From the unit circle above, we can now get all the angles with $y$-value equal to $\,\frac{1}{\sqrt 2}\,,$ as follows:

Recall that, when laying off angles:

Counterclockwise is the positive direction and clockwise is the negative direction

Also recall that the integers are:

Start at the terminal point for $\,45^\circ\,,$ in the first quadrant:

See the pattern? Together, these give all the solutions in the first quadrant:

Next, start at the terminal point for $\,180^\circ - 45^\circ = 135^\circ\,,$ in the second quadrant:

See the same pattern? Together, these give all the solutions in the second quadrant:

Example 2

A Single Trigonometric Function With Input $\,kx\,,$ No Other Appearance of the Variable

The equation ‘$\,2\cos(3x) = 1\,$’ is a trigonometric equation because of the ‘$\,x\,$’ inside the cosine function. Note that there is no other appearance of $\,x\,$ in this equation.

Solution

Again, we start by isolating the trigonometric function containing the variable.

Isolate the trigonometric function with variable input. The cosine function takes on the value $\,\frac 12\,$ infinitely many times, so again there are infinitely many solutions.

Punchline: All the ‘Pre’-Solutions for Example 2

To get $\,x\,$ in degrees:

• $3x = 60^\circ + {360k\,}^\circ\,$ for all integers $\,k\,,$ or
• $3x = -60^\circ + {360k\,}^\circ\,$ for all integers $\,k$

To get $\,x\,$ in radians:

• $\displaystyle 3x = \frac{\pi}{3} + 2\pi k\,$ for all integers $\,k\,,$ or
• $\displaystyle 3x = -\frac{\pi}{3} + 2\pi k\,$ for all integers $\,k$

Here's Where These ‘Pre’-Solutions Come From

For the moment, ignore the ‘$\,3x\,$’ inside the cosine function. (We'll use it in a minute.)

Ask:  What angles have cosine equal to $\,\frac{1}{2}\,$?

From the special triangle below, we see that $\,\cos 60^\circ = \frac{1}{2}\,.$

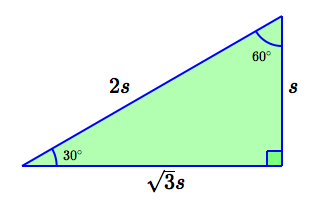
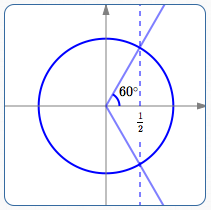
Recall that the cosine function gives the $x$-values of points on the unit circle.

As in Example 1, get all the angles with $x$-value equal to $\,\frac{1}{2}\,$:

$60^\circ + {360k\,}^\circ\,$ for all integers $\,k\,$ (in quadrant I)   (*)

$-60^\circ + {360k\,}^\circ\,$ for all integers $\,k\,$ (in quadrant IV)   (**)

These are all possible angles with cosine equal to $\,\frac 12\,.$

Now, we'll use the ‘$\,3x\,$’.

Note that if $\,x\,$ has units of degrees, then $\,3x\,$ also has units of degrees.

The angle inside the cosine function (which in this example is $\,3x\,$) must equal one of the angles in (*) or (**), in order to have cosine equal to $\,\frac 12\,.$

Thus, for all integers $\,k\,,$ and for $\,x\,$ in degrees:

Solve for $\,x\,$ (by dividing both sides of the equations by $\,3\,$):

Degree measure:

$\displaystyle x = \frac{60^\circ + {360k\ }^\circ}{3} = 20^\circ + {120k\,}^\circ\,$ for all integers $\,k$

or

$\displaystyle x = \frac{-60^\circ + {360k\ }^\circ}{3} = -20^\circ + {120k\,}^\circ\,$ for all integers $\,k$

Radian measure:

$\displaystyle x = \frac{\frac\pi 3 + 2\pi k}{3} = \frac{\pi}{9} + \frac{2\pi k}{3}\,$ for all integers $\,k$

or

$\displaystyle x = \frac{-\frac\pi 3 + 2\pi k}{3} = -\frac{\pi}{9} + \frac{2\pi k}{3}\,$ for all integers $\,k\,$

  Done!

Example 3 (next section)

Example 4

Use Graphical Methods To Approximate Solutions To Trigonometric Equations

Graphical methods for solving equations (and inequalities) were studied thoroughly in earlier sections:

• Graphical Interpretations of Sentences like $\,f(x) = 0\,$ and $\,f(x) \gt 0$
• Graphical Interpretations of Sentences like $\,f(x) = g(x)\,$ and $\,f(x) \gt g(x)$

Even if you're working with a simple equation (as in Examples 1 and 2), graphical methods are great for giving yourself confidence in your answers and/or catching mistakes. Graphical methods typically provide approximate solutions, not exact solutions.

The equation ‘$\,2\cos x = -3\sin x\,$’ is a trigonometric equation because there is at least one variable inside a trigonometric function.

In this equation, there are two trigonometric functions with variable inputs. Isolating either one would still cause a variable expression (not a constant) to appear on the other side of the equation. Thus, the technique illustrated in Example 1 and Example 2 doesn't work.

Both sides of the equation ‘$\,2\cos x = -3\sin x\,$’ are easy to graph—it is well-suited to graphical methods. Graph the left-hand side; graph the right-hand side; approximate the intersection point(s) in a desired interval.

Solution

original equation;
find solutions in the interval $\,[0,2\pi]$

Punchline: Solutions for Example 4

$x\approx 2.6\,$  or  $\,x\approx 5.7$

Here's Where These Solutions Come From

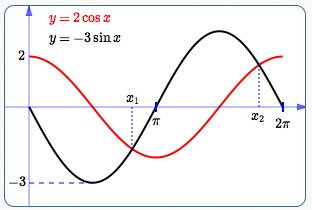
Graph, on the interval $\,[0,2\pi]\,$:

• The left-hand side of the equation (in red): cosine curve, vertical stretch by a factor of $\,2$
• The right-hand side of the equation (in black): sine curve, vertical stretch by a factor of $\,3\,,$ reflect about the $x$-axis

It is clear there are exactly two solutions in the interval $\,[0,2\pi]\,$; these correspond to the intersection points of the two graphs:

• $x_1\,$ is a bit less than $\,\pi\,$:  $\color{red}{2\cos x_1} \approx -3\sin x_1$
• $x_2\,$ is a bit less than $\,2\pi\,$:  $\color{red}{2\cos x_2} \approx -3\sin x_2$

A graphing calculator or WolframAlpha (see Example 5) can be used to get decimal approximations for $\,x_1\,$ and $\,x_2\,.$

Example 5

Use WolframAlpha to Solve Trigonometric Equations

WolframAlpha (opens in a new window) is a powerful, reliable, and free resource for mathematical information. WolframAlpha understands conventional math syntax and abbreviations. You can also type in a reasonable guess, and WolframAlpha will try to make sense of it.

For example, if you type in  ‘sine of x’  and press Enter, the  ‘Input’  area will display ‘$\,\sin(x)\,$’. This lets you know that WolframAlpha has understood you correctly. Always check the  ‘Input’  area, to make sure that you and WolframAlpha are on the same page!

Try solving each of the examples from this page (or the exercises) at WolframAlpha. WolframAlpha is a good resource for checking answers, gaining additional insight, or when you just need a quick reliable answer.

You can cut-and-paste each of the following. Have fun!

tan(5x-3)sec(x^2 - 7) = 4

sin(x) = 1/sqrt(2)

2cos(3x) = 1

2sin^2 x - sin x - 1 = 0

2cos(x) = -3sin(x), 0 <= x <= 2pi

WolframAlpha gives exact solutions when possible; click ‘Approximate forms’ if desired.