The Multiplication Property of Equality

In the previous section, we learned that adding/subtracting
the same number to/from both sides of an equation
makes the equation look different, but doesn't change its truth.
This tool is used to ‘transform’ an equation into (an equivalent) one that is easier to work with.

A second transforming tool, the Multiplication Property of Equality,
is the subject of this section, and is stated below:

THEOREM the Multiplication Property of Equality

For all real numbers

$\,a\,$ and

$\,b\,$, and for

$\,c \ne 0\,$:

$$ a = b \ \ \text{⇔}\ \ ac = bc $$

Note: Here's how to read aloud that sentence:

$a = b$	$\text{⇔}$	$ac = bc$
$a$ equals $b$	is equivalent to	$ac$ equals $bc$

To a person not trained in reading mathematics, the information contained in this theorem is completely inaccessible.
If you don't understand the language in which an idea is being expressed, then you can't use the idea.

So, what is this theorem telling us that we can do?

To answer this question, you need to ask yourself:
What did you do to ‘$a = b\,$’ to transform it into ‘$ac = bc\,$’ ?
ANSWER: You multiplied both sides by $\,c\,$.

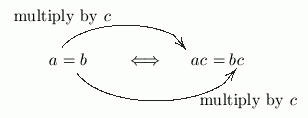
Hence the first part of the translation:

You can multiply both sides of an equation by the same nonzero number,
and this won't change the truth of the equation.

Continuing the translation:
What did you do to ‘$ac = bc\,$’ to transform it to ‘$a = b\,$’ ?
ANSWER: You divided both sides by $\,c\,$.

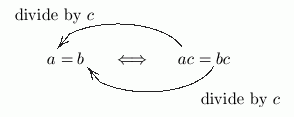
Hence the rest of the translation:

You can divide both sides of an equation by the same nonzero number,
and this won't change the truth of the equation.

So, here's the full translation of the Multiplication Property of Equality:
this is the way a math teacher might translate the Multiplication Property of Equality,
to tell students what they can do:

You can multiply (or divide) both sides of an equation by the same nonzero number,
and this won't change the truth of the equation.

What goes wrong with multiplying or dividing by zero?
That is, why isn't $\,c\,$ allowed to equal zero in the Multiplication Property of Equality?

First of all, recall that division by zero is undefined; it's nonsensical; it's just not allowed.
So zero certainly needs to be excluded when dividing.

But what about multiplying by zero?
The problem is that multiplying by zero can change the truth of an equation:
it can take a false equation to a true equation.
To see this, consider the false equation ‘$\,2 = 3\,$’ .
Multiplying both sides by zero results in the new equation ‘$\,2\cdot 0 = 3\cdot 0\,$’ (that is, ‘$\,0 = 0\,$’), which is true.

Multiplying by zero can take a false equation to a true equation:

$2 = 3$	FALSE
$2\cdot 0 = 3\cdot 0$	multiply both sides by $0$
$0 = 0$	TRUE

Here, you will practice recognizing equivalent equations.
Also, you will identify what you are doing to one equation to get an equivalent equation.

EXAMPLES:

Question:
Equation #1:

$x = 5$
Equation #2:

$2x = 10$
Are these equations equivalent?
If YES, then what did you DO to Equation #1 to get Equation #2?

Solution:
YES; multiply both sides by 2

Question:
Equation #1:

$x - 1 = 3$
Equation #2:

$-x + 1 = -3$
Are these equations equivalent?
If YES, then what did you DO to Equation #1 to get Equation #2?

Solution:
YES; multiply both sides by $-1$

Question:
Equation #1:

$x + 2 = 5$
Equation #2:

$3x + 6 = 15$
Are these equations equivalent?
If YES, then what did you DO to Equation #2 to get Equation #1?

Solution:
YES; divide both sides by $3$

Question:
Equation #1:

$2x = 5$
Equation #2:

$6x = 8$
Are these equations equivalent?
If YES, then what did you DO to Equation #1 to get Equation #2?

Solution:
NOT EQUIVALENT

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Solving Simple Linear Equations with Integer Coefficients