 Horizontal and Vertical Stretching/Shrinking
Horizontal and Vertical Stretching/Shrinking
|
|
|
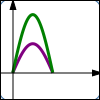
$y = f(x)$ $y = 2f(x)\,$ Vertical stretch; $y$-values are doubled; points get farther away from $x$-axis |
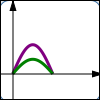
$y = f(x)$ $y = \frac{f(x)}{2}\,$ Vertical shrink; $y$-values are halved; points get closer to $x$-axis |
|
Vertical stretching/shrinking changes the $y$-values of points. Transformations that affect the $y$-values are intuitive. |
|
|
|
|
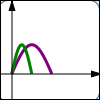
$y = f(x)$ $y = f(2x)\,$ Horizontal shrink; $x$-values are halved; points get closer to $y$-axis |
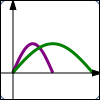
$y = f(x)$ $y = f(\frac x2)$ Horizontal stretch; $x$-values are doubled; points get farther away from $y$-axis |
|
Horizontal stretching/shrinking changes the $x$-values of points. Transformations that affect the $x$-values are counter-intuitive. |
|
The lesson Graphing Tools: Vertical and Horizontal Scaling in the Algebra II curriculum gives a thorough discussion of horizontal and vertical stretching and shrinking. The key concepts are repeated here.
The exercises in this lesson duplicate those in Graphing Tools: Vertical and Horizontal Scaling .
Ideas Regarding Vertical Scaling (Stretching/Shrinking)
-
Points on the graph of $\,y=f(x)\,$ are of the form $\,\bigl(x,f(x)\bigr)\,.$
Points on the graph of $\,y=3f(x)\,$ are of the form $\,\bigl(x,3f(x)\bigr)\,.$
Thus, the graph of $\,y=3f(x)\,$ is found by taking the graph of $\,y=f(x)\,,$ and multiplying the $y$-values by $\,3\,.$ This moves the points farther from the $x$-axis, which tends to make the graph steeper.
-
Points on the graph of $\,y=f(x)\,$ are of the form $\,\bigl(x,f(x)\bigr)\,.$
Points on the graph of $\,y=\frac13f(x)\,$ are of the form $\,\bigl(x,\frac13f(x)\bigr)\,.$
Thus, the graph of $\,y=\frac13f(x)\,$ is found by taking the graph of $\,y=f(x)\,,$ and multiplying the $y$-values by $\,\frac13\,.$ This moves the points closer to the $x$-axis, which tends to make the graph flatter.
- Transformations involving $\,y\,$ work the way you would expect them to work—they are intuitive.
-
Here is the thought process you should use when you are given the graph of $\,y=f(x)\,$ and asked about the graph of $\,y=3f(x)\,$:
Interpretation of new equation:
$$ \begin{gather} \overset{\text{the new y-values}}{\overbrace{ \strut\ \ y\ \ }} \overset{\text{are}}{\overbrace{ \strut\ \ =\ \ }} \overset{\text{three times}\ \ }{\overbrace{ \strut \ \ 3\ \ }} \overset{\text{the previous y-values}}{\overbrace{ \strut\ \ f(x)\ \ }} \end{gather} $$Summary of Vertical Scaling
Let $\,k \gt 1\,.$ Start with the equation $\,y=f(x)\,.$ Multiply the previous $y$-values by $\,k\,,$ giving the new equation $\,y=kf(x)\,.$ The $y$-values are being multiplied by a number greater than $\,1\,,$ so they move farther from the $x$-axis. This tends to make the graph steeper, and is called a vertical stretch.
Let $\,0 \lt k \lt 1\,.$ Start with the equation $\,y=f(x)\,.$ Multiply the previous $y$-values by $\,k\,,$ giving the new equation $\,y=kf(x)\,.$ The $y$-values are being multiplied by a number between $\,0\,$ and $\,1\,,$ so they move closer to the $x$-axis. This tends to make the graph flatter, and is called a vertical shrink.
In both cases, a point $\,(a,b)\,$ on the graph of $\,y=f(x)\,$ moves to a point $\,(a,kb)\,$ on the graph of $\,y=kf(x)\,.$
This transformation type is formally called vertical scaling (stretching/shrinking).
Ideas Regarding Horizontal Scaling (Stretching/Shrinking)
-
Points on the graph of $\,y=f(x)\,$ are of the form $\,\bigl(x,f(x)\bigr)\,.$
Points on the graph of $\,y=f(3x)\,$ are of the form $\,\bigl(x,f(3x)\bigr)\,.$
-
How can we locate these desired points $\,\bigl(x,f(3x)\bigr)\,$?
First, go to the point $\,\color{red}{\bigl(3x\,,\,f(3x)\bigr)}\,$ on the graph of $\,\color{red}{y=f(x)}\,.$
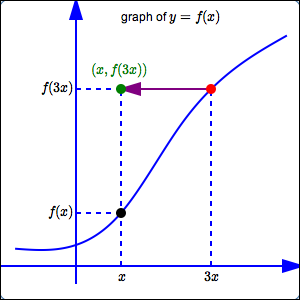
This point has the $y$-value that we want, but it has the wrong $x$-value. The $x$-value of this point is $\,3x\,,$ but the desired $x$-value is just $\,x\,.$
Thus, the current $\color{purple}{x}$-value must be divided by $\,\color{purple}{3}\,$. The $\color{purple}{y}$-value remains the same. This gives the desired point $\,\color{green}{\bigl(x,f(3x)\bigr)}\,.$
Thus, the graph of $\,y=f(3x)\,$ is the same as the graph of $\,y=f(x)\,,$ except that the $x$-values have been divided by $\,3\,$ (not multiplied by $\,3\,,$ which you might expect).
Notice that dividing the $x$-values by $\,3\,$ moves them closer to the $y$-axis. This is called a horizontal shrink.
-
Transformations involving $\,x\,$ do NOT work the way you would expect them to work! They are counter-intuitive—they are against your intuition.
-
Here is the thought process you should use when you are given the graph of $\,y=f(x)\,$ and asked about the graph of $\,y=f(3x)\,$:
$$ \begin{align} \text{original equation:} &\quad y=f(x)\cr \text{new equation:} &\quad y=f(3x) \end{align} $$$$ \begin{gather} \text{Interpretation of new equation:}\cr\cr y = f( \overset{\text{replace $x$ by $3x$}}{\overbrace{ \ \ 3x\ \ }} ) \end{gather} $$Replacing every $\,x\,$ by $\,3x\,$ in an equation causes the $x$-values in the graph to be DIVIDED by $\,3\,.$
Summary of Horizontal Scaling
Let $\,k\gt 1\,.$ Start with the equation $\,y=f(x)\,.$ Replace every $\,x\,$ by $\,kx\,$ to give the new equation $\,y=f(kx)\,.$ This causes the $x$-values on the graph to be DIVIDED by $\,k\,,$ which moves the points closer to the $y$-axis. This is called a horizontal shrink. A point $\,(a,b)\,$ on the graph of $\,y=f(x)\,$ moves to a point $\,(\frac{a}{k},b)\,$ on the graph of $\,y=f(kx)\,.$
Additionally:
Let $\,k\gt 1\,.$ Start with the equation $\,y=f(x)\,.$ Replace every $\,x\,$ by $\,\frac{x}{k}\,$ to give the new equation $\,y=f(\frac{x}{k})\,.$ This causes the $x$-values on the graph to be MULTIPLIED by $\,k\,,$ which moves the points farther away from the $y$-axis. This is called a horizontal stretch. A point $\,(a,b)\,$ on the graph of $\,y=f(x)\,$ moves to a point $\,(ka,b)\,$ on the graph of $\,y=f(\frac{x}{k})\,.$
This transformation type is formally called horizontal scaling (stretching/shrinking).
Different Words Used to Talk About Transformations Involving $\,y\,$ and $\,x\,$
Notice that different words are used when talking about transformations involving $\,y\,,$ and transformations involving $\,x\,.$
For transformations involving $\,y\,$ (that is, transformations that change the $y$-values of the points), we say:
DO THIS to the previous $y$-value
For transformations involving $\,x\,$ (that is, transformations that change the $x$-values of the points), we say:
REPLACE the previous $x$-values by $\ldots$
Make Sure You See the Difference!
Vertical scaling:
Going from
$\,y=f(x)\,$
to
$\,y = kf(x)\,$ for $\,k\gt 0$
Horizontal scaling:
Going from
$\,y = f(x)\,$
to
$\,y = f(kx)\,$ for $\,k\gt 0$
Make sure you see the difference between (say) $\,y = 3f(x)\,$ and $\,y = f(3x)\,$!
In the case of $\,y = 3f(x)\,,$ the $\,3\,$ is ‘on the outside’: we're dropping $\,x\,$ in the $\,f\,$ box, getting the corresponding output, and then multiplying by $\,3\,.$ This is a vertical stretch.
In the case of $\,y = f(3x)\,,$ the $\,3\,$ is ‘on the inside’: we're multiplying $\,x\,$ by $\,3\,$ before dropping it into the $\,f\,$ box. This is a horizontal shrink.