Solving Polynomial Equations

There are different situations where you may need to solve a polynomial equation:

1. In a classroom, to demonstrate that you have learned appropriate solution techniques.
2. Outside of a classroom (in a real-life application!) where you only need to get the solutions—you don't need to know how they were found.

In the second situation, jump up to https://www.wolframalpha.com and type in something like this:

solve x^5 - 2 = 2x^3 + 2x^2 + 3x

Try it! You'll be presented with all the complex solutions (which of course include the real solutions), together with appropriate graphs. Easy, quick, reliable, and free.

If you find yourself in the classroom situation, then this lesson is for you—and it will also be a great review, pulling together ideas from prior sections.

Solutions of Polynomial Equations: General Concepts

All polynomials in this lesson are assumed to have real number coefficients.

Therefore, instead of saying things like

‘Let $\,P(x) = ax + b\,$ where $\,a\,$ and $\,b\,$ are real numbers and $\,a\ne 0\,$’

we can more simply say:

‘Let $\,P(x) = ax + b\,,$ where $\,a\ne 0\,$’

Polynomial Equations of Degree $\,1$

Polynomial equations of degree $\,1\,$ are called linear equations. The standard form is $\,ax + b = 0\,,$ for $\,a\ne 0\,.$

They are solved using the addition and multiplication properties of equality.

The unique solution is $\,x = -\frac{b}{a}\,.$

Polynomial Equations of Degree $\,2$

Polynomial equations of degree $\,2\,$ are called quadratic equations. The standard form is $\,ax^2 + bx + c = 0\,,$ for $\,a\ne 0\,.$

They are solved using the quadratic formula.

The solutions are:

The discriminant is: $$b^2 - 4ac$$

If the discriminant is positive, there are two different real number solutions—call them $\,r_1\,$ and $\,r_2\,.$

In this case: $$ax^2 + bx + c = a(x - r_1)(x - r_2)$$

If the discriminant is zero, there is exactly one real number solution—call it $\,r\,.$

In this case: $$ax^2 + bx + c = a(x - r)^2$$

If the discriminant is negative, there are no real number solutions. Instead, there is a complex conjugate pair of solutions, call them $\,z_1\,$ and $\,z_2\,.$

In this case, $ax^2 + bx + c\,$ is irreducible—it can't be factored using real numbers.

However, it can be factored using the complex conjugate pair: $$ax^2 + bx + c = a(x - z_1)(x - z_2)$$

Polynomial Equations of Degrees $\,3\,$ and $\,4$

Polynomial equations of degree $\,3\,$ are called cubic equations.

Polynomial equations of degree $\,4\,$ are called quartic equations.

There do exist methods for finding exact solutions of cubic and quartic equations. However, these methods are hard to use, and they usually give big, complicated radical expressions for the solutions.

Cubic and quartic equations that you run into in math classes usually tend to be a bit contrived and can be solved using the method discussed in this lesson.

Polynomial Equations of Degrees $\,5\,$ and Above

For polynomial equations of degree $5$ and above, there are no general solution methods. That is, there are no methods that will always give all the exact solutions.

Again, however, the ones that you run into in math classes can usually be solved by using the method discussed in this lesson.

Polynomial Equations of Degrees $\,n$

Every polynomial equation of degree $\,n\,$ (where $\,n = 1,2,3,...\,$) with real number coefficients has exactly $\,n\,$ solutions in the set of complex numbers, counting multiplicities.

Any non-real solutions must occur in complex conjugate pairs.

For example, the fifth degree polynomial equation ‘$\,(x-2)^5 = 0\,$’ has exactly one real number solution, $\,x = 2\,,$ which has multiplicity $\,5\,.$

Here's a second example. The polynomial equation ‘$\,8(x-1)^2x^3(x^2 + 1) = 0\,$’ has degree $\,7\,.$ It has two real solutions: $\,1\,$ and $\,0\,.$ Setting the irreducible quadratic $\,x^2 + 1\,$ equal to zero gives two non-real solutions—the complex conjugate pair $\,i\,$ and $\,-i\,.$

• The real solution $\,1\,$ has multiplicity $\,\color{red}{2}\,,$ from the $\,(x-1)^{\color{red}{2}}\,.$
• The real solution $\,0\,$ has multiplicity $\,\color{red}{3}\,,$ from the $\,x^{\color{red}{3}}\,.$
• The solution $\,i\,$ has multiplicity $\,\color{red}{1}\,.$
• The solution $\,-i\,$ has multiplicity $\,\color{red}{1}\,.$

Note that $\,\color{red}{2} + \color{red}{3} + \color{red}{1} + \color{red}{1} = 7\,.$ In factored form over the set of complex numbers, the equation is written as ‘$\,8(x-1)^2(x^3)(x-i)(x+i) = 0\,$’.

An Approach for Finding Exact Solutions of (Some) Polynomial Equations of Degree $\,3^+$

General Procedure

(white background)

Example

(light blue background)

Solve the equation: $$\cssId{s67}{x^5 - 2 = 2x^3 + 2x^2 + 3x}$$

STEP 1:

Write the equation in the form $\,P(x) = 0\,.$ That is, get the number zero on the right-hand side; the polynomial on the left is asigned the named $\,P(x)\,.$

The zeros of $\,P\,$ are the solutions of the equation.

Subtract $\,2x^3 + 2x^2 + 3x\,$ from both sides to get this equivalent equation:

$$ \cssId{s74}{\underbrace{x^5 - 2x^3 - 2x^2 - 3x - 2}_{P(x)} = 0} $$

STEP 2:

Use the Bounding the Real Roots of a Polynomial theorem to get a bound on the real zeros of $\,P\,.$ Call this bound $\,K\,.$

Use a graphing device (such as a graphing calculator or the WolframAlpha widget supplied below) to graph $\,P\,$ using the initial window $\,-10\le y\le 10\,$ and $\,-K\le x\le K\,.$

You're looking for a ‘nice’ zero—preferably an integer. Use the behavior of the graph to guess the multiplicity of each zero. Find all ‘nice’ zeros, re-graphing on tighter intervals as needed.

$$ \begin{align} &\cssId{s84}{K}\cr &\ \cssId{s85}{= 1 + \frac{\text{max of absolute values of coefficients}}{\text{absolute value of leading coefficient}}}\cr &\ \cssId{s86}{= 1 + \frac{3}{1} = 4} \end{align} $$

From the graph below (obtained using the WolframAlpha widget), it's clear that there are only two real zeros: $\,-1\,$ and $\,2\,.$

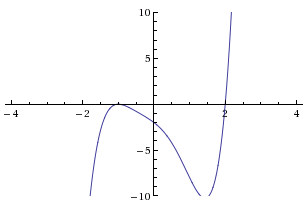
The number $\,2\,$ is clearly a simple zero. The number $\,-1\,$ probably has multiplicity two.

STEP 3:

Check your (potential) zeros from Step 2. You don't want to think that (say) $\,2\,$ is a zero, when it's actually $\,1.9\,$!

Use synthetic division and the Remainder Theorem to do the checks.

Don't forget the $\,0\,$ from the missing $\,x^4\,$ term in $\,P(x)\,$!

$2$	$1$	$0$	$-2$	$-2$	$-3$	$-2$
		$2$	$4$	$4$	$4$	$2$
$-1$	$1$	$2$	$2$	$2$	$1$	$0$	$\leftarrow$ so $2$ is a zero
		$-1$	$-1$	$-1$	$-1$
$-1$	$1$	$1$	$1$	$1$	$0$		$\leftarrow$ so $-1$ is a zero
		$-1$	$0$	$-1$
	$\color{green}{1}$	$\color{green}{0}$	$\color{green}{1}$	$0$			$\leftarrow$ so $-1$ is a zero again

STEP 4:

Use the bottom row of the synthetic division to get the factor that remains after all factors corresponding to real zeros have been divided out.

The $\ \ \color{green}{1}\ \ \ \color{green}{0}\ \ \ \color{green}{1}\ \ $ from the last row of the synthetic division represents: $$1x^2 + 0x + 1 = x^2 + 1$$

Thus, we have:

$$ \cssId{s101}{\frac{P(x)}{(x-2)(x+1)(x+1)} = x^2 + 1} $$

Or, equivalently:

$$ \begin{align} &x^5 - 2x^3 - 2x^2 - 3x - 2\cr &\quad = (x-2)(x+1)^2(x^2 + 1) \end{align} $$

STEP 5:

Set the last factor (if any) equal to zero, and solve if possible.

$$ \begin{gather} \cssId{s106}{x^2 + 1 = 0}\cr \cssId{s107}{x^2 = -1}\cr \cssId{s108}{x = \pm\sqrt{-1}}\cr \cssId{s109}{x = \pm i} \end{gather} $$

STEP 6:

Use the results from Step 5 to factor $\,P(x)\,$ as completely as possible.

$$\cssId{s112}{P(x) = (x-2)(x+1)^2(x - i)(x + i)}\,$$

STEP 7:

State the solutions to the original equation.

The solutions of the original equation (where repetition indicates multiplicity) are:

$-1\,,$   $-1\,,$   $2\,,$   $i\,,$   and   $-i$