Shifting Conics
(Shifting any Equation in Two Variables)

LESSON READ-THROUGH
by Dr. Carol JVF Burns (website creator)
Follow along with the highlighted text while you listen!
Thanks for your support!
 

The equations of conic sections have been thoroughly explored in prior sections.
However, these conics were all conveniently ‘centered’ at the origin (giving the so-called ‘standard forms’):

By introducing just one new simple idea, any conic section (indeed, the graph of any equation in two variables)
can be shifted up/down/left/right to any desired place in the coordinate plane.

A General Representation for Equations in Two Variables

Recall from Introduction to Equations and Inequalities in Two Variables that
an equation in two variables requires substitution of two variables to determine its truth (true or false).

The graph of an equation in two variables ($\,x\,$ and $\,y\,$) is a picture of its solution set;
it is the set of all points $\,(x,y)\,$ that make the equation true.

Every equation in two variables can be expressed in the form $\,F(x,y) = 0\,.$
Here, $\,F\,$ is a function of two variables—it takes two inputs, and gives a unique corresponding output.
To put an equation in this form, just re-arrange the equation to put all the terms on the left, thus getting $\,0\,$ on the right.
Then, use the resulting left side to define the function $\,F\,.$

For example, consider the equation $\,y^2 = 2xy\,.$
First, rewrite as the equivalent equation $\,y^2 - 2xy = 0\,.$
Then, define $\,F(x,y) := y^2 - 2xy\,.$
The equation is now of the form $\,F(x,y) = 0\,$!

In particular, note that every conic section (parabolas, ellipses, hyperbolas) can be put in the form $\,F(x,y) = 0\,.$

$\,y = f(x)\,$ is a Special Case of $\,F(x,y) = 0\,$

You've been working with a special case of $\,F(x,y) = 0\,$ for years now!
For some equations (but not all), you can get an equivalent equation with $\,y\,$ all by itself on one side, and all the $\,x\,$ stuff on the other side.
If you can do this, then the equation is of the (very familiar) form $\,y = f(x)\,.$

In the $\,y = f(x)\,$ situation, every $\,x\,$ has a unique corresponding $\,y\,$ that makes the equation true.
Therefore, the graph of every equation of the form $\,y = f(x)\,$ passes the vertical line test.
Oh, so many familiar examples: $\,y = mx + b\,,$   $\,y = ax^2 + bx + c\,,$   $\displaystyle\,y = \sqrt{x}\,,$   $\displaystyle\,y = \frac{5x-1}{\root 3\of{1 - x^2}}\,,$   and on and on.

Note:
If a graph doesn't pass the vertical line test, then it doesn't have an equation of the form $\,y = f(x)\,.$

For equations of the form $\,y = f(x)\,,$ it's easier/more natural/more conventional to treat graphical transformations differently,
depending on whether you're working with $\,x\,$ or with $\,y\,.$ If needed, review this earlier section for the different words used:

Transformations Involving $\,y\,$ for Equations that are not of the Form $\,y = f(x)\,$

When the appearance of $\,y\,$ in an equation gets more complicated, we need to switch gears:

To apply graphical transformations to any equation in $\,x\,$ and $\,y\,,$
(no matter how mixed-up the variables might be),
just use the ‘replace every...’ language for both $\,x\,$ and $\,y\,.$

Then, both cases are counter-intuitive!

For example, consider the circle $\,x^2 + y^2 = 5\,.$
Want to shift it LEFT four units? Replace every $\,x\,$ by $\,x \color{red}{+} 4\,.$
Want to shift it UP three units? Replace every $\,y\,$ by $\,y \color{red}{-} 3\,.$
The new equation is: $\,(x+4)^2 + (y - 3)^2 = 5\,.$
Both counter-intuitive! Both against your intuition!

Why Does This Work?

It's easy to see why this works for any equation of the form $\,F(x,y) = 0\,,$ as follows:

Read through this several times (as needed) to make sure you get it.
It's a simple idea, but a bit symbol-intensive—which makes it look harder than it really is.

Summary: Shifting any Equation in Two Variables Up/Down/Left/Right

Let $\,k > 0\,,$ and consider any equation in two variables ($\,x\,$ and $\,y\,$).

Replacing every$\,x\,$by$\,x+k\,$shifts the graphLEFT$\,k\,$units.
Replacing every$\,x\,$by$\,x-k\,$shifts the graphRIGHT$\,k\,$units.
Replacing every$\,y\,$by$\,y+k\,$shifts the graphDOWN$\,k\,$units.
Replacing every$\,y\,$by$\,y-k\,$shifts the graphUP$\,k\,$units.

A Final Note: Applying the New Approach to the $\,y = f(x)\,$ Situation

If you really want, you can apply the ‘new’ approach to the ‘$\,y = f(x)\,$’ situation.
(However, I think it's like killing a mosquito with a sledgehammer!)

Here's an example:
Want to shift $\,y = x^2\,$ UP four units?
Then, replace every $\,y\,$ with $\,y \color{red}{-} 4\,.$
This gives the new equation $\,y - 4 = x^2\,.$
Of course, this is equivalent to $\,y = x^2 + 4\,$!

Have Fun Shifting Equations in Two Variables at WolframAlpha

Just for fun, zip up to WolframAlpha.
Type in any equation in two variables. (Try to stump it!)
Put a comma after this first equation.
Then, type in the same equation, except with every $\,x\,$ replaced by (say) $\,x + 4\,,$ and every $\,y\,$ replaced by (say) $\,y - 7\,.$
What do you see?

If you want, cut-and-paste this sample:

3x^2 - 2xy + y^2 = 5 + x,     3(x+4)^2 - 2(x+4)(y-7) + (y-7)^2 = 5 + (x+4)

Here's what WolframAlpha gives you, for this sample:

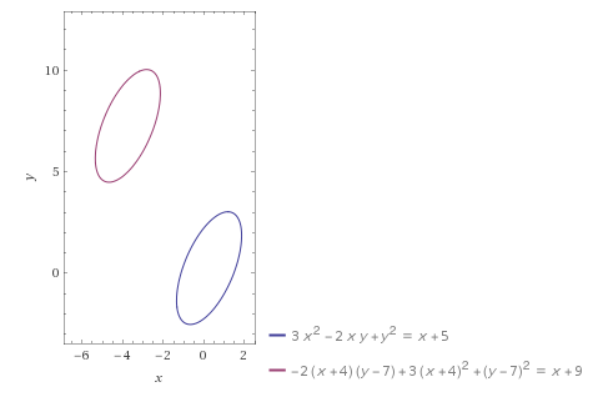
The blue is the graph of the first equation.
The purple is the graph of the second equation.

Replacing every $\,x\,$ by $\,x + 4\,$ shifted the blue graph LEFT $\,4\,$ units.
Replacing every $\,y\,$ by $\,y - 7\,$ shifted the blue graph UP $\,7\,$ units.
Both are counter-intuitive!

Example: Graphing a Shifted Conic

Graph: $\,x^2 + 6x + 12y + 3 = 0\,$

Solution:

To determine the type of conic, compare with $\,Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\,$ and use the conic discriminant.
Write ‘$\,x^2 + 6x + 12y + 3 = 0\,$’ as:   $\,1x^2 + 0xy + 0y^2 + 6x + 12y + 3 = 0\,$
Thus: $\,A = 1\,,$ $\,B = 0\,,$ $\,C = 0\,$
$B^2 - 4AC = 0^2 - 4(1)(0) = 0\,$
This is a parabola.

Using information about parabolas, the corresponding standard form is $\,x^2 = 4py\,.$
(If there was a $\,y^2\,$ term instead of an $\,x^2\,$ term, then the corresponding standard form would be $\,y^2 = 4px\,.$ )

We need to rewrite $\,x^2 + 6x + 12y + 3 = 0\,$ in the form $\,(x+a)^2 = 4p(y+b)\,$ for appropriate constants $\,a\,$ and$\,b\,.$

Complete the square on $\,x\,,$ and move the other terms to the right side: $$ \begin{alignat}{2} &\cssId{s133}{x^2 + 6x + 12y + 3 = 0}&\qquad&\cssId{s134}{\text{(original equation)}}\cr\cr &\cssId{s135}{x^2 + 6x \qquad\qquad = -12y - 3}&&\cssId{s136}{\text{(leave space for the correct number to complete the square)}}\cr\cr &\cssId{s137}{x^2 + 6x + \bigl(\frac{6}{2}\bigr)^2 = -12y - 3 + 9}&&\cssId{s138}{\text{(take coefficient of $\,x\,$ term, divide by $\,2\,,$ square; add to both sides)}}\cr\cr &\cssId{s139}{(x+3)^2 = -12y + 6}&&\cssId{s140}{\text{(write left side as a perfect square)}}\cr\cr &\cssId{s141}{(x+3)^2 = \color{red}{-12}y + 6\cdot\frac{\color{red}{-12}}{-12}}&&\cssId{s142}{\text{(multiply by $\,1\,$ on right side to make it easier to factor in next step)}}\cr\cr &\cssId{s143}{(x + 3)^2 = -12(y - \frac 12)}&&\cssId{s144}{\text{(factor $\,-12\,$ out of right side)}} \end{alignat} $$ At this point, you would graph the unshifted version, $\,x^2 = -12y\,,$ using standard techniques.
Then, shift left $\,3\,$ (replace $\,x\,$ by $\,x + 3\,$) and up $\,\frac 12\,$ (replace $\,y\,$ by $\,y - \frac 12\,$).
Done!!

Alternative Language for Shifting Up/Down/Left/Right

Sometimes it's easier to use different language for shifting:

This alternative language is used in some of the exercises below.

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
polar coordinates


On this exercise, you will not key in your answer.
However, you can check to see if your answer is correct. 		PROBLEM TYPES:
1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18
AVAILABLE MASTERED
IN PROGRESS

(MAX is 18; there are 18 different problem types.)
Want textboxes to type in your answers? Check here: