Equations of Ellipses in Standard Form:
Foci on the $\,x$-axis

Preliminary Notation and Observations

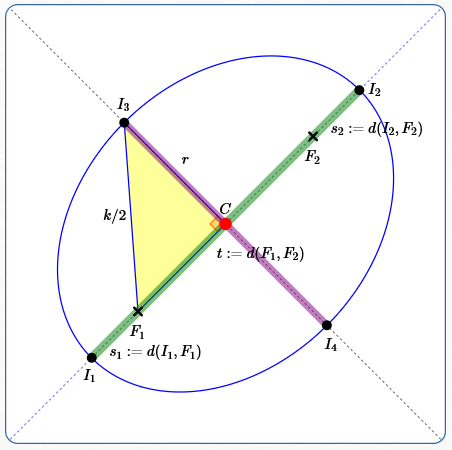
Consider an ellipse with foci $\,F_1\,$ and $\,F_2\,$ and ellipse constant $\,k\,.$ Follow along with the sketch at right as you read these observations. By the definition of ellipse, every point $\,P\,$ on the ellipse satisfies: $$\cssId{s13}{d(P,F_1) + d(P,F_2) = k}$$ Here, $\,d(A,B)\,$ denotes the distance between points $\,A\,$ and $\,B\,.$ Vertices of an Ellipse: Let $\,I_1\,$ and $\,I_2\,$ denote the intersection points of: the ellipse the line through the foci By definition, $\,I_1\,$ and $\,I_2\,$ are called the vertices of the ellipse. Major Axis of an Ellipse: By definition, the major axis of the ellipse is the line segment from $\,I_1\,$ to $\,I_2\,.$ The major axis is shown at right in green. The distance from $\,I_1\,$ to $\,F_1\,$ is the same as the distance from $\,I_2\,$ to $\,F_2\,.$ Here's a proof: Define $\,s_1 := d(I_1,F_1)\,,$ $\,s_2 := d(I_2,F_2)\,,$ and $\,t := d(F_1,F_2)\,.$ Since $\,I_1\,$ is on the ellipse, $\,d(I_1,F_1) + d(I_1,F_2) = k\,.$ That is, $\,s_1 + (s_1 + t) = k\,.$ Similarly, since $\,I_2\,$ is on the ellipse, $\,s_2 + (s_2 + t) = k\,.$ Solving $\,2s_1 + t = k\,$ and $\,2s_2 + t = k\,$ simultaneously gives $\,s_1 = s_2 := s\,.$ the Length of the Major Axis is the Ellipse Constant: Using the proof above, the length of the major axis is $\,2s + t = k\,.$ Thus, an ellipse ‘shows’ its ellipse constant as the length of its major axis! Center of an Ellipse: Let $\,C\,$ denote the midpoint of the major axis. By definition, $\,C\,$ is called the center of the ellipse, and is shown at right in red. Minor Axis of an Ellipse: Draw the line through the center that is perpendicular to the major axis. Let $\,I_3\,$ and $\,I_4\,$ denote the intersection points of this line with the ellipse. By definition, the minor axis of the ellipse is the line segment from $\,I_3\,$ to $\,I_4\,.$ The minor axis is shown at right in purple. The Minor Axis is shorter than the Major Axis: Focus attention on the yellow right triangle. The hypotenuse has length $\,\frac k2\,.$ (Be sure that you can explain why!) Let $\,r := d(I_3,C)\,.$ Note that the length of the minor axis is $\,2r\,.$ Since each leg of a right triangle is strictly shorter than the hypotenuse: $$\begin{gather} \cssId{s43}{r < \frac k2}\cr\cr \cssId{s44}{\overbrace{2r}^{\text{length of minor axis}} < \overbrace{k}^{\text{length of major axis, ellipse constant}}} \end{gather} $$

$I_1\,$ and $\,I_2\,$ are the vertices of the ellipse; they are the intersection points of the ellipse and the line through the foci. The major axis of the ellipse is the line segment that connects the vertices. Its length is the ellipse constant, $\,k\,.$ An ellipse ‘shows’ its ellipse constant as the length of its major axis! The center of an ellipse is the midpoint of the major axis. You might roughly want to think of the major axis as giving the ‘length’ of the ellipse, and the minor axis (the segment from $\,I_3\,$ to $\,I_4\,$) as giving the ‘width’ of the ellipse. The major axis is always longer than the minor axis.

Derivation of the Equation of an Ellipse:
Center at the Origin, Foci on the $x$-axis

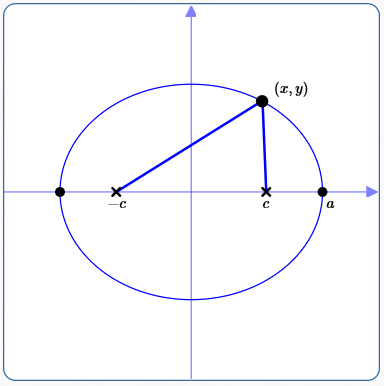
Position the ellipse: As shown at right, position an ellipse with center at the origin and foci (marked with ‘x’) on the $x$-axis. Notation ($\,c\,$ and $\,a\,$): Define: $c = \,$ the distance from the center (the origin) to each focus. Since $\,c\,$ is a distance, $\,c > 0\,.$ The coordinates of the foci are therefore $\,(c,0)\,$ and $\,(-c,0)\,.$ $a = \,$ the distance from the center to each vertex. Since $\,a\,$ is a distance, $\,a > 0\,.$ The coordinates of the vertices are therefore $\,(a,0)\,$ and $\,(-a,0)\,.$ Ellipse constant: The ellipse constant is the length of the major axis, which is $\,2a\,.$ Use the definition of ellipse on a typical point: Let $\,(x,y)\,$ be a typical point on the ellipse, so that the sum of its distances to the foci is the ellipse constant ($\,2a\,$). That is, $$ \cssId{s72}{\biggl( \text{distance from } (x,y) \text{ to } (-c,0) \biggr) + \biggl( \text{distance from } (x,y) \text{ to } (c,0) \biggr) = 2a} $$ Use the distance formula and make obvious simplications: $$ \begin{gather} \cssId{s74}{\sqrt{\bigl(x - (-c)\bigr)^2 + \bigl(y-0\bigr)^2} + \sqrt{\bigl(x - c\bigr)^2 + \bigl(y-0\bigr)^2} = 2a}\cr\cr \cssId{s75}{\sqrt{\bigl(x + c\bigr)^2 + y^2} + \sqrt{\bigl(x - c\bigr)^2 + y^2} = 2a} \qquad \cssId{s76}{(*)} \end{gather} $$

• A radical equation results:
  Equation (*) is a radical equation in two variables ($\,x\,$ and $\,y\,$).
  A radical equation, by definition, has at least one variable ‘inside’ a radical.
  A standard approach for working with radical equations is to ‘isolate and undo’.
  To isolate an expression (like a radical) means to get it all by itself on one side of the equation.
  Be on the lookout for this ‘isolate and undo’ sequence (used twice!) in the algebraically-intensive simplifying procedure below.
• ‘Undoing’ a square root:
  For us, the radicals that appear in (*) are square roots; a square root is ‘undone’ by squaring.
  That is:  for all $\,t \ge 0\,,$ $\,(\,\sqrt t\,)^2 = t\,.$ By squaring a square root, the square root disapppears!
• The expressions under the square roots in (*) are nonnegative:
  For all real numbers $\,x\,,$ $\,y\,$ and $\,c\,,$ both expressions under the square roots in (*) are nonnegative:
  • $(x+c)^2 + y^2 \ge 0$
  • $(x-c)^2 + y^2 \ge 0$
  Why?
  Squared quantities are always nonnegative: for all real numbers $\,t\,,$ $\,t^2 \ge 0\,.$
  Also, sums of nonnegative quantities are nonnegative.
• Apply the ‘isolate and undo’ technique to (*):
  We'll choose to isolate the first square root that appears (going from left to right) in (*).
  It's conventional to isolate it (i.e., get it all by itself) on the left-hand side of the equation.
  It doesn't matter which square root we isolate first, but a choice had to be made.
  There's a lot of algebra here, so breathe deeply and take your time!
  $$ \begin{alignat}{2} &\cssId{s102}{\sqrt{\bigl(x + c\bigr)^2 + y^2} = 2a - \sqrt{\bigl(x - c\bigr)^2 + y^2}}&\qquad&\cssId{s103}{\text{(isolate the first square root)}}\cr\cr &\cssId{s104}{(x+c)^2 + y^2 = \left( 2a - \sqrt{\bigl(x - c\bigr)^2 + y^2} \right)^2}&&\cssId{s105}{\text{(‘undo’ the isolated square root by squaring both sides)}}\cr\cr &\cssId{s106}{(x+c)^2 + y^2 = (2a)^2 - 2\cdot 2a\sqrt{\bigl(x - c\bigr)^2 + y^2} + \left(\sqrt{\bigl(x - c\bigr)^2 + y^2}\right)^2}&&\cssId{s107}{\text{(FOIL the right-hand side)}}\cr\cr &\cssId{s108}{(x+c)^2 + y^2 = 4a^2 - 4a\sqrt{\bigl(x - c\bigr)^2 + y^2} + (x-c)^2 + y^2}&&\cssId{s109}{\text{(simplify)}}\cr\cr &\cssId{s110}{\color{red}{x^2} + 2cx + \color{red}{c^2} + \color{red}{y^2} = 4a^2 - 4a\sqrt{\bigl(x - c\bigr)^2 + y^2} + \color{red}{x^2} - 2cx + \color{red}{c^2} + \color{red}{y^2}}&&\cssId{s111}{\text{(FOIL)}}\cr\cr &\cssId{s112}{2cx = 4a^2 - 4a\sqrt{\bigl(x - c\bigr)^2 + y^2} - 2cx} &&\cssId{s113}{\text{(subtract $\,\color{red}{x^2 + c^2 + y^2}\,$ from both sides)}}\cr\cr &\cssId{s114}{\color{red}{4}a\sqrt{\bigl(x - c\bigr)^2 + y^2} = \color{red}{4}a^2 - \color{red}{4}cx} &&\cssId{s115}{\text{(isolate the remaining square root term)}}\cr\cr &\cssId{s116}{a\sqrt{\bigl(x - c\bigr)^2 + y^2} = a^2 - cx} &&\cssId{s117}{\text{(divide by $\,\color{red}{4}$)}}\cr\cr &\cssId{s118}{\left( a\sqrt{\bigl(x - c\bigr)^2 + y^2}\right)^2 = (a^2 - cx)^2} &&\cssId{s119}{\text{(square both sides)}}\cr\cr &\cssId{s120}{a^2 \bigl( (x - c\bigr)^2 + y^2\ \bigr) = (a^2 - cx)^2} &&\cssId{s121}{\text{(multiply out the left-hand side)}}\cr\cr &\cssId{s122}{a^2 \bigl( x^2 - 2cx + c^2 + y^2 \bigr) = a^4 - 2a^2cx + c^2x^2} &&\cssId{s123}{\text{(FOIL)}}\cr\cr &\cssId{s124}{a^2x^2 \color{red}{- 2a^2cx} + a^2c^2 + a^2y^2 = a^4 \color{red}{- 2a^2cx} + c^2x^2} &&\cssId{s125}{\text{(distributive law)}}\cr\cr &\cssId{s126}{a^2x^2 + a^2c^2 + a^2y^2 = a^4 + c^2x^2} &&\cssId{s127}{\text{(add $\,\color{red}{2a^2cx}\,$ to both sides)}}\cr\cr &\cssId{s128}{a^2x^2 - c^2x^2 + a^2y^2 = a^4 - a^2c^2} &&\cssId{s129}{\text{(re-arrange: variable terms on left, constant terms on right)}}\cr\cr &\cssId{s130}{(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)} \qquad\qquad \cssId{s131}{(\dagger)}&&\cssId{s132}{\text{(factor)}}\cr\cr \end{alignat} $$

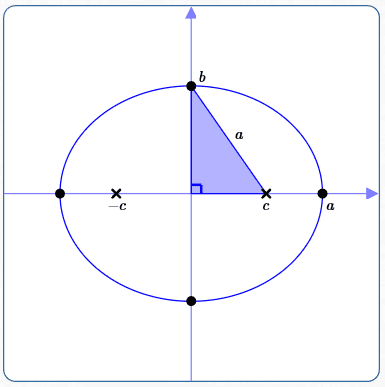
At this point, we need additional notation and observations. Notation ($\,b\,$): Define $\,b\,$ as the distance from the center to an endpoint of the minor axis. Since $\,b\,$ is a distance, $\,b > 0\,.$ The coordinates of the minor axis endpoints are therefore $\,(0,b)\,$ and $\,(0,-b)\,.$ The blue triangle involves $\,a\,,$ $\,b\,$ and $\,c\,$: Focus attention on the blue triangle at right. It is a right triangle; the legs have lengths $\,b\,$ and $\,c\,.$ The hypotenuse is half the ellipse constant, and hence has length $\,\frac{2a}{2} = a\,.$ Get the relationship between $\,a\,,$ $\,b\,$ and $\,c\,$: By the Pythagorean Theorem, we have $\,c^2 + b^2 = a^2\,.$ Equivalently, $\,b^2 = a^2 - c^2\,$ and $\,c^2 = a^2 - b^2\,.$

• $\,a\,$ is greater than $\,b\,$:
  Since the major axis is always longer than the minor axis, $\,a > b\,.$
  Alternatively: $$ \begin{alignat}{2} \cssId{s148}{a^2}\ & \cssId{s149}{= b^2 + c^2} &\qquad &\cssId{s150}{\text{(relationship between $\,a\,,$ $\,b\,$ and $\,c\,$)}}\cr &\cssId{s151}{> (b^2 + c^2) - c^2} &&\cssId{s152}{\text{(subtracting a positive number, $\,c^2\,,$ from the right side makes it smaller)}}\cr &\cssId{s153}{= b^2} \end{alignat} $$ Thus, $\,a^2 > b^2\,.$
  Since both $\,a\,$ and $\,b\,$ are positive, $\,a^2 > b^2\,$ implies $\,a > b\,.$
• We want to end up with an equation involving visible attributes:
  Right now, equation ($\dagger$) involves the constants $\,a\,$ and $\,c\,.$
  Here's the problem: when you look at a typical ellipse, you can't ‘see’ $\,c\,.$
  You can see $\,a\,,$ because it's half the length of the major axis.
  You can see $\,b\,,$ because it's half the length of the minor axis.
  But, the location of the foci (which is what $\,c\,$ tells us) is often hidden.
  So, it would be more desirable to have the equation of the ellipse involve only $\,a\,$ and $\,b\,.$
• Rewrite ($\dagger$) to eliminate $\,c\,,$ and simplify:
  To this end, use $\,b^2 = a^2 - c^2\,$ to rewrite ($\dagger$): $$ \cssId{s167}{b^2x^2 + a^2y^2 = a^2b^2} $$ Note that $\,a > 0\,$ and $\,b > 0\,,$ so $\,ab > 0\,$ and hence $\,a^2b^2 > 0\,.$
  Dividing both sides by $\,a^2b^2\,$ gives: $$ \begin{gather} \cssId{s170}{\frac{b^2x^2}{a^2b^2} + \frac{a^2y^2}{a^2b^2} = \frac{a^2b^2}{a^2b^2}}\cr\cr \cssId{s171}{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1}\cr\cr \end{gather} $$
• Summary:
  The equation of an ellipse with center at the origin and foci along the $\,x$-axis is $$ \cssId{s174}{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1} $$ where:

  $a > b > 0$ The length of the major axis (which lies on the $\,x$-axis) is $\,2a\,.$ The length of the minor axis (which lies on the $\,y$-axis) is $\,2b\,.$ The foci are determined by solving the equation $\,c^2 = a^2 - b^2\,$ for $\,c\,.$ The coordinates of the foci are $\,(-c,0)\,$ and $\,(c,0)\,.$ Note: the foci are on the $\color{red}{x}$-axis, and the bigger number ($\,a^2 > b^2\,$) is beneath the $\,\color{red}{x}^2\,.$