Definition of an Ellipse

Ellipses were introduced in Introduction to Conic Sections,
as one of several different curves (‘conic sections’) that are formed by intersecting a plane with an infinite double cone.

Identifying Conics by the Discriminant introduced the general equation for any conic section,
and gave conditions under which the graph would be an ellipse.

In this current section, we present and explore the standard definition of an ellipse.
This definition facilitates the derivation of standard equations for ellipses.

Recall that the notation ‘$\,d(P,Q)\,$’ denotes the distance between points $\,P\,$ and $\,Q\,.$

DEFINITION ellipse

An ellipse is the set of points in a plane such that the sum of the distances to two fixed points
is constant.

More precisely:

Let $\,F_1\,$ and $\,F_2\,$ be points;
they are called the foci of the ellipse (pronounced FOE-sigh).
(The singular form of ‘foci’ is ‘focus’.)
Let $\,k\,$ be a positive real number, with $\,k > d(F_1,F_2)\,.$
In this section, $\,k\,$ is referred to as the ellipse constant.

The ellipse determined by $\,F_1\,,$ $\,F_2\,$ and $\,k\,$ is the set of all points $\,P\,$ in a plane such that: $$ \cssId{s18}{\overbrace{d(P,F_1) + d(P,F_2)}^{\text{the sum of the distances to two fixed points}}} \quad \cssId{s19}{\overbrace{=\strut}^{\text{is}}}\quad \cssId{s20}{\overbrace{k}^{\text{constant}}}$$

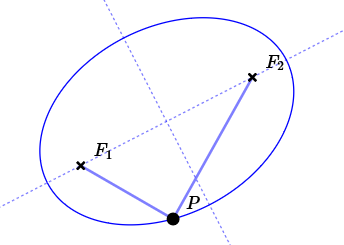
$\,P\,$ is a general point on the ellipse.

$\,d(P,F_1) + d(P,F_2) = \text{constant}$

Old-Fashioned Playing with the Definition of an Ellipse

Got a piece of cardboard, paper, tape, string/cord (not stretchy), and pen/pencil?
Then, you can create your own ellipse:

Tape the paper to the cardboard (at the corners is sufficient).
Punch two small holes through the paper/cardboard at the desired foci.
Put the cord/string through the two holes from front to back, and tie securely on the back. The length of the string that protrudes in the front, when held taut by a pen (see photo), is the ellipse constant.
Keeping the string taut, trace the ellipse.
(The string gets a bit twisted near the line through the two foci.
So, draw one continuous motion for the upper half, then re-position and draw the lower half.)

(The sunflower in a vase is optional. ☺
I grew my own sunflowers from seed in 2017, when I was writing this section!)

More Playing with the Definition of an Ellipse

You can also play with ellipses using the dynamic JSXGraph at right:

$F_1\,$ and $\,F_2\,$ are the foci. Move them around!
As you hover over each focus, you can see the coordinates of the point.
The slider at the top sets the ellipse constant.
The slider can be set to numbers between $\,0\,$ and $\,20\,$ with increments of $\,0.5\,.$
The starting value is $\,12\,$ (refresh the page as needed).
The current distance between the foci is displayed near the top.
Watch this distance change as you move the foci around.
The starting value for $\,d(F_1,F_2)\,$ is $\,10\,$ (refresh the page as needed).
In order to see an ellipse, the ellipse constant (slider value) must be greater than the distance between the foci.
$\,P\,$ is a general point on the ellipse. Move it around!
When the ellipse constant equals the distance between the foci, the ‘ellipse’ degenerates to a line segment.
Ignore the line segment that you see when the ellipse constant $\,k\,$ is less than the distance between the foci. As discussed below, in this case there are actually no points $\,P\,$ that satisfy $\,d(F_1,P) + d(F_2,P) = k\,.$

Notes:

In the definition of ellipse, the ellipse constant $\,k\,$ is required to be
strictly greater than the distance between the two foci.

Why?
As shown below, other values of $\,k\,$ don't give anything that a reasonable person would want to call an ellipse!

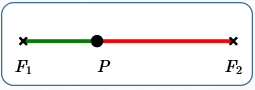
A ‘LINE SEGMENT’ ELLIPSE: $\,k = d(F_1,F_2)\,$

Suppose the ellipse constant, $\,k\,,$ equals the distance between the foci:
that is, $\,k = d(F_1,F_2)\,.$

In this case, the solution set to the equation $$ \cssId{s62}{\color{green}{d(P,F_1)} + \color{red}{d(P,F_2)} = k} $$ is the line segment between $\,F_1\,$ and $\,F_2\,$ (including the endpoints).
Most people don't want to call a line segment an ellipse!
This is why $\,k\,$ is not allowed to equal $\,d(F_1,F_2)\,$ in the definition of ellipse.

$\,\color{green}{d(P,F_1)}\,$ is the length of the green segment
$\,\color{red}{d(P,F_2)}\,$ is the length of the red segment
together, the green and red segments give $\,d(F_1,F_2)\,$

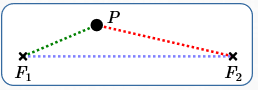
AN ‘EMPTY’ ELLIPSE: $\,k < d(F_1,F_2)\,$

The shortest distance between any two points is a straight line.

In particular, the shortest distance from $\,F_1\,$ to $\,F_2\,$ is the length of the line segment between them,
and is denoted by $\,d(F_1,F_2)\,.$

Thus, any path from $\,F_1\,$ to $\,F_2\,$ must have length greater than or equal to $\,d(F_1,F_2)\,.$

In particular (refer to sketch at right),
the piecewise-linear path from $\,F_1\,$ to $\,P\,$ and then from $\,P\,$ to $\,F_2\,$
always has length greater than or equal to $\,d(F_1,F_2)\,.$

Therefore, if the ellipse constant $\,k\,$ is strictly less than $\,d(F_1,F_2)\,,$
there are no points $\,P\,$ that make the following equation true: $$ \cssId{s79}{\overbrace{d(P,F_1) + d(P,F_2)\strut }^{\text{always $\,\,\ge\,\, d(F_1,F_2)$}}} \qquad \cssId{s80}{=}\qquad \cssId{s81}{\overbrace{\strut k}^{< \,\, d(F_1,F_2)}} $$ You might want to call this an empty ellipse, an invisible ellipse, or an imaginary ellipse!
There's nothing there!

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Reflecting Property of an Ellipse