Equations of Hyperbolas in Standard Form

Hyperbolas were introduced in two prior lessons:

In this current section, a hyperbola is positioned with its center at the origin and foci on the $x$-axis or $y$-axis.
These placements result in the so-called ‘standard forms’ for a hyperbola, which—as you'll see—are very simple equations!

If you're short on time, jump right to the summary of equations of hyperbolas.

Review and Additional Notation

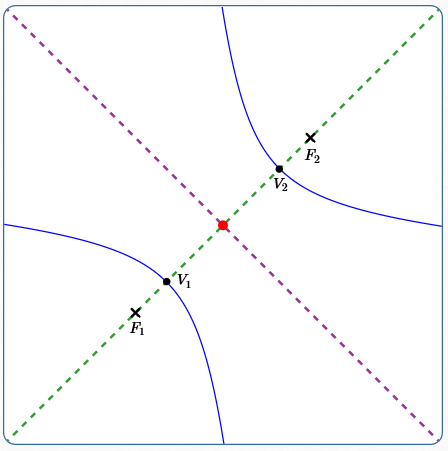
Consider a hyperbola with foci $\,F_1\,$ and $\,F_2\,$ and hyperbola constant $\,k\,.$

Recall from the previous section that:

By the definition of hyperbola, every point $\,P\,$ on the hyperbola satisfies: $$\cssId{s11}{|d(P,F_1) - d(P,F_2)| = k}$$ Here, $\,d(A,B)\,$ denotes the distance between points $\,A\,$ and $\,B\,.$
The major axis of a hyperbola is the line through the foci, shown at right dashed green.
The vertices of a hyperbola are the two points where the hyperbola intersects its major axis. At right, they are denoted by $\,V_1\,$ and $\,V_2\,$ (with $\,V_1\,$ closest to $\,F_1\,$).
A hyperbola ‘shows’ its hyperbola constant as the distance between the vertices.
That is, $\,d(V_1,V_2) = k\,.$

Here is some additional notation:

Center of a Hyperbola:
Let $\,C\,$ denote the midpoint of the line segment from $\,F_1\,$ to $\,F_2\,.$
By definition, $\,C\,$ is the center of the hyperbola, and is shown at right in red.
Minor Axis of a Hyperbola:
The minor axis of a hyperbola is the perpendicular bisector of the line segment between the foci. Equivalently, the minor axis is the line through the center that is perpendicular to the major axis. The minor axis is shown at right dashed purple.

The major axis of the hyperbola is the line through the foci; it is dashed green.

The center of the hyperbola is the midpoint of the line segment connecting the foci; it is shown in red.

The minor axis of the hyperbola is the line through the center that is perpendicular to the major axis;
it is dashed purple.

Derivation of the Equation of a Hyperbola:
Center at the Origin, Foci on the $x$-axis

Position the hyperbola:
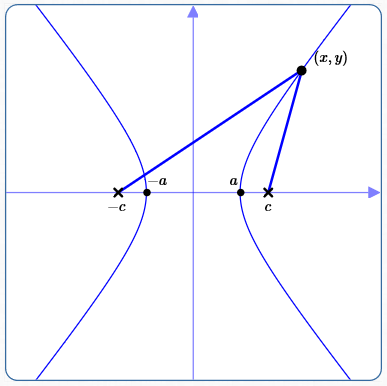
As shown at right, position a hyperbola with center at the origin
and foci (marked with ‘x’) on the $x$-axis.
With this positioning, the $x$-axis is the major axis; the $y$-axis is the minor axis.
Notation ($\,c\,$ and $\,a\,$):
Define:
- $c := \,$ the distance from the center (the origin) to each focus.
  Since $\,c\,$ is a distance, $\,c > 0\,.$
  The coordinates of the foci are therefore $\,(c,0)\,$ and $\,(-c,0)\,.$
- $a := \,$ the distance from the center to each vertex.
  Since $\,a\,$ is a distance, $\,a > 0\,$; also, $\,a < c\,.$
  The coordinates of the vertices are therefore $\,(a,0)\,$ and $\,(-a,0)\,.$
(Recall that ‘$\,:=\,$’ means ‘equal, by definition’.)
Hyperbola constant:
The hyperbola constant is the distance between the vertices, which is $\,2a\,.$

Hyperbola with foci on $x$-axis
and center at the origin

$c := \,$ distance from center to each focus
$a := \,$ distance from center to each vertex
Note that $\,0 < a < c\,.$

Use the definition of hyperbola on a typical point:
Let $\,(x,y)\,$ be a typical point on the hyperbola.
Thus, the difference of its distances to the foci is the hyperbola constant, $\,2a\,.$
That is, $$ \cssId{s52}{\biggl|\bigl( \text{distance from } (x,y) \text{ to } (-c,0) \bigr) - \bigl( \text{distance from } (x,y) \text{ to } (c,0) \bigr)\biggr| = 2a} $$ Use the distance formula and make obvious simplications: $$ \begin{gather} \cssId{s54}{\biggl|\sqrt{\bigl(x - (-c)\bigr)^2 + \bigl(y-0\bigr)^2} - \sqrt{\bigl(x - c\bigr)^2 + \bigl(y-0\bigr)^2}\biggr| = 2a}\cr\cr \cssId{s55}{\biggl|\sqrt{\bigl(x + c\bigr)^2 + y^2} - \sqrt{\bigl(x - c\bigr)^2 + y^2}\biggr| = 2a} \qquad \cssId{s56}{(*)} \end{gather} $$

Get rid of the absolute values:
Recall that for $\,k\ge 0\,,$ $\,|x| = k\,$ is equivalent to $\,x=\pm k\,.$
Use this fact to get rid of the absolute value symbols in (*): $$ \cssId{s60}{\sqrt{\bigl(x + c\bigr)^2 + y^2} - \sqrt{\bigl(x - c\bigr)^2 + y^2} = \pm 2a} \qquad \cssId{s61}{(**)} $$ Make sure you appreciate the compactness that the ‘plus or minus’ symbol ‘$\,\pm\,$’ provides!
Without it, (**) would need to be written as $$ \cssId{s64}{\sqrt{\bigl(x + c\bigr)^2 + y^2} - \sqrt{\bigl(x - c\bigr)^2 + y^2} = 2a} \quad \cssId{s65}{\text{or}} \quad \cssId{s66}{\sqrt{\bigl(x + c\bigr)^2 + y^2} - \sqrt{\bigl(x - c\bigr)^2 + y^2} = -2a} $$ Here's the good news—that bothersome ‘plus or minus’ symbol will disappear soon!
A radical equation results:
Equation (**) is a radical equation in two variables ($\,x\,$ and $\,y\,$).
A radical equation, by definition, has at least one variable ‘inside’ a radical.
A standard approach for working with radical equations is to ‘isolate and undo’.
To isolate an expression (like a radical) means to get it all by itself on one side of the equation.
Be on the lookout for this ‘isolate and undo’ sequence (used twice!) in the algebraically-intensive simplifying procedure below.
‘Undoing’ a square root:
For us, the radicals that appear in (**) are square roots; a square root is ‘undone’ by squaring.
That is: for all $\,t \ge 0\,,$ $\,(\,\sqrt t\,)^2 = t\,.$ By squaring a square root, the square root disapppears!
The expressions under the square roots in (**) are nonnegative:
For all real numbers $\,x\,,$ $\,y\,$ and $\,c\,,$ both expressions under the square roots in (**) are nonnegative:
- $(x+c)^2 + y^2 \ge 0$
- $(x-c)^2 + y^2 \ge 0$
Why?
Squared quantities are always nonnegative: for all real numbers $\,t\,,$ $\,t^2 \ge 0\,.$
Also, sums of nonnegative quantities are nonnegative.
Apply the ‘isolate and undo’ technique to (**):
We'll choose to isolate the first square root that appears (going from left to right) in (**).
It's conventional to isolate it (i.e., get it all by itself) on the left-hand side of the equation.
It doesn't matter which square root we isolate first, but a choice had to be made.
There's a lot of algebra here, so breathe deeply and take your time!
$$ \begin{alignat}{2} &\cssId{s93}{\sqrt{\bigl(x + c\bigr)^2 + y^2} = \pm 2a + \sqrt{\bigl(x - c\bigr)^2 + y^2}}&\qquad&\cssId{s94}{\text{(isolate the first square root)}}\cr\cr &\cssId{s95}{(x+c)^2 + y^2 = \left( \pm 2a + \sqrt{\bigl(x - c\bigr)^2 + y^2} \right)^2}&&\cssId{s96}{\text{(‘undo’ the isolated square root by squaring both sides)}}\cr\cr &\cssId{s97}{(x+c)^2 + y^2 = (\pm 2a)^2 + 2\cdot (\pm 2a)\cdot\sqrt{\bigl(x - c\bigr)^2 + y^2} + \left(\sqrt{\bigl(x - c\bigr)^2 + y^2}\right)^2}&&\cssId{s98}{\text{(FOIL the right-hand side)}}\cr\cr &\cssId{s99}{(x+c)^2 + y^2 = 4a^2 \pm 4a\sqrt{\bigl(x - c\bigr)^2 + y^2} + (x-c)^2 + y^2}&&\cssId{s100}{\text{(simplify; note that both $\,(2a)^2\,$ and $\,(-2a)^2\,$ give $\,4a^2\,$)}}\cr\cr &\cssId{s101}{\color{red}{x^2} + 2cx + \color{red}{c^2} + \color{red}{y^2} = 4a^2 \pm 4a\sqrt{\bigl(x - c\bigr)^2 + y^2} + \color{red}{x^2} - 2cx + \color{red}{c^2} + \color{red}{y^2}}&&\cssId{s102}{\text{(FOIL)}}\cr\cr &\cssId{s103}{2cx = 4a^2 \pm 4a\sqrt{\bigl(x - c\bigr)^2 + y^2} - 2cx} &&\cssId{s104}{\text{(subtract $\,\color{red}{x^2 + c^2 + y^2}\,$ from both sides)}}\cr\cr &\cssId{s105}{-\bigl(\pm 4a\sqrt{\bigl(x - c\bigr)^2 + y^2}\bigr) = 4a^2 - 4cx} &&\cssId{s106}{\text{(isolate the remaining square root term)}}\cr\cr &\cssId{s107}{\mp \color{red}{4}a\sqrt{\bigl(x - c\bigr)^2 + y^2} = \color{red}{4}a^2 - \color{red}{4}cx} &&\cssId{s108}{\text{(simplify notation: replace $\,-(\pm)\,$ with $\,\mp\,$)}}\cr\cr &\cssId{s109}{\mp a\sqrt{\bigl(x - c\bigr)^2 + y^2} = a^2 - cx} &&\cssId{s110}{\text{(divide by $\,\color{red}{4}$)}}\cr\cr &\cssId{s111}{\left( \mp a\sqrt{\bigl(x - c\bigr)^2 + y^2}\right)^2 = (a^2 - cx)^2} &&\cssId{s112}{\text{(square both sides)}}\cr\cr &\cssId{s113}{a^2 \bigl( (x - c\bigr)^2 + y^2\ \bigr) = (a^2 - cx)^2} &&\cssId{s114}{\text{(multiply out the left-hand side)}}\cr\cr &\cssId{s115}{a^2 \bigl( x^2 - 2cx + c^2 + y^2 \bigr) = a^4 - 2a^2cx + c^2x^2} &&\cssId{s116}{\text{(FOIL)}}\cr\cr &\cssId{s117}{a^2x^2 - \color{red}{2a^2cx} + a^2c^2 + a^2y^2 = a^4 - \color{red}{2a^2cx} + c^2x^2} &&\cssId{s118}{\text{(distributive law)}}\cr\cr &\cssId{s119}{a^2x^2 + a^2c^2 + a^2y^2 = a^4 + c^2x^2} &&\cssId{s120}{\text{(add $\,\color{red}{2a^2cx}\,$ to both sides)}}\cr\cr &\cssId{s121}{a^2x^2 - c^2x^2 + a^2y^2 = a^4 - a^2c^2} &&\cssId{s122}{\text{(re-arrange: variable terms on left, constant terms on right)}}\cr\cr &\cssId{s123}{c^2x^2 - a^2x^2 - a^2y^2 = a^2c^2 - a^4} &&\cssId{s124}{\text{(multiply both sides by $\,-1\,$)}}\cr\cr &\cssId{s125}{(c^2 - a^2)x^2 - a^2y^2 = a^2(c^2 - a^2)} \qquad\qquad \cssId{s126}{(\dagger)}&&\cssId{s127}{\text{(factor)}}\cr\cr \end{alignat} $$
Notation ($\,b\,$):
Since $\,0 < a < c\,,$ we have $\,a^2 < c^2\,,$ so that $\,c^2 - a^2 > 0\,.$
Define $\,b\,$ to be the positive number such that $\,b^2 = c^2 - a^2\,.$
Note that $\,b\,$ is strictly greater than zero.
Rewrite ($\dagger$) to eliminate $\,c\,,$ and simplify:
Use $\,b^2 = c^2 - a^2\,$ to rewrite ($\dagger$): $$ \cssId{s136}{b^2x^2 - a^2y^2 = a^2b^2} $$ Note that $\,a > 0\,$ and $\,b > 0\,,$ so $\,ab > 0\,$ and hence $\,a^2b^2 > 0\,.$
Dividing both sides by $\,a^2b^2\,$ gives: $$ \begin{gather} \cssId{s141}{\frac{b^2x^2}{a^2b^2} - \frac{a^2y^2}{a^2b^2} = \frac{a^2b^2}{a^2b^2}}\cr\cr \cssId{s142}{\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1}\cr\cr \end{gather} $$
Summary:
The equation of a hyperbola with center at the origin and foci along the $\,x$-axis is $$ \cssId{s145}{\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1} $$ where $\,b^2 := c^2 - a^2\,.$

The foci are determined by solving the equation $\,c^2 = a^2 + b^2\,$ for $\,c\,.$
The coordinates of the foci are $\,(-c,0)\,$ and $\,(c,0)\,.$
Be careful!
The variables $\,a\,,$ $\,b\,$ and $\,c\,$ are used for both ellipses and hyperbolas, but their relationship is different!
For ellipses, $\,c^2 = a^2 \color{red}{-} b^2\,.$
For hyperbolas, $\,c^2 = a^2 \color{red}{+} b^2\,.$

Derivation of the Equation of a Hyperbola:
Center at the Origin, Foci on the $y$-axis

The derivation of the equation of a hyperbola with center at the origin and foci on the $y$-axis is nearly identical to the derivation above.

Position the hyperbola:
As shown at right, position a hyperbola with center at the origin
and foci (marked with ‘x’) on the $y$-axis.
With this positioning, the $y$-axis is the major axis; the $x$-axis is the minor axis.
Notation ($\,c\,$ and $\,a\,$):
Define:
- $c := \,$ the distance from the center (the origin) to each focus.
  Since $\,c\,$ is a distance, $\,c > 0\,.$
  The coordinates of the foci are therefore $\,(0,c)\,$ and $\,(0,-c)\,.$
- $a := \,$ the distance from the center to each vertex.
  Since $\,a\,$ is a distance, $\,a > 0\,$; also, $\,a < c\,.$
  The coordinates of the vertices are therefore $\,(0,a)\,$ and $\,(0,-a)\,.$
Hyperbola constant:
The hyperbola constant is the distance between the vertices, which is $\,2a\,.$

Hyperbola with foci on $y$-axis
and center at the origin

$c := \,$ distance from center to each focus
$a := \,$ distance from center to each vertex
Note that $\,0 < a < c\,.$

Use the definition of hyperbola on a typical point:
Let $\,(x,y)\,$ be a typical point on the hyperbola.
Thus, the difference of its distances to the foci is the hyperbola constant, $\,2a\,.$
That is, $$ \biggl|\bigl( \text{distance from } (x,y) \text{ to } (0,-c) \bigr) - \bigl( \text{distance from } (x,y) \text{ to } (0,c) \bigr)\biggr| = 2a $$ Use the distance formula and make obvious simplications: $$ \begin{gather} \biggl|\sqrt{(x-0)^2 + \bigl(y-(-c)\bigr)^2} - \sqrt{\bigl(x - 0\bigr)^2 + \bigl(y-c\bigr)^2}\biggr| = 2a\cr\cr \biggl|\sqrt{x^2 + (y+c)^2} - \sqrt{x^2 + (y-c)^2}\biggr| = 2a \qquad (\text{***}) \end{gather} $$

Get rid of the absolute values:
Recall that for $\,k\ge 0\,,$ $\,|x| = k\,$ is equivalent to $\,x=\pm k\,.$
Use this fact to get rid of the absolute value symbols in (*): $$ \sqrt{x^2 + (y+c)^2} - \sqrt{x^2 + (y-c)^2} = \pm 2a \qquad (\text{****}) $$ Don't worry too much about the bothersome ‘plus or minus’ symbol—it will disappear soon!
Apply the ‘isolate and undo’ technique to (****):
We'll choose to isolate the first square root that appears (going from left to right) in (****). $$ \begin{alignat}{2} &\sqrt{x^2 + (y+c)^2} = \pm 2a + \sqrt{x^2 + (y-c)^2}&\qquad&\text{(isolate the first square root)}\cr\cr &x^2 + (y+c)^2 = \left( \pm 2a + \sqrt{x^2 + (y-c)^2} \right)^2&&\text{(‘undo’ the isolated square root by squaring both sides)}\cr\cr &x^2 + (y+c)^2 = (\pm 2a)^2 + 2\cdot (\pm 2a)\cdot\sqrt{x^2 + (y-c)^2} + \left(\sqrt{x^2 + (y-c)^2}\right)^2&&\text{(FOIL the right-hand side)}\cr\cr &x^2 + (y+c)^2 = 4a^2 \pm 4a\sqrt{x^2 + (y-c)^2} + x^2 + (y-c)^2&&\text{(simplify; note that both $\,(2a)^2\,$ and $\,(-2a)^2\,$ give $\,4a^2\,$)}\cr\cr &\color{red}{x^2} + \color{red}{y^2} + 2cy + \color{red}{c^2} = 4a^2 \pm 4a\sqrt{x^2 + (y-c)^2} + \color{red}{x^2} + \color{red}{y^2} - 2cy + \color{red}{c^2}&&\text{(FOIL)}\cr\cr &2cy = 4a^2 \pm 4a\sqrt{x^2 + (y-c)^2} - 2cy &&\text{(subtract $\,\color{red}{x^2 + y^2 + c^2}\,$ from both sides)}\cr\cr &\mp \color{red}{4}a\sqrt{x^2 + (y-c)^2} = \color{red}{4}a^2 - \color{red}{4}cy &&\text{(isolate the remaining square root term)}\cr\cr &\mp a\sqrt{x^2 + (y-c)^2} = a^2 - cy &&\text{(divide by $\,\color{red}{4}$)}\cr\cr &\left( \mp a\sqrt{x^2 + (y-c)^2}\right)^2 = (a^2 - cy)^2 &&\text{(square both sides)}\cr\cr &a^2 \bigl(\ x^2 + (y-c)^2\ \bigr) = (a^2 - cy)^2 &&\text{(multiply out the left-hand side)}\cr\cr &a^2 \bigl(x^2 + y^2 - 2cy + c^2 \bigr) = a^4 - 2a^2cy + c^2y^2 &&\text{(FOIL)}\cr\cr &a^2x^2 + a^2y^2 - \color{red}{2a^2cy} + a^2c^2 = a^4 - \color{red}{2a^2cy} + c^2y^2 &&\text{(distributive law)}\cr\cr &a^2x^2 + a^2y^2 + a^2c^2 = a^4 + c^2y^2 &&\text{(add $\,\color{red}{2a^2cy}\,$ to both sides)}\cr\cr &a^2x^2 - c^2y^2 + a^2y^2 = a^4 - a^2c^2 &&\text{(re-arrange: variable terms on left, constant terms on right)}\cr\cr &-a^2x^2 + c^2y^2 - a^2y^2 = a^2c^2 - a^4 &&\text{(multiply both sides by $\,-1\,$)}\cr\cr &(c^2 - a^2)y^2 - a^2x^2 = a^2(c^2 - a^2) \qquad\qquad (\dagger\dagger)&&\text{(factor and re-arrange)}\cr\cr \end{alignat} $$
Notation ($\,b\,$):
Since $\,0 < a < c\,,$ we have $\,a^2 < c^2\,,$ so that $\,c^2 - a^2 > 0\,.$
Define $\,b\,$ to be the positive number such that $\,b^2 = c^2 - a^2\,.$
Note that $\,b\,$ is strictly greater than zero.
Rewrite ($\dagger\dagger$) to eliminate $\,c\,,$ and simplify:
Use $\,b^2 = c^2 - a^2\,$ to rewrite ($\dagger\dagger$): $$ b^2y^2 - a^2x^2 = a^2b^2 $$ Note that $\,a > 0\,$ and $\,b > 0\,,$ so $\,ab > 0\,$ and hence $\,a^2b^2 > 0\,.$
Dividing both sides by $\,a^2b^2\,$ gives: $$ \begin{gather} \frac{b^2y^2}{a^2b^2} - \frac{a^2x^2}{a^2b^2} = \frac{a^2b^2}{a^2b^2}\cr\cr \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\cr\cr \end{gather} $$
Summary:
The equation of a hyperbola with center at the origin and foci along the $\,y$-axis is $$ \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 $$ where $\,b^2 := c^2 - a^2\,.$

The foci are determined by solving the equation $\,c^2 = a^2 + b^2\,$ for $\,c\,.$
The coordinates of the foci are $\,(0,-c)\,$ and $\,(0,c)\,.$

Summary:
Equations of hyperbolas with center at the origin
and foci on the $x$-axis or $y$-axis

In both cases:
$0 < a < c$
With the equations in standard form, the number $\,a^2\,$ is the denominator of the positive term.
The hyperbola constant is $\,2a\,.$
The foci are determined by solving the equation $\,c^2 = a^2 + b^2\,$ for $\,c\,.$

Be careful!
The variables $\,a\,,$ $\,b\,$ and $\,c\,$ are used for both ellipses and hyperbolas,
but their relationship is different!
For ellipses, $\,c^2 = a^2 \color{red}{-} b^2\,.$
For hyperbolas, $\,c^2 = a^2 \color{red}{+} b^2\,.$

Foci on the $x$-axis

Equation of Hyperbola: $$\cssId{s172}{\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1}$$ When the foci are on the $\color{red}{x}$-axis,
the $\,\color{red}{x^2}$-term is positive.
Coordinates of foci: $\,(-c,0)\,$ and $\,(c,0)\,$

Foci on the $y$-axis

Equation of Hyperbola: $$\cssId{s179}{\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1}$$ When the foci are on the $\color{red}{y}$-axis,
the $\,\color{red}{y^2}$-term is positive.
Coordinates of foci: $\,(0,-c)\,$ and $\,(0,c)\,$

TIPS:

The key to recognizing the equation of a hyperbola with center at the origin and foci on either the $x$-axis or $y$-axis is this:
- It has only $\,x^2\,,$ $\,y^2\,,$ and constant terms.
- When the $\,x^2\,$ and $\,y^2\,$ terms are on the same side of the equation, then they must have different signs.
In both equations, the vertices are easy to find.
Since the vertices and foci are both on the same axis (the major axis),
this is a good way to minimize memorization and let the equation ‘tell you’ where the foci lie:
- Set $\,y = 0\,$ in the equation $\,\displaystyle\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$ to get $\,x = \pm a\,.$
  The vertices are on the $x$-axis, hence so are the foci: the major axis is the $x$-axis.
- Set $\,x = 0\,$ in the equation $\,\displaystyle\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\,$ to get $\,y = \pm a\,.$
  The vertices are on the $y$-axis, hence so are the foci: the major axis is the $y$-axis.
To find the foci:
With the equations in standard form, $\,c^2\,$ is always the sum of the two denominators: $$\cssId{s199}{c^2 = (\text{denominator of $\,x^2\,$ term}) + (\text{denominator of $\,y^2\,$ term})}$$

EXAMPLE: Finding the Equation of a Hyperbola

Find the equation of the following hyperbola:

center at the origin
major axis is the $y$-axis, with vertices at $\,\pm 5\,$
containing the point $\,(3,5\sqrt{2})\,$

Also, find the coordinates of the foci.

Solution:

Since the major axis is along the $y$-axis, the form of the equation is $$ \cssId{s208}{\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1} $$
$\,a = 5\,$
Since $\,(3,5\sqrt{2})\,$ is on the graph: $$\begin{gather} \cssId{s211}{\frac{(5\sqrt{2})^2}{5^2} - \frac{3^2}{b^2} = 1}\cr\cr \cssId{s212}{2 - \frac{9}{b^2} = 1}\cr\cr \cssId{s213}{\frac{9}{b^2} = 1}\cr\cr \cssId{s214}{b^2 = 9} \end{gather} $$
The equation is: $$ \cssId{s216}{\frac{y^2}{25} - \frac{x^2}{9} = 1} $$
Foci:
$\,c^2 = a^2 + b^2 = 25 + 9 = 34\,,$ so $\,c = \sqrt{34}\,$
Coordinates of foci: $\,(0,-\sqrt{34})\,$ and $\,(0,\sqrt{34})\,$
(Note that $\,5 < \sqrt{34}\,,$ so the foci are ‘inside’ the hyperbola.)

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Graphing Hyperbolas