Introduction to Rational Functions

Index card: 35a

Polynomials aren't immediately useful for modeling the following behaviors:

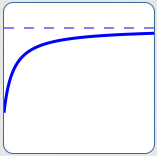
Outputs that approach a specific real number as $\,x\rightarrow\infty\,$ (or $\,x\rightarrow -\infty$)

Why not? For non-constant polynomials, when inputs get arbitrarily large, the outputs always get arbitrarily large.

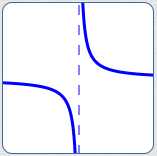
Outputs that ‘blow up’ (go to $\,\pm\infty\,$) as the input approaches a finite number

Why not? The only time that polynomial outputs can get arbitrarily large is when $\,x\rightarrow\pm\infty\,.$

Polynomials can still be useful in modeling these situations—we just need to allow them in the denominator! This produces a rational function, which is the subject of this section.

Example: A Rational Function; Its Domain

The function $\displaystyle\,f(x) = \frac{x^2 - 1}{2x + 3}\,$ is a rational function, since both the numerator and denominator are polynomials.

The domain of $\,f\,$ is the set of all real numbers $\,x\,$ for which the denominator is nonzero.

There's only one place where the denominator is equal to zero:

Therefore, the number $\,-\frac{3}{2}\,$ must be excluded from the domain of $\,f\,.$

Recall that the notation ‘$\text{dom}(f)\,$’ is used to denote the domain of $\,f\,.$ The domain can be conveniently described using either set-builder notation or interval notation:

Using set-builder notation:

$$\cssId{s28}{\text{dom}(f) = \{x\ |\ x\ne -\frac{3}{2}\}}$$

The domain of $\,f\,$ consists of two intervals of real numbers—the interval to the left of $-\frac{3}{2}\,$ and the interval to the right of $-\frac{3}{2}\,.$

Recall that the union symbol, ‘$\cup\,$’, is used to ‘combine’ two sets into a bigger set. Thus, using interval notation, we can alternatively write:

Notes About Rational Functions

RATIOnal functions—the name is a hint!

Observe that the word ‘rational’ contains the word RATIO (RATIOnal), to help remind you that rational functions are RATIOs. Ratios of what? Of polynomials! (... with appropriate restrictions on the denominator, of course ... )

Rational Functions Include Polynomials

According to the definition of rational function, every polynomial is a rational function. Why? Put the polynomial in the numerator, and put the constant function $\,Q(x) = 1\,$ in the denominator!

That is, for every polynomial $\,P\,,$ you can write $\,P(x) = \frac{P(x)}{1}\,,$ which is a ratio of polynomials.

Hence, the class of rational functions includes all polynomials. However, the name ‘rational function’ is usually reserved for rational functions that are not polynomials.

$y$-intercept of a Rational Function (set $\,x = 0\,,$ solve for $\,y\,$)

A $y$-intercept is where a graph crosses the $y$-axis.

Some people give a number when reporting a $y$-intercept—a value of $\,y\,$ where the graph hits the vertical axis. Other people give a point $\,(0,y)\,$ when reporting a $y$-intercept. Your choice!

Since a rational function is truly a function, it passes a vertical line test. So, if the graph of a rational function crosses the $y$-axis, then it crosses at exactly one point. If $\,x = 0\,$ is in the domain of a rational function, then the rational function has a unique $y$-intercept.

Every point on the $y$-axis has $\,x = 0\,.$ Thus, to find a $y$-axis intercept, set $\,x = 0\,$ and solve for $\,y\,.$ In other words, set the input equal to $\,0\,$ and find the corresponding output.

Example:  Find the $y$-intercept of $\,\displaystyle f(x) = \frac{x^2 - 1}{2x - 3}\,,$ providing it exists.

Solution:  $\displaystyle \cssId{s64}{f(0) = \frac{0-1}{0-3} = \frac 13}\,.$ The graph crosses the $y$-axis at $\,y = 1/3\,.$

$x$-intercept(s) of a Rational Function (set the numerator equal to zero, solve for $\,x\,$)

An $x$-intercept is where a graph crosses the $x$-axis.

Some people give a number when reporting an $x$-intercept—a value of $\,x\,$ where the graph hits the horizontal axis. Other people give a point $\,(x,0)\,$ when reporting an $x$-intercept. Your choice!

Functions can have any nonnegative integer number of $x$-intercepts: none, one, two, and so on.

Every point on the $x$-axis has $\,y = 0\,.$ Thus, to find $x$-axis intercept(s), set $\,y = 0\,$ and solve for $\,x\,.$ In other words, set the output equal to zero and solve for the corresponding input(s).

Rational functions are ratios (fractions) of polynomials. How can a fraction equal zero? Only when its numerator is zero (and its denominator is nonzero).

To find the $x$-intercept(s) of a rational function, do the following:

• Set the numerator equal to $\,0\,$ and solve for $\,x\,.$
• Check that these value(s) of $\,x\,$ are in the domain of the function. That is, check that these value(s) don't make the denominator equal to zero.

A value of $\,x\,$ where the graph of a function crosses the $x$-axis is also called a root or a zero of the function.

If $\displaystyle\,R(x) = \frac{N(x)}{D(x)}\,$ is a rational function, then the following are equivalent:

• $z\,$ is an $x$-intercept of $\,R$
• $N(z) = 0\,$ and $\,D(z) \ne 0$
• $R(z) = 0$
• $z\,$ is a zero of $\,R$
• $z\,$ is a root of $\,R$
• $N(x)\,$ has a factor of $\,x - z\,,$ and $D(x)$ does not have a factor of $\,x - z$

Example

Find the $x$-intercept(s) of $\,\displaystyle f(x) = \frac{x^2 - 1}{2x - 3}\,.$

Solution

Notice that $\,x = -1\,$ and $\,x = 1\,$ are both in the domain of $\,f\,.$ The graph crosses the $x$-axis at $\,x = -1\,$ and $\,x = 1\,.$