Introduction to Functions
Want some more advanced function concepts?
- Introduction to Function Notation
- More Practice with Function Notation
- Domain and Range of a Function
A function is a rule that takes an input, does something to it, and gives an output. Each input has exactly one output.
It is often helpful to think of a function as a box. You drop an input in the top, something happens to the input inside the box, and the output drops out the bottom.
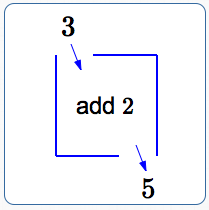
The box (the function) can be labeled with what it does. For example, if the box is labeled ‘add 2’, then when the number $\,3\,$ is dropped in the top, the number $\,3+2 = 5\,$ comes out the bottom:
$$ \cssId{s15}{\overset{\text{input}}{\overbrace{\ \ 3\ \ }}} \cssId{s16}{\overset{\text{the function adds 2}} { \overset{\text{to the input}}{\overbrace{\strut\ +\ \ 2\ }} }} \cssId{s17}{\overset{\text{and produces }}{\overbrace{\strut\ \ =\ \ }}} \cssId{s18}{\overset{\text{the output}}{\overbrace{\strut\ \ 5\ \ }}} $$