Polar Coordinates

Roughly, polar coordinates determine the position of a point in a plane
by specifying a distance from a fixed point in a given direction.

What is a Coordinate System?
‘Graph Paper’ for the Rectangular versus Polar Coordinate Systems
Definition of Polar Coordinates
Examples: Plotting Points in Polar Coordinates
Non-Uniqueness of Polar Coordinates
Simple Curves in Polar Coordinates
Converting from Polar Coordinates to Rectangular Coordinates
Converting from Rectangular Coordinates to Polar Coordinates
Flowers, Spirals, and More

What is a Coordinate System?

Pick a point in a plane. (Think of a dot on a piece of paper.)

A coordinate system is used to answer these questions:

‘Where is this point?’ or ‘How do you get to this point?’

A coordinate system always involves:

a starting place (i.e., some sort of ‘origin’)
rules for how to move from the starting place

Depending on what you're doing, one type of coordinate system might be much simpler to use than another!

As you'll see, applications involving concentric circles (circles with a common center) are probably going to be much better suited to polar coordinates (this section) than to the (more familiar and widely-used) rectangular coordinates.

radar systems
are well-suited to polar coordinates

‘Graph Paper’ for the Rectangular versus Polar Coordinate Systems

It's fun (and instructive) to compare the ways the plane is ‘divided up’ for rectangular versus polar coordinates.
A more precise discussion of polar coordinates follows.

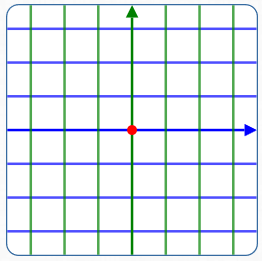
Rectangular/Cartesian/$\,xy\,$ Coordinate System

To plot a point:

start at the origin
move left/right a specified amount ($\,x\,$)
move up/down a specified amount ($\,y\,$)

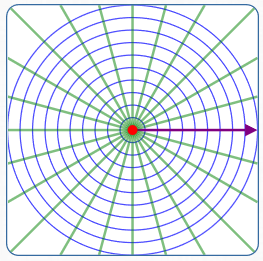
Polar Coordinate System

To plot a point:

position the starting ray;
the endpoint is called the ‘pole’
rotate the ray a specified angle ($\,\theta\,$)
move from the pole in the new direction a specified amount ($\,r\,$)

Definition of Polar Coordinates

DEFINITION polar coordinates

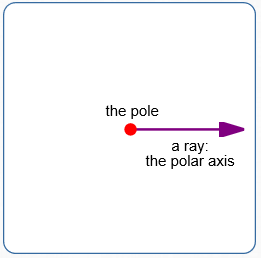
A polar coordinate system is determined by:

a plane
a ray in the plane:
- the ray is called the polar axis
- the endpoint of the ray is called the pole
Conventionally, the ray is horizontal, pointing to the right.

Let $\,r\,$ (the radius) and $\,\theta\,$ (the angle) be real numbers.
If $\,\theta\,$ has no units, then it is the radian measure of an angle.
Other units (like degrees) can also be used for $\,\theta\,.$

To determine the position of the point with polar coordinates $\,(r,\theta)\,$:

DIRECTION:
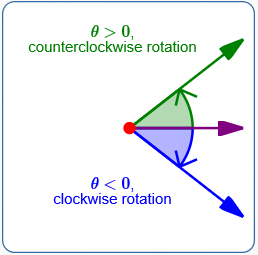
Rotate the polar axis about the pole by an amount $\,|\theta|\,$:
For $\,\theta \gt 0\,,$ rotate counterclockwise (green ray at right).
For $\,\theta = 0\,,$ there is no rotation.
For $\,\theta < 0\,,$ rotate clockwise (blue ray at right).
For convenience, call this the rotated ray.
DIRECTED DISTANCE FROM POLE:
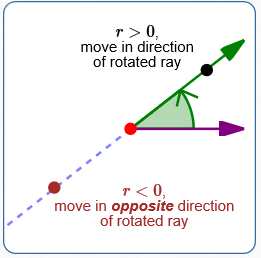
Move from the pole a distance $\,|r|\,$:
- For $\,r \gt 0\,,$ move in the direction of the rotated ray.
- For $\,r = 0\,,$ do not move.
- For $\,r \lt 0\,,$ move in the opposite direction of the rotated ray.

NOTES ON POLAR COORDINATES:

Infinitely many names for the pole:
For any angle $\,\theta\,,$ the polar coordinates $\,(0,\theta)\,$ gives the pole.
In other words, if the radius is zero, then—regardless of the angle—you get the endpoint of the polar axis.
Distinguish between rectangular and polar coordinates:
If you're using both rectangular and polar coordinates in the same discussion, then you need a way to distinguish between the two. One easy way (without introducing any new notation) is to always say something like ‘$\,(x,y) = (1,2)\,$’ versus ‘$\,(r,\theta) = (1,2)\,$’.
What does ‘$\,r = 3\,$’ really mean?
When you say something like ‘$\,r = 3\,$’ there is an implied understanding of a known unit.
That is, $\,r\,$ is $\,3\,$ WHAT? Here are two approaches you can take:
- You can agree that the polar axis ‘carries’ the units.
  In this case, the polar axis acts like (half of) a number line.
- You can agree that $\,r = 3\,$ means that $\,r\,$ is (say) $\,3\,$ centimeters.
  Of course, any unit of length can be used.

starting set-up for a
polar coordinate system

rotate the polar axis
about the pole
by an amount $\,|\theta|\,$

move the point from the pole
a distance $\,|r|\,$

Examples: Plotting Points in Polar Coordinates

In all these examples:

the polar axis is purple
the rotated ray is faded purple
the red circle has radius $\,2\,$; its center is the pole
the point with polar coordinates $\,(r,\theta)\,$ is shown in green

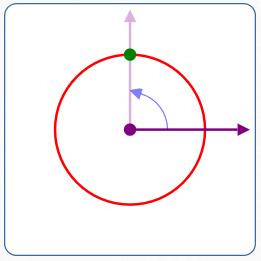
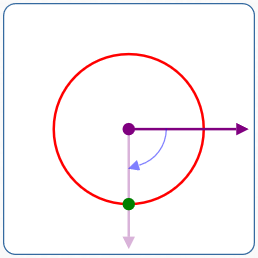
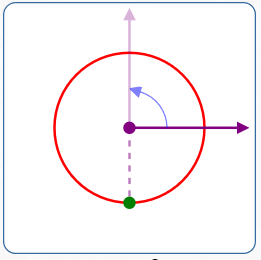
$r = 2$ $\theta = 90^\circ$ rotate the polar axis $\,90^\circ\,$ counterclockwise move $\,2\,$ units in the direction of the rotated ray	$r = 2$ $\theta = -90^\circ$ rotate the polar axis $\,90^\circ\,$ clockwise move $\,2\,$ units in the direction of the rotated ray	$r = -2$ $\theta = 90^\circ$ rotate the polar axis $\,90^\circ\,$ counterclockwise move $\,2\,$ units in the opposite direction of the rotated ray
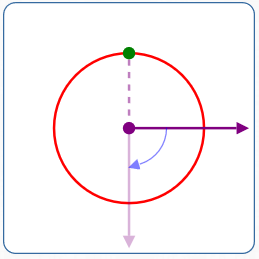
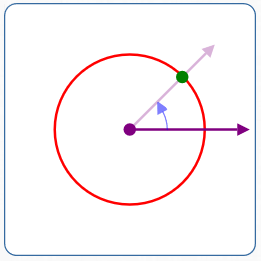
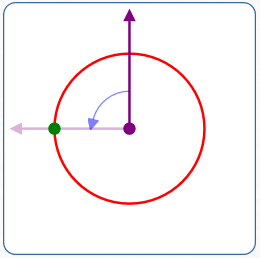
$r = -2$ $\theta = -90^\circ$ rotate the polar axis $\,90^\circ\,$ clockwise move $\,2\,$ units in the opposite direction of the rotated ray	$r = 2$ $\theta = \pi/4$ rotate the polar axis $\,\displaystyle\frac{\pi}{4}\,$ radians counterclockwise move $\,2\,$ units in the direction of the rotated ray	$r = 2$ $\theta = 90^\circ$ a different placement of the polar axis rotate the polar axis $\,90^\circ\,$ counterclockwise move $\,2\,$ units in the direction of the rotated ray

Non-Uniqueness of Polar Coordinates

In both rectangular and polar coordinates, a given coordinate pair specifies a unique point in the plane:

Rectangular coordinates: once coordinate axes are positioned, each coordinate $\,(x,y)\,$ specifies a unique point in the plane.
Polar coordinates: once the polar axis is positioned, each coordinate $\,(r,\theta)\,$ specifies a unique point in the plane.

Good thing!
You wouldn't want a coordinate pair specifying (say) one point on Monday, and a different point on Tuesday!

However, when going from a point in a plane to a coordinate pair representing it—rectangular coordinates are simpler!

Rectangular coordinates: once coordinate axes are positioned, each point in the plane corresponds to a unique pair of real numbers $\,(x,y)\,.$
For rectangular coordinates, there is a one-to-one correspondence between points in the plane and coordinate pairs $\,(x,y)\,.$
For rectangular coordinates, it is as if the points in the plane and the pairs of real numbers $\,(x,y)\,$ are tied together with strings!
Simple!
Polar coordinates: once the polar axis is positioned, each point in the plane has infinitely many coordinate pairs $\,(r,\theta)\,$ that can represent it.
Here are some examples:
- radian measure for $\,\theta\,$: $(\,r,\theta) = (r\,,\,\theta + 2\pi n)\,$ for all integers $\,n\,$
  degree measure for $\,\theta\,$: $\,(r,\theta) = (r\,,\,\theta + n\cdot 360^\circ)\,$ for all integers $\,n\,$
  If you sweep the angle one or more complete revolutions in either direction, you get to the same place!
- radian measure for $\,\theta\,$: $\,(r,\theta) = \bigl(-r\,,\,\theta + (2n+1)\pi\bigr)\,$ for all integers $\,n\,$
  degree measure for $\,\theta\,$: $\,(r,\theta) = \bigl(-r\,,\,\theta + (2n+1)\cdot 180^\circ\bigr)\,$ for all integers $\,n\,$
  Sweep to ‘opposite’ the desired point, then go backwards!
For polar coordinates, it is as if each point in the plane has infinitely many strings coming from it, each going to a different polar coordinate representation for the point. Depending on the application, this may or may not be desirable.

There are different ways that you can restrict $\,r\,$ and $\,\theta\,$ to get a unique representation for each point in polar coordinates.
Here are two of the most common ways:

radian measure for $\,\theta\,$: require $\,r\ge 0\,,$ $\,0 \le \theta < 2\pi\,,$ and represent the pole by only $\,(0,0)\,$
radian measure for $\,\theta\,$: require $\,r\ge 0\,,$ $\,-\pi \lt \theta \le \pi\,,$ and represent the pole by only $\,(0,0)\,$

There are corresponding restrictions for degree measure.
Note that unless you specify a unique representation for the pole, it would have ‘names’ $\,(0,\theta)\,$ for all possible values of $\,\theta\,.$

READ-THROUGH, PART 2

Simple Curves in Polar Coordinates

Different coordinate systems make different curves extremely easy to plot:

rectangular coordinate system:
- vertical lines: $\,x = \text{some #}\,$
- horizontal lines: $\,y = \text{some #}\,$
polar coordinate system:
- circles centered at the pole: $\,r = \text{some #}\,$
- lines through the pole: $\,\theta = \text{some #}\,$

GRAPH	EQUATION/DESCRIPTION	COMMENTS
	$$\cssId{sb11}{r = 3}$$ circle with radius $\,3\,,$ centered at the pole	This is an equation in two variables: $$\cssId{sb15}{r + 0\cdot\theta = 3}\,$$ The graph is (using set-builder notation): $$\cssId{sb17}{\{\,(3,\theta) \ \ \|\ \ \theta\in\Bbb R\,\}}$$
	$$\cssId{sb18}{\theta = \frac{\pi}4}$$ or $$\cssId{sb20}{\theta = 45^\circ}$$ line through the pole	This is an equation in two variables: $$\cssId{sb23}{0\cdot r + \theta = \frac{\pi}4}\,$$ The graph is: $$\cssId{sb25}{\{\,(r,\frac{\pi}4) \ \ \|\ \ r\in\Bbb R\,\}}$$

Converting from Polar Coordinates to Rectangular Coordinates

Given a point with polar coordinates $\,(r,\theta)\,,$ we want formulas for the rectangular coordinates $\,(x,y)\,.$
That is, we want:

a formula for $\,x\,$ that depends on $\,r\,$ and $\,\theta\,$
a formula for $\,y\,$ that depends on $\,r\,$ and $\,\theta\,$

Here's the punchline:
For all real numbers $\,r\,$ and $\,\theta\,,$

$\,x = r\cos\theta\,$
$\,y = r\sin\theta\,$

The details follow.

To convert from polar to rectangular coordinates,
first introduce a rectangular coordinate system:

$x$-axis: the line through the polar axis;
positive direction is the direction of the polar axis
$y$-axis: the line through the pole, perpendicular to the $x$-axis;
positive direction corresponds to a $\,90^\circ\,$ counterclockwise rotation of the polar axis
Note that the origin of the rectangular coordinate system is the pole.

For convenience, the conventional orientations are shown at right.

NOTE:
You could position the rectangular coordinate system relative to the polar axis in many different ways. For different placements, however, the resulting formulas might be very complicated!

Use the polar axis to introduce
a rectangular coordinate system.

Plot a point in polar coordinates ($\,r \ge 0\,$) and find its rectangular coordinates:

Let $\,r\,$ and $\,\theta\,$ be real numbers, with $\,r\ge 0\,.$
(The case $\,r < 0\,$ is given below.)
The blue circle shown at right is the unit circle (radius $\,1\,$).
Consider the point with polar coordinates $\,(r,\theta)\,,$ shown at right in black.
The rotated ray is shown at right in light purple.
It does not matter how $\,\theta\,$ is ‘swept out’ to get this rotated ray!
All that matters for this discussion is the intersection of the rotated ray and the unit circle (shown in red).
Since $\,r\ge 0\,$ (by assumption), the black point $\,(r,\theta)\,$ actually lies on the rotated ray.
Note:
If $\,r > 1\,,$ then $\,(r,\theta)\,$ lies outside the unit circle (as shown at right).
If $\,r = 1\,,$ then $\,(r,\theta)\,$ lies on the unit circle.
If $\,r < 1\,,$ then $\,(r,\theta)\,$ lies inside the unit circle.
By the definition of sine and cosine, the red point has rectangular coordinates $\,(\cos\theta\,,\,\sin\theta)\,.$
Scale the coordinates of the red point by the nonnegative number $\,r\,$ to get the coordinates of the black point: $\,(r\cos\theta\,,\,r\sin\theta)\,.$

getting rectangular coordinates
for a point with polar coordinates $\,(r,\theta)\,$:
$\,r\ge 0\,$

Plot a point in polar coordinates ($\,r \lt 0\,$) and find its rectangular coordinates:

Let $\,r\,$ and $\,\theta\,$ be real numbers, with $\,r \lt 0\,.$
Everything is the same as the case above, with the minor modifications given next.
Since $\,r\lt 0\,$ (by assumption), the black point $\,(r,\theta)\,$ lies a distance $\,|r|\,$ from the pole on the opposite side of the rotated ray.
Note:
If $\,|r| > 1\,,$ then $\,(r,\theta)\,$ lies outside the unit circle (as shown at right).
If $\,|r| = 1\,,$ then $\,(r,\theta)\,$ lies on the unit circle.
If $\,|r| < 1\,,$ then $\,(r,\theta)\,$ lies inside the unit circle.
By the definition of sine and cosine, the red point has rectangular coordinates $\,(\cos\theta\,,\,\sin\theta)\,.$
Scale the coordinates of the red point by the negative number $\,r\,$ to get the coordinates of the black point: $\,(r\cos\theta\,,\,r\sin\theta)\,.$

Since the scaling number is negative, the coordinates change sign.
If an unscaled coordinate is positive, the scaled coordinate is negative.
If an unscaled coordinate is negative, the scaled coordinate is positive.

Thus, a point in Quadrant I moves to a point in Quadrant III.
A point in Quadrant II moves to a point in Quadrant IV... and so on!

getting rectangular coordinates
for a point with polar coordinates $\,(r,\theta)\,$:
$\,r\lt 0\,$

Summarizing both cases, we have:

CONVERTING FROM POLAR COORDINATES
TO RECTANGULAR COORDINATES

For all real numbers $\,r\,$ and $\,\theta\,$: $$ \cssId{sb88}{\overbrace{(r,\theta)}^{\text{polar coordinates}} \ =\ \overbrace{( \underbrace{r\cos\theta}_{\text{$x$}} \,,\, \underbrace{r\sin\theta}_{\text{$y$}} )}^{\text{rectangular coordinates}}} $$ That is:

$$ \begin{align} x &= r\cos\theta\cr y &= r\sin\theta \end{align} $$

Converting from Rectangular Coordinates to Polar Coordinates

Given a point with rectangular coordinates $\,(x,y)\,,$ we want formulas for polar coordinates $\,(r,\theta)\,.$
That is, we want:

a formula for $\,r\,$ that depends on $\,x\,$ and $\,y\,$
a formula for $\,\theta\,$ that depends on $\,x\,$ and $\,y\,$

Here's part of the punchline:
For all real numbers $\,x\,$ and $\,y\,$: $\,r = \sqrt{x^2 + y^2}\,$

Unfortunately, $\,\theta\,$ is considerably more complicated!

The details follow.

To convert from rectangular to polar coordinates, first introduce a polar axis .
The formulas are simplest by placing the pole at the origin, with the ray pointing in the direction of the positive $x$-axis.

Since every point has infinitely many names in polar coordinates,
decisions need to be made about which names to return!

Formula for $\,r\,$

As the sketch at right suggests, there's an easy formula to get a point's distance from the origin : $$\cssId{sb107}{r = \sqrt{x^2 + y^2}}$$

The table below verifies that the expression $\,\sqrt{x^2 + y^2}\,$ returns the correct distance from the origin for every point in the plane.
Recall that for all real numbers $\,t\,$:

$\,|t|\,$ gives the distance from $\,t\,$ to zero
$\sqrt{t^2} = |t|$
$\,|t|^2 = t^2\,$

point(s) $\,(x,y)\,$	distance from $\,(x,y)\,$ to origin	the expression $\,\sqrt{x^2 + y^2}\,$ gives:
the origin: $\,(0,0)\,$	$\color{red}{0}$	$\sqrt{x^2 +y^2} = \sqrt{0^2 + 0^2} = \color{red}{0}$
$x$-axis: $\,(x,0)\,$	$\color{red}{\|x\|}$	$\sqrt{x^2 +y^2} = \sqrt{x^2 + 0^2} = \sqrt{x^2} = \color{red}{\|x\|}$
$y$-axis: $\,(0,y)\,$	$\color{red}{\|y\|}$	$\sqrt{x^2 +y^2} = \sqrt{0^2 + y^2} = \sqrt{y^2} = \color{red}{\|y\|}$
four quadrants: $\,(x,y)\,$ for $\,x\ne 0\,$ and $\,y\ne 0\,$	See sketch at right: drop a perpendicular from the point to the $x$-axis the right triangle thus formed has side lengths $\,\|x\|\,$ and $\,\|y\|\,$ using the Pythagorean theorem: $$\cssId{sb131}{(\text{hyp})^2 = \|x\|^2 + \|y\|^2 = x^2 + y^2}$$ $$\cssId{sb132}{\text{hyp} = \color{red}{\sqrt{x^2 + y^2}}}$$	$\color{red}{\sqrt{x^2 + y^2}}$

Formulas for $\,\theta\,$

Using the formula $\,r = \sqrt{x^2 + y^2}\,$ guarantees that $\,r\,$ is nonnegative.
With nonnegative $\,r\,,$ there are two conventional choices for $\,\theta\,$ to get unique names for all points in the plane:

$\,0 \le \theta \lt 2\pi\,$
$\,-\pi \lt \theta \le \pi\,$

Quadrant I (where $\,x > 0\,$ and $\,y > 0\,$) is no problem!

Given a point $\,(x,y)\,$ in Quadrant I, the right triangle shown at right always has these properties:

For polar coordinates, we need $\,\color{red}{\theta}\,.$
The side OPPosite $\,\color{red}{\theta}\,$ has length $\,y\,.$
The side ADJacent to $\,\color{red}{\theta}\,$ has length $\,x\,.$
Thus, $\displaystyle\,\color{red}{\tan \theta = \frac{\text{OPP}}{\text{ADJ}} = \frac yx}\,.$

In Quadrant I, $\,\color{red}{\theta}\,$ is always between $\,0\,$ and $\,\frac\pi 2\,.$
So, we want the angle between $\,0\,$ and $\,\frac\pi 2\,$ whose tangent is $\,\frac yx\,.$
In this case, the arctangent gives us precisely the angle we want! $$ \cssId{sb149}{\color{red}{\theta \ = \ \arctan \frac yx \ = \ \overbrace{\tan^{-1}\frac yx}^{\text{alternate notation}}}} $$ Since (by definition) the arctangent function always returns angles in the interval $\,(-\frac{\pi}2\,,\,\frac{\pi}2)\,,$
once we leave Quadrant I, the formulas for $\,\theta\,$ may require some ‘tweaking’.

As you'll see next, the formula for $\,\theta\,$ is a piecewise-defined function—with quite a few pieces!

Quadrant I: $\,x > 0\,$ and $\,y > 0\,$

In this quadrant:
$\displaystyle\theta = \arctan \frac yx$

Piecewise-defined function that returns $\,\theta\in [0,2\pi)\,$ for points $\,(x,y)\,$:

These sketches are used to get the different ‘pieces’ for the piecewise-defined function.
In all sketches, the black point has rectangular coordinates $\,(x,y)\,.$

$\,x \gt 0\,$ and $\,y\ge 0\,$ Here: $\displaystyle\,\frac yx \ge 0\,$ $\displaystyle\,\color{red}{\theta = \arctan{\frac yx}}\,$ Note: $\displaystyle\,\theta\in [0,\frac\pi 2)\,$ Note: when $\,y = 0\,,$ $\,\theta = \arctan{\frac yx} = \arctan 0 = 0\,$	$\,x = 0\,$ and $\,y\gt 0\,$ Here: $\displaystyle\,\frac yx\,$ is not defined $\displaystyle\,\color{red}{\theta = \frac\pi 2}\,$	$\,x \lt 0\,$ and $\,y\ge 0\,$ Here: $\displaystyle\,\frac yx \le 0\,$ $\displaystyle\,\color{red}{\theta = (\arctan{\frac yx}) + \pi}\,$ Note: $\displaystyle\,\theta\in (\frac\pi 2,\pi]\,$ Note: when $\,y = 0\,,$ $\,\theta = (\arctan{\frac yx}) + \pi = (\arctan 0) + \pi = \pi\,$	$\,x \lt 0\,$ and $\,y\lt 0\,$ Here: $\displaystyle\,\frac yx \gt 0\,$ $\displaystyle\,\color{red}{\theta = (\arctan{\frac yx}) + \pi}\,$ Note: $\displaystyle\,\theta\in (\pi,\frac{3\pi}2)\,$
$\,x = 0\,$ and $\,y\lt 0\,$ Here: $\displaystyle\,\frac yx\,$ is not defined $\displaystyle\,\color{red}{\theta = \frac{3\pi}{2}}\,$	$\,x \gt 0\,$ and $\,y\lt 0\,$ Here: $\displaystyle\,\frac yx \lt 0\,$ $\displaystyle\,\color{red}{\theta = (\arctan{\frac yx}) + 2\pi}\,$ Note: $\displaystyle\,\theta\in (\frac{3\pi}2,2\pi)\,$	$\,x = 0\,$ and $\,y = 0\,$ Here: $\displaystyle\,\frac yx\,$ is not defined $\displaystyle\,\color{red}{\theta = 0}\,$ Note: For uniqueness, we can agree that the point with rectangular coordinates $\,(0,0)\,$ gets represented only by $\,r = 0\,$ and $\,\theta = 0\,.$	The piecewise-defined description of $\,\theta\,$ is given below. Similarly, you can find formulas for $\,\theta\,$ when the desired angles to be returned are in the interval $\,(-\pi,\pi]\,.$

This formula for $\,\theta\,,$
together with $\,r = \sqrt{x^2 + y^2}\,,$
gives a unique representation $\,(r,\theta)\,$
for each point with rectangular coordinates $\,(x,y)\,.$

The angles $\,\theta\,$ are in the interval $\,[0,2\pi)\,.$

$$ \cssId{sb202}{\theta = \cases{\cr 0 &if $\,x = 0\,$ and $\,y = 0\,$\cr\cr \arctan\frac yx &if $\,x \gt 0\,$ and $\,y \ge 0\,$\cr\cr \frac\pi 2 &if $\,x = 0\,$ and $\,y \gt 0\,$\cr\cr \pi +\arctan\frac yx &of $\,x \lt 0\,$\cr\cr \frac{3\pi} 2 &if $\,x = 0\,$ and $\,y \lt 0\,$\cr\cr 2\pi +\arctan\frac yx &if $\,x \gt 0\,$ and $\,y \lt 0\,$ }} $$

Flowers, Spirals, and More

There are many fun/interesting/beautiful curves that can be described by simple equations involving $\,r\,$ and $\,\theta\,.$
These are sometimes called ‘polar curves’.

SPIRALS (and more)

At right, $\,r\,$ is a simple linear function of $\,\theta\,$: $$\cssId{sb208}{r = m\theta + b\,, \qquad \text{ for } \theta\in [\theta_{\text{start}},\theta_{\text{end}}]}$$ Change parameters by setting values and clicking the ‘Plot the curve!’ button.

Three points are given:

The blue point is the start point: $\,r_\text{start} := m\theta_{\text{start}} + b\,$
The green point is the end point: $\,r_\text{end} := m\theta_{\text{end}} + b\,$
The red point is a glider on the curve.
Drag it around!
Rectangular coordinates are ‘attached to’ the point.
Corresponding polar coordinates are displayed at the top right of the graph (with $\,\theta\,$ between $\,-180^\circ\,$ and $\,180^\circ\,$).

Note that:

$\,m\,$ controls how fast $\,r\,$ changes:
When $\,\theta\,$ changes by an amount $\,\Delta\theta\,,$ then $\,r\,$ changes by $\,m\Delta\theta\,.$
That is, $\,r\,$ changes $\,m\,$ times faster than $\,\theta\,.$
$\,b\,$ gives an ‘offset’:
When $\,\theta = 0\,,$ then $\,r = m(0) + b = b\,.$
The viewing screen changes as needed, so that you can see the entire curve. If you change a value and it looks like the graph hasn't changed—check the scales on the $x$ and $y$ axes!

Type in desired values for the curve $\,r = m\theta + b\,$:
$\,m\,$:	$\,b\,$:	$\,\theta_{\text{start}}\,$ (radians):	$\,\theta_{\text{end}}\,$ (radians):

$r = m\theta + b$, for $\, \theta\in [\theta_{\text{start}},\theta_{\text{end}}]$

Here are some for you to try:


$r = \theta\,,$ for $\,\theta\in [0,4\pi]$	$r = -\theta\,,$ for $\,\theta\in [0,2\pi]$	$r = 3\theta - 10\,,$ for $\,\theta\in [0,5\pi]$	$r = 0.3\,\theta\,,$ for $\,\theta\in [-10,10]$

FLOWERS (and more)

Of course, WolframAlpha can plot polar curves!
Here are some for you to try—you can cut-and-paste the text below each image (if desired).

Polar Rose: $r = a\cos(k\theta)\,$ $a$ gives the length of the petals		Just have fun!
Gives a rose with $\,k\,$ petals when $\,k\,$ is an odd integer (for $\,\theta\in [0,\pi]\,$)	Gives a rose with $\,2k\,$ petals when $\,k\,$ is an even integer (for $\,\theta\in [0,2\pi]\,$)	Just have fun!

`r = 2cos(5theta), with theta from 0 to pi`	`r = 3cos(4theta), with theta from 0 to 2pi`	`r = 10 + sin(2pitheta), for theta from 0 to 14pi`	`r = theta * cos(theta), for theta from -4pi to 4pi`
You can cut-and-paste the text above into WolframAlpha, and then play around!

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Parametric Equations