 More on Difference Quotients
More on Difference Quotients
Difference quotients were introduced in an earlier lesson: Prerequisites: Function Review; Difference Quotients.
Evaluating difference quotients requires a high degree of comfort working with functions and function notation, and this earlier lesson offers a thorough review.
Then, this current lesson gives practice with difference quotient problems involving reciprocal functions and square roots.
Let $\,f\,$ be a function and let $\,h\,$ be a nonzero number.
A difference quotient is an expression of the form $$\cssId{s9}{\frac{f(x+h)-f(x)}h}\ ,$$ which is a simplified version of: $$\cssId{s11}{\frac{f(x+h)-f(x)}{(x+h)-x}}$$
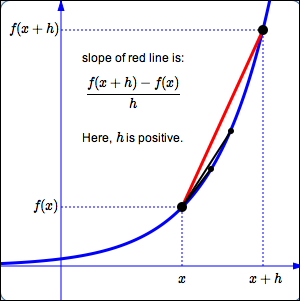
This expression gives the slope of the line through the points:
$(x\,,\,f(x))$
and
$(x+h\,,\,f(x+h))$
Since the expression is a quotient (division) of differences (subtractions), the name difference quotient is appropriate.
Comments on Difference Quotients
- If $\,h\,$ is positive, then $\,x+h\,$ lies to the right of $\,x\,$ (see sketch above).
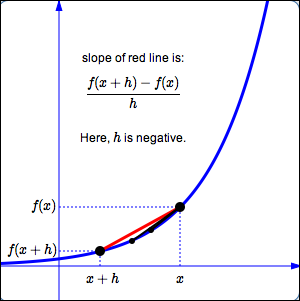
- If $\,h\,$ is negative, then $\,x+h\,$ lies to the left of $\,x\,$ (see sketch below).
- If $\,h\,$ is zero, then the point $\,(x+h,f(x+h))\,$ degenerates to the original point $\,(x,f(x))\,.$ There is not a unique line through a single point. The difference quotient is not defined when $\,h = 0\,$ (division by zero).
- As $\,h\,$ gets close to zero, $\,x+h\,$ gets close to $\,x\,.$
- When $\,h\,$ is small, the point $\,(x+h,f(x+h))\,$ is likely to be close to the point $\,(x,f(x))\,.$ (The two tiny black points in the sketches above are for smaller values of $\,h\,.$)
- The sketches above show what can happen as $\,h\,$ approaches zero: here, the line between $\,(x,f(x))\,$ and the successively closer points $\,(x+h,f(x+h))\,$ is looking more and more like the tangent line to the graph of $\,f\,$ at $\,x\,.$
-
(Calculus preview): In Calculus, you will firm up the concept of limit. Sometimes limits exist, and sometimes they don't.
When the following limit exists, then it gives the slope of the tangent line to the graph of $\,f\,$ at the point $\,(x,f(x))\,$:
$$ \cssId{s33}{\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}h} $$Read as: the limit, as $\,h\,$ approaches zero, of ...
To evaluate this limit, you need to rename the difference quotient to get ‘$\,h\,$’ out of the denominator. With the new name, you'll then be able to understand what happens as $\,h\,$ gets close to zero.
The process of ‘getting $\,h\,$ out of the denominator’ often requires considerable algebraic manipulation—you'll get practice in this section!
Example: A Difference Quotient for the Reciprocal Function
Let $\displaystyle\,f(x) = \frac 1x\,.$
Find the difference quotient $\ \frac{f(x+h)-f(x)}h\ ,$ and write it in a form with no $\,h\,$ in the denominator.
What does the difference quotient approach, as $\,h\,$ approaches zero? What is the significance of this result?
| $\displaystyle\frac{f(x+h)-f(x)}h$ | The desired difference quotient |
| $\displaystyle = \frac{\frac 1{x+h} - \frac 1x}h$ | Function evaluation; use definition of $\,f\,$ |
| $\displaystyle = \frac{\frac 1{x+h}\cdot\frac xx - \frac 1x\cdot\frac{x+h}{x+h}}h$ | Get a common denominator |
| $\displaystyle = \frac{\frac x{x(x+h)} - \frac {x+h}{x(x+h)}}h$ | Simplify |
| $\displaystyle = \frac{\frac {x - (x+h)}{x(x+h)}}h$ | Write the numerator as a single fraction |
| $\displaystyle = {\frac {x-x-h}{x(x+h)}}\cdot\frac 1h$ | Distributive law; and, dividing by $\,h\,$ is the same as multiplying by $\,\frac 1h\,$ |
| $\displaystyle = {\frac {-h}{x(x+h)h}}$ | $x - x = 0\,$; and multiply across |
| $\displaystyle = {\frac {-1}{x(x+h)}}$ |
Cancel: since $\,h\ne 0\,,$
$\,\frac hh = 1\,.$
Now, the factor of $\,h\,$ is gone in the denominator! |
As $\,h\,$ approaches zero, $\, {\frac {-1}{x(x+h)}}\,$ approaches $\,\frac{-1}{x(x+0)}\,,$ which equals $\, -\frac 1{x^2}\,.$
The formula $\,-\frac{1}{x^2}\,$ gives the slopes of the tangent lines to the graph of $\,f(x) = \frac 1x\,$!
For example, the slope of the tangent line to $\,f(x) = \frac 1x\,$ at the point $\,(3,\frac 13)\,$ is $\,-\frac{1}{3^2} = -\frac 19\,.$
Click ‘Submit’ on the WolframAlpha widget below to explore the power of Wolfram Alpha! You can create your own widgets by clicking here.
Step-by-Step Guided Practice
- Click ‘New Problem’ to get started.
- Want a hint for each step? Click the ‘Hint?’ button.
- When you're ready to check your answer, click the ‘Show’ button.
| To get a new problem, click the ‘New Problem’ button at left! | ||
| HINTS: | ||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
Back to the top to try another problem!