• Jump right to the exercises!
• Want some basic practice first?
  Introduction to the Slope of a Line

In a rush? Need to skip the concepts and jump right to the slope formula?
(Please come back and explore the beautiful ideas at a later time.)

Consider the equation [beautiful math coming... please be patient] $\,y = mx + b\,$.
As we'll see in this section, every equation of this form graphs as a non-vertical line in the coordinate plane.

In this equation, [beautiful math coming... please be patient] $\,m\,$ is the coefficient of the $\,x$-term, and $\,b\,$ is a constant term.
For example, in the equation [beautiful math coming... please be patient] $\,y = 2x + 3\,$, we have $\,m = 2\,$ and $\,b = 3\,$.

The number $\,m\,$ is called the slope of the line, and gives information about the ‘slant’ of the line.
It answers questions like:   “Is it an uphill or downhill line?   How steep is it?”
The purpose of this section is to explain why this is true.

The key idea (which we'll prove below) is that the equation [beautiful math coming... please be patient] $\,y = mx + b\,$ defines a very special relationship between $\,x\,$ and $\,y\,$: equal changes in $\,x\,$ (the input) give rise to equal changes in $\,y\,$ (the output). Indeed, if $\,x\,$ changes by an amount [beautiful math coming... please be patient] $\,\Delta x\,$ (read aloud as ‘delta ex’ or ‘change in ex’), then $\,y\,$ changes by $\,m\Delta x\,$. That is, $\,y\,$ changes $\,m\,$ times as fast as $\,x\,$. This is a bit symbol-intensive, so let's look at a concrete example. Suppose that [beautiful math coming... please be patient] $\,m\,$ is $\,2\,$. (See the sketch at right.) Then, $\,y\,$ changes $\,2\,$ times as fast as $\,x\,$ (that is, twice as fast as $\,x\,$). If (say) $\,x\,$ changes by $\,1\,$, then $\,y\,$ will change by $\,2(1) = 2\,$. If (say) $\,x\,$ changes by $\,5\,$, then $\,y\,$ will change by $\,2(5) = 10\,$, and so on. 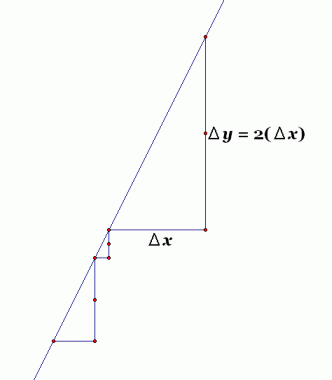Here's another way to look at it. Imagine you're ‘standing on’ a point in the coordinate plane. Let's force [beautiful math coming... please be patient] $\,y\,$ to change twice as fast as $\,x\,$, and see what new points result: If you take $\,1\,$ step to the right (i.e., let $\,x\,$ change by $\,1\,$), then you'll have to take $\,2\,$ steps up (i.e., let $\,y\,$ change by $\,2\,$). Do it again—one step to the right, two steps up. Do it again—one step to the right, two steps up. (Repeat, if you want, with different changes in $\,x\,$.) Hmmm$\,\ldots\,$ what pattern are these points creating? A line!! If we repeat the previous exercise with $\,m=100\,$, think about the line that would result: one step to the right, $\,100\,$ steps up. Pretty steep line! So, clearly, the number $\,m\,$ gives information about the steepness or ‘slant’ of the line.

The next part is a bit technical, so perhaps a break is in order first.
You can get some Fun Facts about the site creator and support this site.

Let [beautiful math coming... please be patient] $\,(x_1,y_1)\,$ be a point on the graph of $\,y = mx + b\,$, so that $\,y_1 = mx_1 + b\,$.
That is, when you substitute $\,x_1\,$ for $\,x\,$ and $\,y_1\,$ for $\,y\,$, the resulting equation is true.

Let [beautiful math coming... please be patient] $\,x_1\,$ change by an amount $\,\Delta x\,$, to get a new $\,x\,$-value:   $\,x_2 = x_1 + \Delta x\,$

Let $\,y_2\,$ represent the $\,y$-value corresponding to $\,x_2\,$.
Then,

Make sure you see this!

Let's summarize things from the previous proof.
We started at [beautiful math coming... please be patient] $\,(x_1,y_1)\,$.
We ended at $\,(x_2,y_2)\,$.

The change in $\,x\,$ is:   $\,\Delta x = x_2 - x_1\,$
A ‘change in $\,x\,$’ is informally called a run, since it is in the left/right direction.
Memory device:   Run to the right! Run to the left!

The change in $\,y\,$ is:   $\,\Delta y = y_2 - y_1\,$
A ‘change in $\,y\,$’ is informally called a rise, since it is in the up/down direction.
Memory device:   Rise up!

And, we learned that the change in $\,y\,$ is $\,m\Delta x\,$:   in equation form, [beautiful math coming... please be patient] $\,\Delta y = m\Delta x\,$.
Solving this last equation for the slope, $\,m\,$, gives us an important formula:

There are lots of important things you should know about the slope formula:

• HOW TO USE THE SLOPE FORMULA:
  To find the slope of a non-vertical line, you can choose any two different points on the line.
  Take the difference of the $\,y$-values. This is your ‘rise’.
  Take the difference of the $\,x$-values. This is your ‘run’.
  Divide rise by run, and you've got your slope!
• BE CAREFUL—ORDER IS IMPORTANT!
  Once you do your first subtraction, the next subtraction must be done in the same order.
  For example, suppose your two points are $\,(1,5)\,$ and $\,(3,12)\,$.
  If you say [beautiful math coming... please be patient] $\,\Delta x = 3-1=2\,$, then you must say $\,\Delta y = 12-5 = 7\,$, and $\,m = \frac{7}{2}\,$.
  Or:
  If you say $\,\Delta x = 1-3=-2\,$, then you must say $\,\Delta y = 5-12 = -7\,$, and $\,m = \frac{-7}{-2} = \frac 72\,$.
  Either way is fine.
  But DON'T use (say) $\,3-1\,$ for one and $\,5-12\,$ for the other!
• RUN:
  If the change in [beautiful math coming... please be patient] $\,x\,$ is $\,2\,$, you go to the right two.
  If the change in $\,x\,$ is $\,-2\,$, you go to the left two.
  ‘Run’ is positive to the right, and negative to the left.
• RISE:
  If the change in [beautiful math coming... please be patient] $\,y\,$ is $\,2\,$, you go up two.
  If the change in $\,y\,$ is $\,-2\,$, you go down two.
  ‘Rise’ is positive UP, and negative DOWN.
• HORIZONTAL LINES:
  Since two points on a horizontal line have the same $\,y$-value,
  [beautiful math coming... please be patient] $\,\text{slope} = \frac{y_2-y_1}{x_2-x_1} = \frac{0}{x_2-x_1} = 0\,$.
  The slope of a horizontal line is zero.
• VERTICAL LINES:
  Since two points on a vertical line have the same $\,x$-value,
  an attempt to compute the slope fails:
  $\,\text{slope} = \frac{y_2-y_1}{x_2-x_1} = \frac{y_2-y_1}{0} = \text{Can't continue!}$
  Division by zero is not allowed.
  Thus, you can't compute the slope of a vertical line.
  We say that vertical lines have NO slope.
• ZERO SLOPE versus NO SLOPE:
  Note that ‘zero slope’ and ‘no slope’ mean two entirely different things!
  Horizontal lines have zero slope; vertical lines have no slope.

horizontal line, zero slope	vertical line, no slope

• UPHILL LINES, POSITIVE SLOPE:
  Imagine you're standing on a line in the coordinate plane, walking from left to right.
  If you're going uphill, then we'll informally call this an ‘uphill line’.
  On uphill lines, if you rise-and-run from point-to-point, one of two situations occur:
  
  • rise and run are both positive, so $\text{slope} = \frac{+}{+} = \text{positive}$
  • rise and run are both negative, so $\text{slope} = \frac{-}{-} = \text{positive}$
  Thus, uphill lines have positive slopes.
  

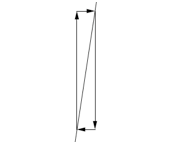
UPHILL LINES, POSITIVE SLOPES gradual uphill, small positive slope steep uphill, large positive slope

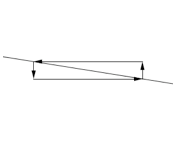
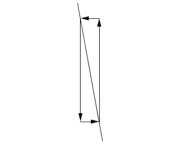
DOWNHILL LINES, NEGATIVE SLOPES gradual downhill, small negative slope steep downhill, large negative slope

• DOWNHILL LINES, NEGATIVE SLOPE:
  Imagine you're standing on a line in the coordinate plane, walking from left to right.
  If you're going downhill, then we'll informally call this a ‘downhill line’.
  On downhill lines, if you rise-and-run from point-to-point, one of two situations occur:
  
  • rise is positive and run is negative, so $\text{slope} = \frac{+}{-} = \text{negative}$
  • rise is negative and run is positive, so $\text{slope} = \frac{-}{+} = \text{negative}$
  Thus, downhill lines have negative slopes.