Introduction to Limits

Let $\,f\,$ be a function: $\,f\,$ takes inputs, does something to them, and gives corresponding outputs.

For example, $\,f\,$ might take the input $\,2\,$ and give the corresponding output $\,f(2)\,.$

Remember: $\,f(2)\,$ represents the output from the function $\,f\,$ when the input is $\,2\,.$

Perhaps, however, the function $\,f\,$ has become damaged. Oh dear! It is no longer able to act on the input $\,2\,$! Then, we might find ourselves asking the following question:

When the inputs are close to $\,2\,$ (but not equal to $\,2\,$), then what's happening to the corresponding outputs?

This scenario of letting inputs get close to a given number (but never actually getting there), and exploring the corresponding outputs, leads to the calculus concept of a limit.

Every important calculus idea relies on the idea of a limit! The idea of a limit is the central idea in calculus! The purpose of this section is to begin to explore—mostly at an intuitive level—the idea of limits.

A First Example: Inputs Close to $\,2\,$, Outputs Close to $\,4$

Consider the three sketches below:

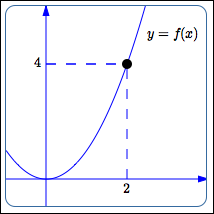
In this first sketch, the function is defined at $\,2\,$ in a ‘normal’ way.

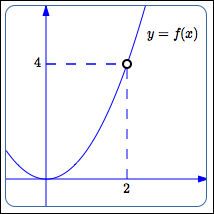
In the second sketch, the function isn't defined at $\,2\,$ at all.

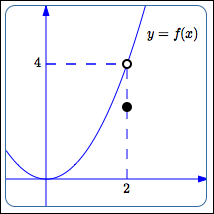
In the third sketch, the function is defined at $\,2\,$ in an unusual way.

However, in all three cases the behavior is the same:

When the inputs are close to $\,2\,$ (but not equal to $\,2\,$), the corresponding outputs are close to $\,4\,.$

So, how will this behavior be described, using mathematical notation?

Answer: in two different (equivalent) ways:

$\displaystyle {\lim_{x\rightarrow 2} f(x)} = 4$

Read as: ‘ the limit of $\,f\,$ of $\,x\,,$ as $\,x\,$ approaches $\,2\,,$ equals $\,4\,$’
as $x\rightarrow 2$, $f(x) \rightarrow 4$

Read as: ‘as $\,x\,$ approaches $\,2\,,$ $\,f\,$ of $\,x\,$ approaches $\,4\,$’

Here's a key idea: It doesn't matter what's happening at $\,2\,$! When we investigate a limit as $\,x\,$ approaches $\,2\,,$ we never let $\,x\,$ equal $\,2\,.$ We only let $x$ get arbitrarily close to $\,2\,.$

LIMITS (intuitive) the limit of $f(x)$, as $x$ approaches $c$, equals $\ell$

Consider the mathematical sentence:

$$\lim_{x\rightarrow c} f(x) = \ell$$

This sentence is read aloud as:

‘ the limit of $\,f\,$ of $\,x\,,$ as $\,x\,$ approaches $\,c\,,$ equals $\,\ell\,$’

The sentence can alternatively be written as

$$\text{as } x\rightarrow c,\ \ f(x) \rightarrow \ell$$

in which case it is read aloud as:

‘as $\,x\,$ approaches $\,c\,,$ $\,f\,$ of $\,x\,$ approaches $\,\ell\,$’

Under what conditions is this sentence true?

(Least precise)
As the inputs get close to $\,c\,,$ the corresponding outputs from $\,f\,$ get close to $\,\ell\,.$
(More precise)
We can get the outputs from $\,f\,$ as close to $\,\ell\,$ as desired, by requiring that the inputs be sufficiently close to $\,c\,$ (but not equal to $\,c\,$).
(Most precise; the definition)
For every $\,\epsilon \gt 0\,,$ there exists $\,\delta \gt 0\,,$ such that if $\,x\in \text{dom}(f)\,$ and $\,0 \lt |x - c| \lt \delta\,,$ then $\,|f(x) - \ell| \lt \epsilon\,.$

For now, don't worry about that scary-looking definition—a time will come when it will make sense!

Observations About Limits

Two-Sided Limit

Suppose the function $\,f\,$ is defined on both sides of $\,c\,.$ Then, when you investigate the limit as the inputs approach $\,c\,,$ you must approach $\,c\,$ from both sides—that is, from the left, and from the right.

In order for the limit to exist, the outputs must approach the same number coming in from both sides.

For this reason, $\ \displaystyle\lim_{x\rightarrow c} f(x)\ $ is often called a ‘two-sided limit’.

A Limit May Not Exist

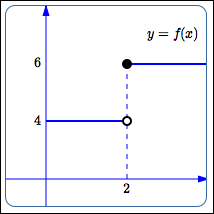
In the sketch above:

As $\,x\,$ approaches $\,2\,$ from the right, the outputs approach $\,6\,.$ (In this simple example, they're actually all equal to $\,6\,$!)
As $\,x\,$ approaches $\,2\,$ from the left, the outputs approach $\,4\,.$ (In this simple example, they're actually all equal to $\,4\,$!)

Since we get different numbers coming in from different sides, the limit does not exist (abbreviated by ‘ DNE ’).

Existence of a Limit

If there exists any number $\,\ell\,$ for which the sentence $\ \displaystyle\lim_{x\rightarrow c} f(x) = \ell\ $ is true, then we say that the ‘$\,\displaystyle\lim_{x\rightarrow c} f(x)\,$ exists ’.

So, what does it mean when we say that the ‘$\displaystyle\lim_{x\rightarrow c} f(x)$ exists’ ? It means that as the inputs approach $\,c\,,$ the corresponding outputs are approaching something.

A Limit (When it Exists) is a Number

A limit (when it exists) is a number; it is a mathematical expression.

So, what exactly is the number $\,\displaystyle\lim_{x\rightarrow c} f(x)\,$? It is the number that the outputs from $\,f\,$ are approaching, as the inputs approach $\,c\,.$

Dummy Variables in Limits

When working with limits, we need a variable to represent the inputs, so that we can talk about the corresponding outputs.

The choice of variable to represent the input is largely up to us. Thus, we can write

$$ \begin{gather} \lim_{\boldsymbol{x}\rightarrow 2}\, f(\boldsymbol{x})\cr\cr \text{ or }\cr\cr \lim_{\boldsymbol{t}\rightarrow 2}\, f(\boldsymbol{t})\cr\cr \text{ or }\cr\cr \lim_{\boldsymbol{s}\rightarrow 2}\, f(\boldsymbol{s})\cr\cr \text{ or }\cr\cr \lim_{\boldsymbol{u}\rightarrow 2}\, f(\boldsymbol{u})\cr\cr \text{ or } \ldots \end{gather} $$

Two of the most common symbols to represent inputs are $\,x\,$ and $\,t\,.$ The variable chosen to represent the input is called a dummy variable.