 Exponential Functions: Review and Additional Properties
Exponential Functions: Review and Additional Properties
An exponential function is a function of the form $\,f(x) = b^x\,$ for $\,b \gt 0\,$ and $\,b\ne 1\,.$
Notice that the variable is in the exponent. For example, $\,y = 2^x\,,$ $\,y = (\frac 12)^x\,,$ and $\,y = \text{e}^x\,$ are exponential functions.
Exponential functions and their graphs were introduced in the Algebra II curriculum:
- Thoroughly study this earlier section: Introduction to Exponential Functions
- Print out a 20-question worksheet to make sure you've mastered all the different problem types.
Additional higher-level information that is important for Precalculus is presented below.
Increasing/Decreasing Properties of Exponential Functions
Increasing Exponential Functions
When $\,b \gt 1\,,$ $\,f(x) = b^x\,$ is an increasing function. That is, for all real numbers $\,x\,$ and $\,y\,$:
$$ \cssId{s13}{x \lt y} \ \ \cssId{s14}{\Rightarrow}\ \ \cssId{s15}{b^x \lt b^y} $$It is clear from the graph (below) that the other direction is also true:
$$ \cssId{s17}{b^x \lt b^y} \ \ \cssId{s18}{\Rightarrow}\ \ \cssId{s19}{x \lt y} $$Together, we have:
$$ \cssId{s21}{x \lt y}\ \ \cssId{s22}{\text{is equivalent to}}\ \ \cssId{s23}{b^x \lt b^y} \tag{1} $$Notice that when the base is greater than one, the inequality symbols that compare the inputs ($\,x\,$ and $\,y\,$) and their corresponding outputs ($\,b^x\,$ and $\,b^y\,$) have the same direction:
$$ \cssId{s26}{x \ {\bf\color{red}{\lt }}\ y}\ \ \cssId{s27}{\text{is equivalent to}}\ \ \cssId{s28}{b^x\ {\bf\color{red}{\lt }}\ b^y} \tag{1a} $$This equivalence can be alternatively stated as:
$$ \cssId{s30}{x \ {\bf\color{red}{>}}\ y}\ \ \cssId{s31}{\text{is equivalent to}}\ \ \cssId{s32}{b^x\ {\bf\color{red}{>}}\ b^y} \tag{1b} $$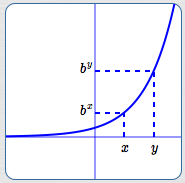
$y = b^x\,,$ for $\,b \gt 1\,$
An Increasing
Exponential Function
$x \lt y \ \ \iff\ \ b^x \lt b^y$
Decreasing Exponential Functions
When $\,0 \lt b \lt 1\,,$ $\,f(x) = b^x\,$ is a decreasing function. That is, for all real numbers $\,x\,$ and $\,y\,$:
$$ \cssId{s39}{x \lt y \ \ \Rightarrow\ \ b^x \gt b^y} $$It is clear from the graph (below) that the other direction is also true:
$$ \cssId{s41}{b^x \gt b^y \ \ \Rightarrow\ \ x \lt y} $$Together, we have:
$$ \cssId{s43}{x \lt y\ \ \text{is equivalent to}\ \ b^x \gt b^y} \tag{2} $$Notice that when the base is between zero and one, the inequality symbols that compare the inputs ($\,x\,$ and $\,y\,$) and their corresponding outputs ($\,b^x\,$ and $\,b^y\,$) have different directions:
$$ \cssId{s46}{x \ {\bf\color{red}{\lt}}\ y\ \ \text{is equivalent to}\ \ b^x\ {\bf\color{red}{\gt}}\ b^y} \tag{2a} $$This equivalence can be alternatively stated as:
$$ \cssId{s48}{x \ {\bf\color{red}{\gt}}\ y\ \ \text{is equivalent to}\ \ b^x\ {\bf\color{red}{\lt}}\ b^y} \tag{2b} $$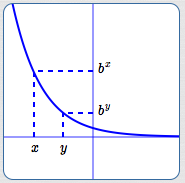
$y = b^x\,,$ for
$\,0 \lt b \lt 1\,$
A Decreasing
Exponential Function
$x \lt y \ \ \iff\ \ b^x \gt b^y$
Exponential Functions are One-to-One
The graphs of exponential functions pass both vertical and horizontal lines tests, so they are one-to-one functions. Thus:
$$ \cssId{s56}{x = y \ \ \text{is equivalent to}\ \ b^x = b^y} \tag{3}$$Consequently, exponential functions have inverses. In a future section, we'll see that the class of logarithmic functions provide inverses to the class of exponential functions.
Solving Inequalities Involving Exponential Functions
Equivalences (1), (2), and (3) can be used to easily solve certain types of mathematical sentences, as illustrated in the following examples.
Example 1
Solve: $2^{3x-1} \lt 2^{5x}$
This is an inequality of the form
$$ \cssId{s64}{b^{\text{stuff1}} \lt b^{\text{stuff2}}} $$where the base, $\,b\,,$ is $\,2\,.$ Notice that the exponential functions on both sides use the same base.
In this example, the base is greater than one, so we'll use equivalence (1):
$$ \cssId{s68}{x \lt y \ \ \iff\ \ b^x \lt b^y} $$Solution:
$$\begin{align} &\cssId{s70}{2^{3x-1}}\cssId{s71}{\lt} \ \cssId{s72}{2^{5x}}\cr &\quad\cssId{s73}{\text{original inequality}}\cr\cr &\cssId{s74}{3x-1}\cssId{s75}{\lt} \cssId{s76}{5x}\cr &\quad\cssId{s77}{\text{use (1); inequality symbol doesn't change}}\cr\cr &\cssId{s78}{-2x}\cssId{s79}{\lt} \cssId{s80}{1}\cr &\quad\cssId{s81}{\text{addition property of inequality}}\cr\cr &\cssId{s82}{x}\cssId{s83}{\gt} \cssId{s84}{-\frac 12}\cr &\quad\cssId{s85}{\text{divide by a negative #; reverse inequality}} \end{align} $$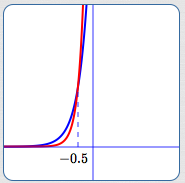
Blue curve:
$y = 2^{3x - 1}$
Red curve:
$y = 2^{5x}$
Blue curve lies below
red curve for $\,x \gt -\frac 12$
Example 2
Solve: $\displaystyle\frac 1{3^{x^2-1}} > 1$
This inequality will be solved in two different ways. As long as you use correct tools in a correct way, there are often different ways you can proceed.
Solution #1:
$$ \begin{align} &\cssId{s96}{\frac 1{3^{x^2-1}}}\cssId{s97}{\gt}\ \cssId{s98}{1}\cr &\quad\cssId{s99}{\text{original inequality}}\cr\cr &\cssId{s100}{\left(\frac 13\right)^{x^2-1}}\cssId{s101}{\gt}\cssId{s102}{\left(\frac 13\right)^0}\cr &\quad\cssId{s103}{\text{rename both sides using exponent laws}}\cr\cr &\cssId{s104}{x^2 - 1}\cssId{s105}{\lt} \cssId{s106}{0}\cr &\quad\cssId{s107}{\text{use (2); inequality changes direction}}\cr\cr &\cssId{s108}{x^2}\cssId{s109}{\lt} \cssId{s110}{1}\cr &\quad\cssId{s111}{\text{addition property of inequality}}\cr\cr &\cssId{s112}{-1} \cssId{s113}{\lt}\cssId{s114}{x} \cssId{s115}{\lt} \cssId{s116}{1}\cr &\quad\cssId{s117}{\text{inspection (knowledge of $x^2$ curve)}} \end{align} $$Solution #2:
$$ \begin{align} &\cssId{s119}{\frac 1{3^{x^2-1}}}\cssId{s120}{\gt} \ \cssId{s121}{1}\cr &\quad\cssId{s122}{\text{original inequality}}\cr\cr &\cssId{s123}{1}\cssId{s124}{\gt}\cssId{s125}{3^{x^2-1}}\cr &\quad\cssId{s126}{\text{multiply both sides by $3^{x^2-1}\overset{\text{always}}{\gt}0$}}\cr\cr &\cssId{s127}{3^0} \cssId{s128}{\gt}\cssId{s129}{3^{x^2-1}}\cr &\quad\cssId{s130}{\text{rename: $1 = 3^0$}}\cr\cr &\cssId{s131}{0}\cssId{s132}{\gt}\ \cssId{s133}{x^2 - 1}\cr &\quad\cssId{s134}{\text{use (1)}}\cr\cr &\cssId{s135}{x^2}\cssId{s136}{\lt}\cssId{s137}{1}\cr &\quad\cssId{s138}{\text{addition property; re-arrange}}\cr\cr &\cssId{s139}{-1} \cssId{s140}{\lt}\cssId{s141}{x}\cssId{s142}{\lt} \cssId{s143}{1}\cr &\quad\cssId{s144}{\text{inspection (knowledge of $x^2$ curve)}} \end{align} $$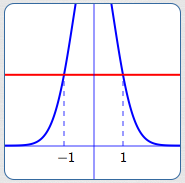
Blue curve:
$\displaystyle y = \frac{1}{3^{x^2-1}}$
Red curve:
$y = 1$
Blue curve
lies above red curve
for $\,x\,$ between $\,-1\,$ and $\,1\,$