More on Exterior Angles in Triangles

Exterior angles in polygons were studied in an earlier section, Interior and Exterior Angles in Polygons.
This section reviews and extends previous results, focusing only on exterior angles in triangles.

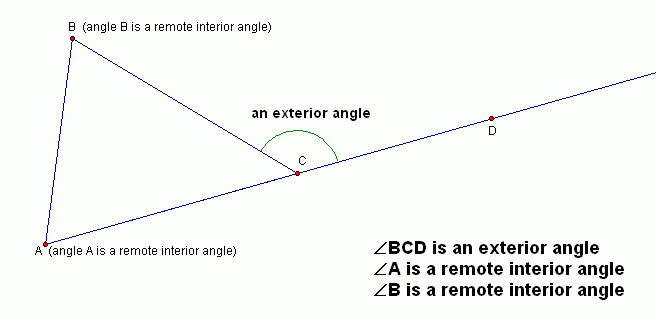
If you extend a side in a triangle, then a linear pair automatically appears.
One of the angles in the linear pair is an angle in the triangle, and its supplement is called an exterior angle of the triangle.
The two angles in the triangle that are not involved in this linear pair are called the remote interior angles with respect to the exterior angle.

Notice, of course, that exterior angles are outside a triangle, and remote interior angles are inside a triangle.

Here is a precise definition:

DEFINITIONS exterior angle of a triangle; remote interior angles

An exterior angle of a triangle is an angle that forms a linear pair with an angle of the triangle.

If a triangle has angles

$\,\angle A\,$, $\,\angle B\,$, and $\,\angle C\,$,
and if we focus attention on an exterior angle at

$\,\angle C\,$,
then $\,\angle A\,$ and $\,\angle B\,$ are called the remote interior angles with respect to $\,\angle C\,$.

An exterior angle has a beautiful relationship to its remote interior angles, as discussed next.

Let $\,\Delta ABC\,$ be a triangle.
Extend side $\,\overline{AC}\,$ to obtain an exterior angle where $\,\angle A\,$ and $\,\angle B\,$ are the remote interior angles,
and let $\,\angle E\,$ denote the exterior angle (see below).

Since $\,\angle BCA\,$ and $\,\angle E\,$ are supplements, $\,m\angle BCA +m\angle E = 180^{\circ}\,$.

Since the angles in a triangle sum to $\,180^{\circ}\,$, $\,m\angle BCA + m\angle A + m\angle B = 180^{\circ}\,$.

A little bit of algebra then shows that $\,m\angle E = m\angle A+m\angle B\,$.

Thus, we have proved the following:

EXTERIOR ANGLE THEOREM

The measure of an exterior angle of a triangle is equal to
the sum of the measures of its remote interior angles.

Since an angle in a triangle has strictly positive measure,
it follows immediately that an exterior angle must be strictly greater than either remote interior angle: $$ m\angle E = m\angle A + m\angle B \gt m\angle A\ \ \ \ \ \text{ and }\ \ \ \ \ m\angle E = m\angle A + m\angle B \gt m\angle B $$

This result is stated as a corollary to the previous theorem:

COROLLARY

The measure of an exterior angle of a triangle is greater than
the measure of either remote interior angle.

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Parallel Lines

(MAX is 12; there are 12 different problem types.)