 Relationships Between Angles and Sides in Triangles
Relationships Between Angles and Sides in Triangles
You may want to review:
In a triangle, we can often use information about the lengths of sides to gain information about the measures of angles. Or, we can use information about the measures of angles to gain information about the lengths of sides.
This section explores notation and results that relate the angles and sides in triangles.
First, recall the biconditional statement: to prove a sentence of the form $\,A\Longleftrightarrow B\,,$ one can prove both the forward direction $\,A\Rightarrow B\,$ and the reverse direction $\,A\Leftarrow B\,$ (that is, $\,B\Rightarrow A\,$). Together, this proves the equivalence.
The justification is the truth table below, which shows that $\,A\Longleftrightarrow B\,$ is equivalent to $(A\Rightarrow B) \text{ and } (B\Rightarrow A)\,.$ Notice that the last two columns are identical!
| $A$ | $B$ | $A\Rightarrow B$ | $B\Rightarrow A$ | $(A\Rightarrow B)$ and $(B\Rightarrow A)$ | $A\Longleftrightarrow B$ |
| T | T | T | T | T | T |
| T | F | F | T | F | F |
| F | T | T | F | F | F |
| F | F | T | T | T | T |
The biconditional statement is used below to prove our first result relating sides and angles: if two sides in a triangle have the same length, then the opposite angles have the same measure. And, if two angles in a triangle have the same measure, then the opposite sides have the same lengths.
Notice what a beautiful application of SAS and ASA congruence the proof is. It's a simple and clever idea—showing that a triangle is congruent to a ‘flipped’ copy of itself.
|
GIVEN:
PROVE: |
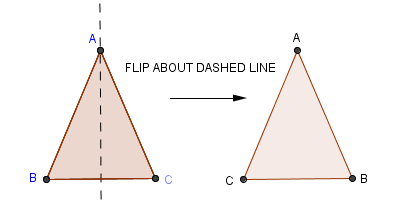
|
| PROOF #1: | |
| STATEMENTS | REASONS |
| 1. $\,AB=AC\,$ | given |
| 2. $\,AC=AB\,$ | given |
| 3. $\,m\angle A=m\angle A\,$ | reflexive property (equality is an equivalence relation on the set of real numbers) |
| 4. $\,\Delta ABC\cong \Delta ACB\,$ | SAS |
| 5. $\,m\angle B=m\angle C\,$ | CPCTC |
|
GIVEN:
PROVE: |

|
| PROOF #2: | |
| STATEMENTS | REASONS |
| 1. $\,m\angle B=m\angle C\,$ | given |
| 2. $\,m\angle C=m\angle B\,$ | given |
| 3. $\,BC=CB\,$ | reflexive property (equality is an equivalence relation on the set of real numbers) |
| 4. $\,\Delta ABC\cong \Delta ACB\,$ | ASA |
| 5. $\,AB=AC\,$ | CPCTC |
Together, we have:
Two sides of a triangle have equal lengths
$\ \Longleftrightarrow \ $
the angles opposite them have equal measures.
Proof
‘$\,\Rightarrow \,$’
See Proof #1 above.
‘$\,\Leftarrow \,$’
See Proof #2 above.
Q.E.D.
Note: ‘Q.E.D’ is an abbreviation for the Latin phrase ‘quod erat demonstrandum’ which means ‘that which was to be demonstrated (proved).’ It is often used to mark the end of a proof.
A triangle is equilateral if and only if all its sides are equal.
A triangle is isosceles if and only if it has at least two equal sides.
A triangle is scalene if and only if all its sides have different lengths.
Recall that since the angles in a triangle sum to $\,180^{\circ}\,,$ a triangle can have at most one obtuse angle.
The name theorem in mathematics is usually reserved for important results. Things that don't seem quite worthy of being called ‘theorems’ are often given other names. In particular, a corollary is usually an interesting consequence of a theorem.
Here's a corollary to the previous theorem:
Every equilateral triangle is equiangular.
Every equiangular triangle is equilateral.
The proof is left to the reader.
Finally, while we're on the subject of angles and sides in a triangle, here's an interesting and useful theorem:
- the longest side is opposite the biggest angle
- the medium side is opposite the medium angle
- the shortest side is opposite the smallest angle