More Terminology for Segments and Angles

Due to math content, this page has special requirements (including JavaScript) for full functionality.
With your current viewing scenario, it is not appearing and behaving as it is supposed to!
Please visit Dr. Carol J.V. Fisher's Homepage to learn what this site has to offer.
Watch the "Welcome" video to get started—hope to see you back here soon!

Dr. Carol J.V. Fisher's Homepage

For this exercise, you need ♥ INTERNET EXPLORER 6.0 and above, with MathPlayer installed.♥

MORE TERMINOLOGY FOR SEGMENTS AND ANGLES

Jump right to the exercises!

Harold R. Jacobs has written a great Geometry book, entitled Geometry: Seeing, Doing, Understanding, third edition.
It has many excellent exercises.
The notation used here for betweenness of points is the same notation that is used by Jacobs.

Any line can be "transformed" into a number line by choosing locations for zero (0) and one (1).
With these choices, the positions of all other real numbers are uniquely determined.

A number line is a conceptually perfect picture of the real numbers:
each point on the line corresponds to a unique real number,
and each real number corresponds to a unique point on the line.

When points are located on a number line, it is convenient to use the following convention:
The coordinate of point A is denoted by a .
The coordinate of point B is denoted by b .
Thus, uppercase letters are used to denote points,
and the corresponding lowercase letter is used to denote the coordinate of the point.
In Geometry, you want to be careful to distinguish between a point (an exact location),
and a number (that might be used to specify the location of the point, relative to a chosen coordinate system).

Recall that, given any two real numbers x and y , we can talk about the distance between them:

If x>y , then the distance between them is x-y .
If x<y , then the distance between them is y-x .
A general formula for the distance between x and y is | y-x | (or | x-y | ).

That is, to find the distance between any two real numbers, subtract them (in any order) and then take the absolute value.

The distance between points A and B is the length of the segment AB&bar; , and will be denoted by AB (no overline).
Thus, AB&bar; is a geometric figure (a line segment), but AB is a number that specifies the length of the line segment AB&bar; .

Given three points on a line, it is often convenient to talk about one of the points being between the other two:

DEFINITION: BETWEENNESS OF POINTS
Let A, B, and C be three points on a line, with corresponding coordinates a, b and c.
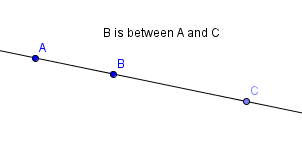
We say that B is between A and C if and only if ( a<b<c    or     a>b>c ) .

The sentence " B is between A and C " will be notated by either A-B-C or C-B-A .
Notice that whenever B is between A and C , then BA + BC = AC .

Recall that ∠AVB denotes the angle with vertex V , point A on one side, and point B on the other side.
As discussed earlier, angles can be measured with a protractor. Often, angles are measured in degrees.
The notation m∠AVB is used to denote the measure of ∠AVB .
Thus, ∠AVB is a geometric figure (an angle), but m∠AVB is a number (that measures how "wide" the angle is).

Angles are classified according to their size:

DEFINITION: ANGLE CLASSIFICATIONS
An angle is acute if and only if its measure is strictly between 0° and 90°.
An angle is a right angle if and only if its measure is 90°.
An angle is obtuse if and only if its measure is strictly between 90° and 180°.
An angle is a straight angle if and only if its measure is 180°.

Two geometric figures are said to be congruent if they coincide exactly when superimposed, one on the other.
For segments and angles, we can decide if they are congruent by looking at their measures:
Line segments are congruent if and only if they have the same lengths.
Angles are congruent if and only if they have the same measures.

On this exercise, you will not key in your answer.
However, you can check to see if your answer is correct.